作业3:LetNet 网络实现
作业3:LeNet 网络实现报告
LeNet-5 网络模型作为卷积神经网络中的开创性工作,提出了三大思想:
-
局部感知
-
权值共享
-
下采样
因为图像特征分布在图像的像素上,利用卷积操作可以在多个位置提取相类似的特征,于是有了局部感知。另外由于当年并没有计算能力强悍的 GPU 来辅助训练神经网络,因此通过下采样层有效地加快训练和提取更高维特征,能够节省参数和计算,这与当年的技术相比是一个关键的优势。另外原论文中提到,全卷积不应该被放在第一层,图像特征有着高度的空间相关性,因此权值共享可以充分利用图像上的空间相关性。
1. LeNet 网络介绍
手写字体识别模型 LeNet-5 诞生于 1998 年,是最早的卷积神经网络之一。LeNet-5 通过巧妙的设计,利用卷积、参数共享、池化等操作提取特征,避免了大量的计算成本,最后再使用全连接神经网络进行分类识别,这个网络也是最近大量神经网络架构的起点。LeNet-5 的网络结构如图所示。
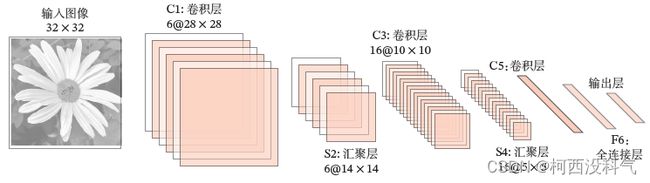
LeNet-5 共有 7 层,接受输入图像大小为 32*32=1024,输出对应10个类别的得分。LetNet-5 中的每一层结构如下:
-
C1 层是卷积层,使用 6 个
5*5的卷积核,得到 6 组大小为28*28=784的特征映射。因此,C1 层的神经元数量为6*784=4704,可训练参数数量为6*25+6=156,连接数为156*784=122304(包括偏置在内)。 -
S2 层为汇聚层,采样窗口为
2*2,使用平均汇聚,神经元个数为6*14*14=1176,可训练参数数量为6*(1+1)=12,连接数为6*196*(4+1)=5880。 -
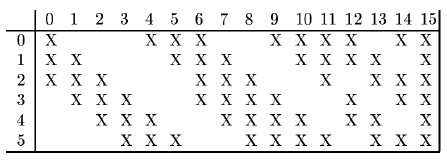
C3 层为卷积层,LeNet-5 中用一个连接表来定义输入和输出特征映射之间的依赖关系,共使用 60 个
5*5的卷积核,得到 16 组大小为10*10的特征映射。神经元数量为16*100=1600,可训练参数数量为(60*25)+16=1516,连接数为100*1516=151600。卷积层的每一个输出特征映射都依赖于所有输入特征映射,相当于卷积层的输入和输出特征映射之间是全连接的关系。实际上,这种全连接关系不是必须的。可以让每一个输出特征映射都依赖于少数几个输入特征映射。定义一个连接表(Link Table)T 来描述输入和输出特征映射之间的连接关系。在 LeNet-5 中,连接表的基本设定如下图所示。C3 层的第 0-5 个特征映射依赖于 S2 层的特征映射组的每 3 个连续子集,第 6-11 个特征映射依赖于 S2 层的特征映射组的每 4 个连续子集,第 12-14 个特征映射依赖于 S2 层的特征映射的每 4 个不连续子集,第 15 个特征映射依赖于 S2 层的所有特征映射。
-
S4 层是一个汇聚层,由 16 个
5*5大小的特征图构成。特征图中的每个单元与 C3 中相应特征图的2*2邻域相连接,跟 C1 和 S2 之间的连接一样。S4 层有 32 个可训练参数(每个特征图 1 个因子和一个偏置)和 2000 个连接。 -
C5 层是一个卷积层,有 120 个特征图。每个单元与 S4 层的全部 16 个单元的
5*5邻域相连。由于 S4 层特征图的大小也为5*5(同滤波器一样),故 C5 特征图的大小为1*1,这构成了 S4 和 C5 之间的全连接。之所以仍将 C5 标示为卷积层而非全相联层,是因为如果 LeNet-5 的输入变大,而其他的保持不变,那么此时特征图的维数就会比1*1大。C5 层有120*(16*25+1)=48120个可训练连接。 -
F6 层是一个全连接层,有 84 个神经元,与C5层全相连。可训练参数数量为
84*(120+1)=10164。连接数和可训练参数个数相同,为 10164。如同经典神经网络,F6 层计算输入向量和权重向量之间的点积,再加上一个偏置。然后将其传递给sigmoid函数产生单元i的一个状态。 -
输出层:输出层由 10 个径向基函数(Radial Basis Function,RBF)组成。每类一个单元,每个有 84 个输入。每个输出 RBF 单元计算输入向量和参数向量之间的欧式距离。输入离参数向量越远,RBF 输出的越大。一个 RBF 输出可以被理解为衡量输入模式和与 RBF 相关联类的一个模型的匹配程度的惩罚项。用概率术语来说,RBF 输出可以被理解为 F6 层配置空间的高斯分布的负
log-likelihood。给定一个输入模式,损失函数应能使得 F6 的配置与 RBF 参数向量(即模式的期望分类)足够接近。这些单元的参数是人工选取并保持固定的(至少初始时候如此)。这些参数向量的成分被设为 -1 或1。虽然这些参数可以以 -1 和 1 等概率的方式任选,或者构成一个纠错码,但是被设计成一个相应字符类的7*12大小(即 84)的格式化图片。这种表示对识别单独的数字不是很有用,但是对识别可打印 ASCII 集中的字符串很有用。使用这种分布编码而非更常用
1 of N编码用于产生输出的另一个原因是,当类别比较大的时候,非分布编码的效果比较差。原因是大多数时间非分布编码的输出必须为 0。这使得用sigmoid单元很难实现。另一个原因是分类器不仅用于识别字母,也用于拒绝非字母。使用分布编码的 RBF 更适合该目标。因为与sigmoid不同,他们在输入空间的较好限制的区域内兴奋,而非典型模式更容易落到外边。RBF 参数向量起着 F6 层目标向量的角色。需要指出这些向量的成分是 +1 或 -1,这正好在 F6
sigmoid的范围内,因此可以防止sigmoid函数饱和。实际上,+1 和 -1 是sigmoid函数的最大弯曲的点处。这使得 F6 单元运行在最大非线性范围内。必须避免sigmoid函数的饱和,因为这将会导致损失函数较慢的收敛和病态问题。
2. 实现效果
3. 代码实现
总共代码一共包含 3 个文件,分别是模型文件 LeNet5.py、模型训练文件 LeNet5_Train.py、以及测试文件 LeNet5_Test.py。数据集来自 kaggle。
依赖环境:
- python3
- PyTorch
- pandas
- matplotlib
- numpy
3.1. 模型代码
对应 LeNet5.py 文件,包含一个卷积层和池化层,分别对应 LeNet5 中的 C1 和 S2。卷积层的输入通道为 1,输出通道为 6,设置卷积核大小 5*5,步长为 1。池化层的 kernel 大小为 2*2 。最后定义了反向传播函数。
关键代码:
class LeNet5(nn.Module):
def __init__(self):
super(LeNet5, self).__init__()
self._conv1 = nn.Sequential(nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5, stride=1), nn.MaxPool2d(kernel_size=2))
self._conv2 = nn.Sequential(nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1),nn.MaxPool2d(kernel_size=2))
self._fc1 = nn.Sequential(nn.Linear(in_features=4*4*16, out_features=120))
self._fc2 = nn.Sequential(nn.Linear(in_features=120, out_features=84))
self._fc3 = nn.Sequential(nn.Linear(in_features=84, out_features=10))
def forward(self, input):
conv1_output = self._conv1(input)
conv2_output = self._conv2(conv1_output)
conv2_output = conv2_output.view(-1, 4 * 4 * 16)
fc1_output = self._fc1(conv2_output)
fc2_output = self._fc2(fc1_output)
fc3_output = self._fc3(fc2_output)
return fc3_output
3.2. 模型训练代码
对应 LeNet5_Train.py 文件,代码使用了交叉熵损失函数,SGD 优化算法,设置学习率为 0.001,动量设置为0.9,小批量数据集大小设置为 30,迭代次数为 1000 次。
关键代码:
for i in range(1000):
batch_data = train_data.sample(n=30, replace=False)
batch_y = torch.from_numpy(batch_data.iloc[:,0].values).long()
batch_x = torch.from_numpy(batch_data.iloc[:,1::].values).float().view(-1,1,28,28)
prediction = model.forward(batch_x)
loss = loss_fc(prediction, batch_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
print("第%d次训练,loss为%.3f" % (i, loss.item()))
loss_list.append(loss)
x.append(i)
plt.figure()
plt.xlabel("number of epochs")
plt.ylabel("loss")
plt.plot(x,loss_list,"r-")
plt.show()
可以看到大概经过 30 次训练之后,损失就已经降到一个较低的水平了。
3.3. 模型测试代码
对应 LeNet5_Train.py 文件,总共进行了 100 次测试,每次测试从测试集中随机挑选 50 个样本,然后计算网络的识别准确率。
关键代码:
for i in range(100):
batch_data = test_data.sample(n=50,replace=False)
batch_x = torch.from_numpy(batch_data.iloc[:,1::].values).float().view(-1,1,28,28)
batch_y = batch_data.iloc[:,0].values
prediction = np.argmax(model(batch_x).numpy(), axis=1)
acccurcy = np.mean(prediction==batch_y)
print("第%d组测试集,准确率为%.3f" % (i,acccurcy))
accuracy_list.append(acccurcy)
testList.append(i)
plt.figure()
plt.xlabel("number of tests")
plt.ylabel("accuracy rate")
plt.ylim(0,1)
plt.plot(testList, accuracy_list,"r-")
plt.legend()
plt.show()
平均准确率在 96% 左右。
4. 总结
-
LeNet-5 是一种用于手写体字符识别的非常高效的卷积神经网络。
-
卷积神经网络能够很好的利用图像的结构信息。
-
卷积层的参数较少,这也是由卷积层的主要特性即局部连接和共享权重所决定。


