JAVA算法：子集求和问题（Subset Sum Problem）

JAVA算法：子集求和问题（Subset Sum Problem）

题目：给定一个正整数数组，和一个目标值，找出是否存在数组的一个子数组，使得子数组元素之和等于目标值。

例如：给定数组 { 3, 2, 7, 1} 和目标值 S = 6

返回结果： True ， 子数组为 (3, 2, 1}

问题分析：

使用递归算法和动态规划算法两种算法来求解上述问题。

递归算法

对于数组中的每个元素有两个选择，我们在子数组中包括该元素和在子数组中不包括该元素。

在给定的例子中：数组 { 3, 2, 7, 1} 和目标值 S = 6

如果我们考虑另一个数组A，它也包括4个元素（数组A和给定的数组具有相同的长度）
如果数组A中包括原数组的元素，则数组A的元素设置为1（对应于原数组元素的下标位置）；否则设置为0

这样，我们需要找到每一个可能的子集，并且检查是否子集的元素之和等于目标值。 

package com.bean.algorithm.dp;

public class SubSetSumRecursion {
	public static void find(int[] A, int currSum, int index, int sum, int[] solution) {
		if (currSum == sum) {
			System.out.println("\nSum found");
			for (int i = 0; i < solution.length; i++) {
				if (solution[i] == 1) {
					System.out.print("  " + A[i]);
				}
			}

		} else if (index == A.length) {
			return;
		} else {
			solution[index] = 1;// select the element
			currSum += A[index];
			find(A, currSum, index + 1, sum, solution);
			currSum -= A[index];
			solution[index] = 0;// do not select the element
			find(A, currSum, index + 1, sum, solution);
		}
		return;
	}

	public static void main(String[] args) {
		int[] A = { 3, 2, 7, 1 };
		int[] solution = new int[A.length];
		find(A, 0, 0, 6, solution);
	}
}

程序运行结果：

Sum found
  3  2  1

---

动态规划算法

Base Cases：

• If no elements in the set then we can’t make any subset except for 0.
• If sum needed is 0 then by returning the empty subset we can make the subset with sum 0.

Given – Set = arrA[], Size = n, sum = S

• Now for every element in he set we have 2 options, either we include it or exclude it.
• for any ith element-
• If include it => S = S-arrA[i], n=n-1
• If exclude it => S, n=n-1.

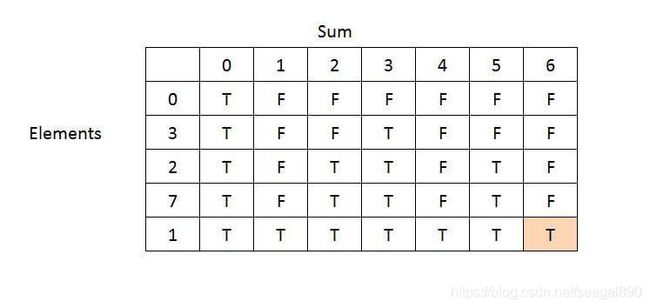
状态方程推导：

Recursive Equation:
Base Cases:
SubsetSum(arrA, n, S)= false, if sum > 0 and n == 0 SubsetSum(arrA, n, S)= true, if sum == 0 (return empty set)
Rest Cases
SubsetSum(arrA, n, S) = SubsetSum(arrA, n-1, S)|| SubsetSum(arrA, n-1, S-arrA[n-1])

推算过程 

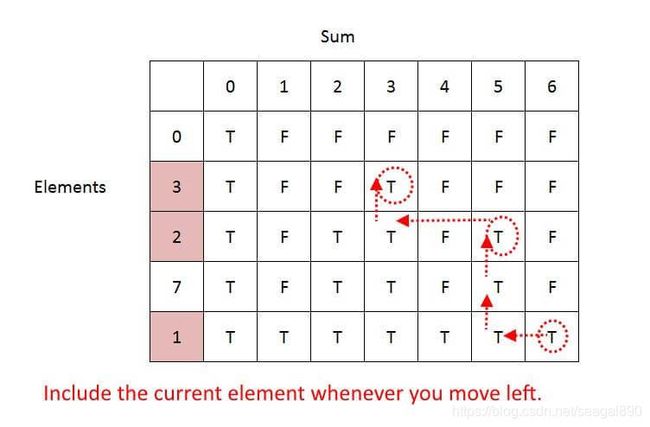
如何跟踪元素。

从右下角开始，然后回溯，从True开始检查。

如果上面单元格中的值为 false，则表示当前单元格在包含当前元素后变为 true。

因此，包括当前元素并检查 sum=sum–current元素。

 

package com.bean.algorithm.dp;

public class SubsetSumProblem {

	public static boolean subSetDP(int[] A, int sum) {
		boolean[][] solution = new boolean[A.length + 1][sum + 1];
		// if sum is not zero and subset is 0, we can't make it
		for (int i = 1; i <= sum; i++) {
			solution[0][i] = false;
		}
		// if sum is 0 the we can make the empty subset to make sum 0
		for (int i = 0; i <= A.length; i++) {
			solution[i][0] = true;
		}
		//
		for (int i = 1; i <= A.length; i++) {
			for (int j = 1; j <= sum; j++) {
				// first copy the data from the top
				solution[i][j] = solution[i - 1][j];

				// If solution[i][j]==false check if can be made
				if (solution[i][j] == false && j >= A[i - 1])
					solution[i][j] = solution[i][j] || solution[i - 1][j - A[i - 1]];
			}
		}
		return solution[A.length][sum];
	}

	public static void main(String[] args) {
		int[] A = { 3, 2, 7, 1 };
		System.out.println("\nFrom DP: " + subSetDP(A, 6));
	}
}

程序运行结果：

From DP: true

表示存在子数组之和等于目标值。