snow_wang13804

LTE物理层概述（6）-- LTE之调制与解调及其matlab仿真

LTE（长期演进）下行链路 PHY（物理）层处理链路可以认为是下行链路共享信道（DLSCH）和物理下行链路共享信道（PDSCH）处理的组合。DLSCH 即下行链路传输信道 TrCH。

LTE下行链路物理模型描述，具体可参照之前文章：

LTE物理层概述（3）-- 下行链路物理模型概述https://blog.csdn.net/snowman898/article/details/124684077

本节主要学习 LTE物理信道的调制与解调功能，文末给出仿真代码。

1、调制

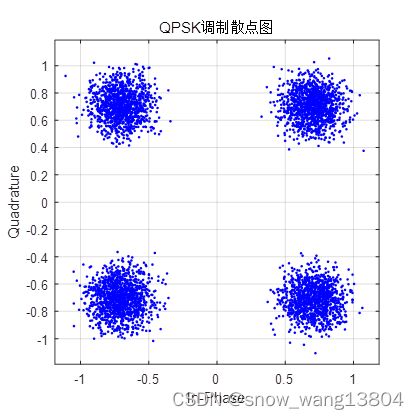
LTE使用的调制方案包括：QPSK, QAM16 和 QAM64。图1所示为三个调制方案的星座图：

图1 LTE 三种调制方案星座图

1.1 QPSK调制器映射规则

表1 LTE中QPSK调制映射器规则
载荷比特图形	调制符号
	同相（I）	正交（Q）
00	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$
01	$\frac{1}{\sqrt{2}}$	$-\frac{1}{\sqrt{2}}$
10	$-\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$
11	$-\frac{1}{\sqrt{2}}$	$-\frac{1}{\sqrt{2}}$

1.2 QAM16 调制器映射规则

表2 LTE中QAM16调制映射器规则
载荷比特图形	调制符号		载荷比特图形	调制符号
载荷比特图形	同相（I）	正交（Q）	载荷比特图形	同相（I）	正交（Q）
0000	$\frac{1}{\sqrt{10}}$	$\frac{1}{\sqrt{10}}$	1000	$-\frac{1}{\sqrt{10}}$	$\frac{1}{\sqrt{10}}$
0001	$\frac{1}{\sqrt{10}}$	$\frac{3}{\sqrt{10}}$	1001	$-\frac{1}{\sqrt{10}}$	$\frac{3}{\sqrt{10}}$
0010	$\frac{3}{\sqrt{10}}$	$\frac{1}{\sqrt{10}}$	1010	$-\frac{3}{\sqrt{10}}$	$\frac{1}{\sqrt{10}}$
0011	$\frac{3}{\sqrt{10}}$	$\frac{3}{\sqrt{10}}$	1011	$-\frac{3}{\sqrt{10}}$	$\frac{3}{\sqrt{10}}$
0100	$\frac{1}{\sqrt{10}}$	$-\frac{1}{\sqrt{10}}$	1100	$-\frac{1}{\sqrt{10}}$	$-\frac{1}{\sqrt{10}}$
0101	$\frac{1}{\sqrt{10}}$	$-\frac{3}{\sqrt{10}}$	1101	$-\frac{1}{\sqrt{10}}$	$-\frac{3}{\sqrt{10}}$
0110	$\frac{3}{\sqrt{10}}$	$-\frac{1}{\sqrt{10}}$	1110	$-\frac{3}{\sqrt{10}}$	$-\frac{1}{\sqrt{10}}$
0111	$\frac{3}{\sqrt{10}}$	$-\frac{3}{\sqrt{10}}$	1111	$-\frac{3}{\sqrt{10}}$	$-\frac{3}{\sqrt{10}}$

1.3 QAM64 调制器映射规则

表3 LTE中QAM64调制映射器规则
载荷比特图形	调制符号		载荷比特图形	调制符号
载荷比特图形	同相（I）	正交（Q）	载荷比特图形	同相（I）	正交（Q）
000000	$\frac{3}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$	100000	$-\frac{3}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$
000001	$\frac{3}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$	100001	$-\frac{3}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$
000010	$\frac{1}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$	100010	$-\frac{1}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$
000011	$\frac{1}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$	100011	$-\frac{1}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$
000100	$\frac{3}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$	100100	$-\frac{3}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$
000101	$\frac{3}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$	100101	$-\frac{3}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$
000110	$\frac{1}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$	100110	$-\frac{1}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$
000111	$\frac{1}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$	100111	$-\frac{1}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$
001000	$\frac{5}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$	101000	$-\frac{5}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$
001001	$\frac{5}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$	101001	$-\frac{5}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$
001010	$\frac{7}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$	101010	$-\frac{7}{\sqrt{42}}$	$\frac{3}{\sqrt{42}}$
001011	$\frac{7}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$	101011	$-\frac{7}{\sqrt{42}}$	$\frac{1}{\sqrt{42}}$
001100	$\frac{5}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$	101100	$-\frac{5}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$
001101	$\frac{5}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$	101101	$-\frac{5}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$
001110	$\frac{7}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$	101110	$-\frac{7}{\sqrt{42}}$	$\frac{5}{\sqrt{42}}$
001111	$\frac{7}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$	101111	$-\frac{7}{\sqrt{42}}$	$\frac{7}{\sqrt{42}}$
010000	$\frac{3}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$	110000	$-\frac{3}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$
010001	$\frac{3}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$	110001	$-\frac{3}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$
010010	$\frac{1}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$	110010	$-\frac{1}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$
010011	$\frac{1}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$	110011	$-\frac{1}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$
010100	$\frac{3}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$	110100	$-\frac{3}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$
010101	$\frac{3}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$	110101	$-\frac{3}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$
010110	$\frac{1}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$	110110	$-\frac{1}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$
010111	$\frac{1}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$	110111	$-\frac{1}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$
011000	$\frac{5}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$	111000	$-\frac{5}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$
011001	$\frac{5}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$	111001	$-\frac{5}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$
011010	$\frac{7}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$	111010	$-\frac{7}{\sqrt{42}}$	$-\frac{3}{\sqrt{42}}$
011011	$\frac{7}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$	111011	$-\frac{7}{\sqrt{42}}$	$-\frac{1}{\sqrt{42}}$
011100	$\frac{5}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$	111100	$-\frac{5}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$
011101	$\frac{5}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$	111101	$-\frac{5}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$
011110	$\frac{7}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$	111110	$-\frac{7}{\sqrt{42}}$	$-\frac{5}{\sqrt{42}}$
011111	$\frac{7}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$	111111	$-\frac{7}{\sqrt{42}}$	$-\frac{7}{\sqrt{42}}$

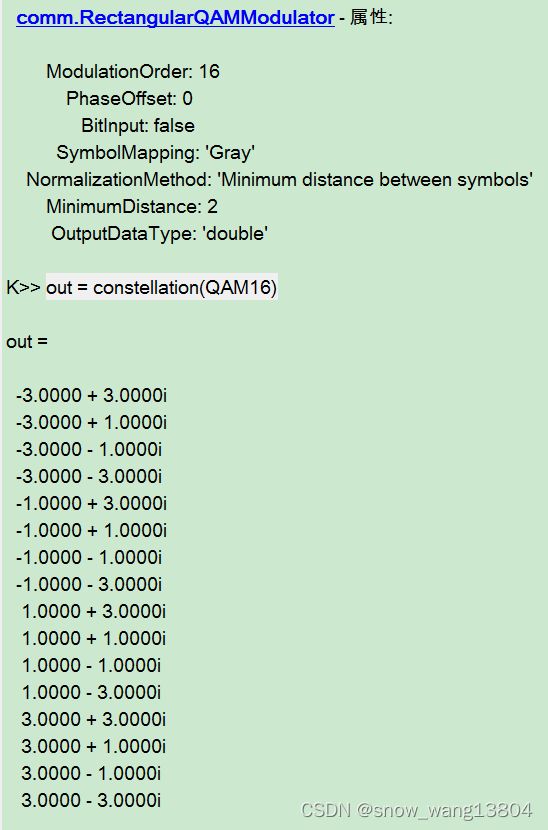
在实际实现中，尤其是matlab，我们可以调用以下代码：

QAM16 = comm.RectangularQAMModulator(16);
out = constellation(QAM16);

2、Matlab实现

function y = lte_Modulator(u, Mode)

% Initialization
% Mode 1 -- QPSK 2--
%%
% 为避免每次调用函数时创建和释放系统对象的开销，函数内的系统对象为持久变量声明类型
%  持久变量声明类型可以支持只在函数第一次调用时创建系统对象，从而提高循环调用函数时的仿真速度
%%

persistent QPSK QAM16 QAM64
if isempty(QPSK)
    QPSK = comm.PSKModulator(4, 'BitInput', true, 'PhaseOffset', pi/4,...
                  'SymbolMapping', 'Custom', 'CustomSymbolMapping', [0 2 3 1]);
              
    QAM16 = comm.RectangularQAMModulator(16, 'BitInput', true, 'NormalizationMethod', 'Average power',...
                  'SymbolMapping', 'Custom', 'CustomSymbolMapping', [11 10 14 15 9 8 12 13 1 0 4 5 3 2 6 7]);
              
    QAM64 = comm.RectangularQAMModulator(64, 'BitInput', true, 'NormalizationMethod', 'Average power',...
                  'SymbolMapping', 'Custom', 'CustomSymbolMapping',...
                   [47 46 42 43 59 58 62 63 45 44 40 41 57 56 60 61 37 36 32 33 49 ...
                    48 52 53 39 38 34 35 51 50 54 55 7 6 2 3 19 18 22 23 5 4 0 1 ...
                   17 16 20 21 13 12 8 9 25 24 28 29 15 14 10 11 27 26 30 31]);
end

% Processing
switch Mode
    case 1
        y = step(QPSK, u);
    case 2
        y = step(QAM16,u);
    case 3
        y = step(QAM64,u);
end

2.1 LTE调制Matlab实现

在QPSK调制情况下，我们可以调用 comm.PSKModulator 系统对象并将其调制阶数设置为4.参数属性描述如下：

1）' BitInput ' 属性：这里设置属性为 ' true' , 表示将调制器输入为比特值向量。QPSK调制下，每 2bit 映射到一个调制符号；

2） ' PhaseOffset ' 属性：这里设置为 pi / 4，表示调制符号对应复平面单位圆上4个点，角度依

次为 [ 3/4 pi, pi / 4, -pi / 4, -3 / 4 pi ]；

3）' CustomSymbolMapping ' 属性：确保LTE中定义的比特图形产生相应的输出符号。

对于QAM16，QAM64调制实现，可参考如上代码利用matlab通信工具箱函数实现。

2.2 LTE解调及Matlab实现

解调可以使用硬判决或者软判决解码 —— 使用硬判决解码时，解调器输入符号映射为估计输出比特；软判决解码时，输出为对数估计似然比（LLR）向量。

硬判决解调代码如下所示：

function y = lte_DemodulatorHard(u, Mode)

% Initialization
% Mode 1 -- QPSK 2--
persistent QPSK QAM16 QAM64
if isempty(QPSK)
    QPSK = comm.PSKDemodulator('ModulationOrder',4, 'BitOutput', true, ...
           'PhaseOffset',pi/4,'SymbolMapping', 'Custom', 'CustomSymbolMapping',  ...
           [0 2 3 1]);
              
    QAM16 = comm.RectangularQAMDemodulator('ModulationOrder',16, 'BitOutput', true, ...
       'NormalizationMethod', 'Average power','SymbolMapping', 'Custom', ...
       'CustomSymbolMapping', [11 10 14 15 9 8 12 13 1 0 4 5 3 2 6 7]);
              
    QAM64 = comm.RectangularQAMDemodulator('ModulationOrder',64, 'BitOutput', true, ...
            'NormalizationMethod', 'Average power','SymbolMapping', 'Custom', ...
            'CustomSymbolMapping', [47 46 42 43 59 58 62 63 45 44 40 41 ...
            57 56 60 61 37 36 32 33 49 48 52 53 39 38 34 35 51 50 54 55 7 6 2 3 19 18 ... 
            22 23 5 4 0 1 17 16 20 21 13 12 8 9 25 24 28 29 15 14 10 11 27 26 30 31]);
end

软判决解调代码如下所示

function y = lte_DemodulatorSoft(u, Mode, NoiseVar)

% Initialization
% Mode 1 -- QPSK 2--
persistent QPSK QAM16 QAM64

if isempty(QPSK)
    QPSK = comm.PSKDemodulator('ModulationOrder',4, 'BitOutput', true,   ...
              'PhaseOffset',pi/4, 'SymbolMapping', 'Custom',   ...
              'CustomSymbolMapping', [0 2 3 1], 'DecisionMethod', ...
              'Approximate log-likelihood ratio', 'VarianceSource', 'Input port');
              
    QAM16 = comm.RectangularQAMDemodulator('ModulationOrder',16, 'BitOutput', true,  ...
              'NormalizationMethod', 'Average power', 'SymbolMapping', 'Custom', ... 
              'CustomSymbolMapping', [11 10 14 15 9 8 12 13 1 0 4 5 3 2 6 7], ...
              'DecisionMethod', 'Approximate log-likelihood ratio', ...
              'VarianceSource', 'Input port');
              
    QAM64 = comm.RectangularQAMDemodulator('ModulationOrder',64, 'BitOutput', true, ... 
              'NormalizationMethod', 'Average power', 'SymbolMapping', ...
              'Custom','CustomSymbolMapping', [47 46 42 43 59 58 62 63 45 44 40 41 ...
              57 56 60 61 37 36 32 33 49 48 52 53 39 38 34 35 51 50 54 55 7 6 2 3 19 ...
              22 23 5 4 0 1  17 16 20 21 13 12 8 9 25 24 28 29 15 14 10 11 27 26 30 31], 
              'DecisionMethod', 'Approximate log-likelihood ratio', ...
              'VarianceSource', 'Input port');
end

2.3 BER测量

QAM16和 QAM64 的带宽利用率分别是 QPSK 的 2倍和3倍。不过，高阶调制方案会更易受到信道噪声的影响。比较QPSK、QAM16和QAM64调制方案，在给定误码率概率下，接收端需要更高的Eb/No。

以下代码为一个简单的LTE 调制解调系统，用以衡量各种调制方案的BER和SNR之间的关系。该系统包括调制器、解调器、AWGN信道、计算BER和Eb/No的函数。主要代码展示如下所示：


clear
clc
close all

EbNo = 25;
maxNumErrs = 1000;
maxNumBits = 20e6;

FRM = 9600;
% Modulation Mode 
ModulationMode =3;          % 1--QPSK  2--QAM16  3-- QAM64
k = 2* ModulationMode;
snr = EbNo + 10*log10(k);   

% Processing loop: transmitter, channel model and receiver
 numErrs = 0;
 numBits = 0;
 
 AWGN = comm.AWGNChannel;
 AWGN.EbNo = snr;
 
 while((numErrs < maxNumErrs) && (numBits < maxNumBits))
    
     % Transmitter
    u = randi([0,1], FRM, 1);
    x = lte_Modulator( u, ModulationMode);
        
    % channel
    c0 = AWGN.step(x);
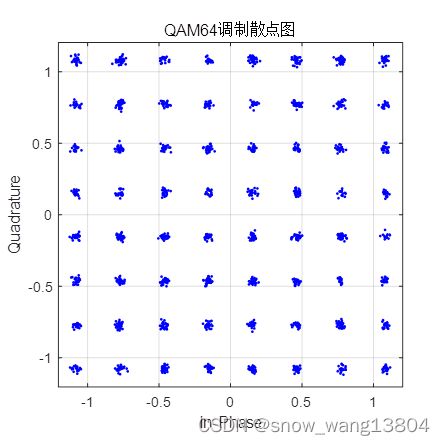
    c1 = scatterplot(c0);
    title('QAM64调制散点图');
    grid on
    
    % Receiver
    r0 = lte_DemodulatorHard(c0, ModulationMode);
    y = r0(1:FRM);
    
    % Measurements 
    numErrs = numErrs + sum(y ~= u);
    numBits = numBits + FRM;
 end
 
 %
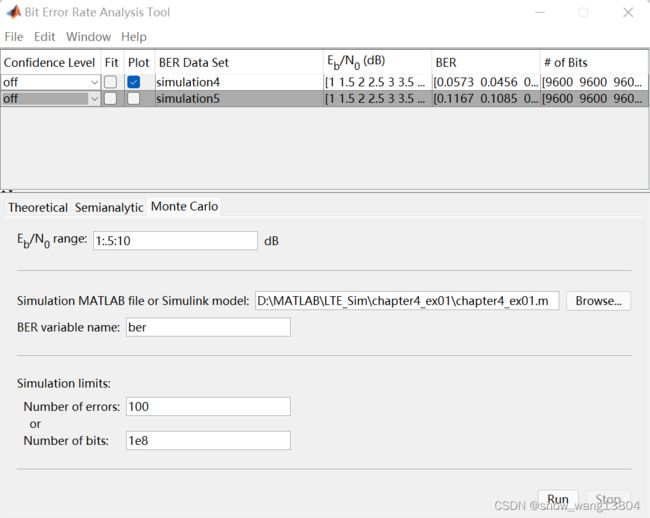
 ber = numErrs / numBits

由于该仿真以函数形式呈现，实际执行时要调用MATLAB工具箱 bertool

配置好后，分别将 “ chapter1_ex01.m”代码中：

% Modulation Mode
ModulationMode =3; % 1--QPSK 2--QAM16 3-- QAM64

ModulationMode值设置为1,2,3，从而得到各种调制方式下 EbNo 与 ber的关系图：

本系统完整代码资源可下载：

LTE QPSK、QAM16 以及 QAM64调制下 EbNo 与误码率BER之间的仿真关系图https://download.csdn.net/download/snowman898/85372067

说明：本章所述原理，只为让大家有系统的认识，可以完整了解 LTE 调制信号链路。以下再补充2点：

1）关于QAM16/64具体的数学公式推导，大家可以自行搜索，个人推荐以下帖子：

QAM信号的调制解调原理https://blog.csdn.net/gemengxia/article/details/116150246?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522165249485116782391887600%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=165249485116782391887600&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_positive~default-1-116150246-null-null.142^v9^control,157^v4^control&utm_term=qam%E8%B0%83%E5%88%B6&spm=1018.2226.3001.4187

2）QAM16以及QAM64关键技术实现及其难点，后续会另开帖子说明。

情绪觉察日记第37天露露_e800
今天是家庭关系规划师的第二阶最后一天，慧萍老师帮我做了个案，帮我处理了埋在心底好多年的一份恐惧，并给了我深深的力量！这几天出来学习，爸妈过来婆家帮我带小孩，妈妈出于爱帮我收拾东西，并跟我先生和婆婆产生矛盾，妈妈觉得他们没有照顾好我…。今晚回家见到妈妈，我很欣赏她并赞扬她，妈妈说今晚要跟我睡我说好，当我们俩躺在床上准备睡觉的时候，我握着妈妈的手对她说:妈妈这几天辛苦你了，你看你多利害把我们的家收拾得
机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
铭刻于星（四十二）随风至
69夜晚，绍敏同学做完功课后，看了眼房外，没听到动静才敢从书包的夹层里拿出那个心形纸团。折痕压得很深，都有些旧了，想来是已经写好很久了。绍敏同学慢慢地、轻轻地捏开折叠处，待到全部拆开后，又反复抚平纸张，然后仔细地一字字默看。只是开头的三个字是第一次看到，让她心漏跳了几拍。“亲爱的绍敏：从四年级的时候，我就喜欢你了，但是我一直不敢说，怕影响你学习。六年级的时候听说有人跟你表白，你接受了，我很难过，但
UI学习——cell的复用和自定义cell Magnetic_h ui 学习
目录cell的复用手动（非注册）自动（注册）自定义cellcell的复用在iOS开发中，单元格复用是一种提高表格（UITableView）和集合视图（UICollectionView）滚动性能的技术。当一个UITableViewCell或UICollectionViewCell首次需要显示时，如果没有可复用的单元格，则视图会创建一个新的单元格。一旦这个单元格滚动出屏幕，它就不会被销毁。相反，它被添
学点心理知识，呵护孩子健康静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所，超越教育与技术的思考》的讲座。今天又重新学习了一遍，收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题，她说心理健康的一些基本命题，我们与我们通常的一些教育命题是不同的，她还举了几个例子，让我们明白我们原来以为的健康并非心理学上的健康。比如如果
ArcGIS栅格计算器常见公式（赋值、0和空值的转换、补充栅格空值）研学随笔 arcgis 经验分享
我们在使用ArcGIS时通常经常用到栅格计算器，今天主要给大家介绍我日常中经常用到的几个公式，供大家参考学习。将特定值（-9999）赋值为0，例如-9999.Con("raster"==-9999,0,"raster")2.给空值赋予特定的值（如0）Con(IsNull("raster"),0,"raster")3.将特定的栅格值(如1)赋值为空值，其他保留原值SetNull("raster"==
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
回溯 Leetcode 332 重新安排行程 mmaerd Leetcode刷题学习记录 leetcode 算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets，其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK（肯尼迪国际机场）出发的先生，所以该行程必须从JFK开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。例如，行程[“JFK”,“LGA”]与[“JFK”,“LGB
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
2019-12-22-22:30 涓涓1016
今天是冬至，写下我的日更，是因为这两天的学习真的是能量的满满，让我看到了自己，未来另外一种可能性，也让我看到了这两年这几年的过程中我所接受那些痛苦的来源。一切的根源和痛苦都来自于人生，家庭，而你的原生家庭，你的爸爸和妈妈，是因为你这个灵魂在那一刻选择他们作为你的爸爸和妈妈来的，所以你得接受他，你得接纳他，他就是因为他的存在而给你的学习和成长带来这些痛苦，那其实是你必然要经历的这个过程，当你去接纳的
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
2023-04-17|篮球女孩长一木
1小学抑或初中阶段，在课外书了解到她的故事。“篮球女孩”。当时佩服她的顽强，也对生命多了一丝敬畏。今天刚好在公众号看到，长大后的“篮球女孩”。佩服之余又满是心疼。网络侵删祝那素未蒙面的女孩，未来一切顺遂。
在一台Ubuntu计算机上构建Hyperledger Fabric网络落叶无声9 区块链超级账本 Hyperledger fabric 区块链 ubuntu 构建 hyperledger fabric
在一台Ubuntu计算机上构建HyperledgerFabric网络Hyperledgerfabric是一个开源的区块链应用程序平台，为开发基于区块链的应用程序提供了一个起点。当我们提到HyperledgerFabric网络时，我们指的是使用HyperledgerFabric的正在运行的系统。即使只使用最少数量的组件，部署Fabric网络也不是一件容易的事。Fabric社区创建了一个名为Cello
GitHub上克隆项目 bigbig猩猩 github
从GitHub上克隆项目是一个简单且直接的过程，它允许你将远程仓库中的项目复制到你的本地计算机上，以便进行进一步的开发、测试或学习。以下是一个详细的步骤指南，帮助你从GitHub上克隆项目。一、准备工作1.安装Git在克隆GitHub项目之前，你需要在你的计算机上安装Git工具。Git是一个开源的分布式版本控制系统，用于跟踪和管理代码变更。你可以从Git的官方网站（https://git-scm.
HTML网页设计制作大作业（div+css）云南我的家乡旅游景点带文字滚动二挡起步 web前端期末大作业 web设计网页规划与设计 html css javascript dreamweaver 前端
Web前端开发技术描述网页设计题材，DIV+CSS布局制作,HTML+CSS网页设计期末课程大作业游景点介绍|旅游风景区|家乡介绍|等网站的设计与制作HTML期末大学生网页设计作业HTML：结构CSS：样式在操作方面上运用了html5和css3，采用了div+css结构、表单、超链接、浮动、绝对定位、相对定位、字体样式、引用视频等基础知识JavaScript：做与用户的交互行为文章目录前端学习路线
Day17笔记-高阶函数 ~在杰难逃~ Python 笔记 python 开发语言 pycharm 数据分析
高阶函数【重点掌握】函数的本质：函数是一个变量，函数名是一个变量名，一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数，B函数调用完成之后，会得到一个结果，则B函数被称为高阶函数常用的高阶函数：map(),reduce(),filter(),sorted()1.map()map(func,iterable)，返回值是一个iterator【容器，迭代器】func:函数iterab
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
人工智能时代，程序员如何保持核心竞争力？ jmoych 人工智能
随着AIGC（如chatgpt、midjourney、claude等）大语言模型接二连三的涌现，AI辅助编程工具日益普及，程序员的工作方式正在发生深刻变革。有人担心AI可能取代部分编程工作，也有人认为AI是提高效率的得力助手。面对这一趋势,程序员应该如何应对?是专注于某个领域深耕细作，还是广泛学习以适应快速变化的技术环境?又或者，我们是否应该将重点转向AI无法轻易替代的软技能？让我们一起探讨程序员
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
node.js学习小猿L node.js node.js 学习 vim
node.js学习实操及笔记温故node.js，node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础，三大框架vuereactangular离不开node.jsnode.js是什么官网：node.js是一个开源的、跨平台的运行JavaScript的运行
阶段总结反思轻争
马上就要进入10月份了，今天做一下前段时间的总结和反思。前段时间，日更、英语、健身、护肤坚持的比较好。阅读、书法坚持的不好。1.中间被迫停更半个多月，其余时间一直在坚持日更挑战。偶尔也有不想写的时候，就做一下摘抄。因为阅读（输入）没跟上来，所以写作（输出）质量有待进一步加强。2.英语做到了一周至少学习5天，每次不少于30分钟，但是小班课没有跟上更新速度，下一步要争取利用零碎时间补听小班课。3.减肥
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
【华为OD技术面试真题 - 技术面】-测试八股文真题题库（1）算法大师华为od 面试 python 算法前端
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.黑盒测试和白盒测试的区别2.假设我们公司现在开发一个类似于微信的软件1.0版本，现在要你测试这个功能：打开聊天窗口，输入文本，限制字数在200字以内。问你怎么提取测试点。功能测试性能测试安全性测试可用性测试跨平台兼容性测试网络环境测试3.接口测试的工具你了解哪些
ARM驱动学习之基础小知识 JT灬新一 ARM 嵌入式 arm开发学习
ARM驱动学习之基础小知识•sch原理图工程师工作内容–方案–元器件选型–采购（能不能买到，价格）–原理图（涉及到稳定性）•layout画板工程师–layout（封装、布局，布线，log）（涉及到稳定性）–焊接的一部分工作（调试阶段板子的焊接）•驱动工程师–驱动，原理图，layout三部分的交集容易发生矛盾•PCB研发流程介绍–方案，原理图(网表)–layout工程师（gerber文件）–PCB板
ARM驱动学习之5 LEDS驱动 JT灬新一嵌入式 C 底层 arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点：•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点：DRIVER_NAME和DEVICE_NAME匹配。实现步骤：1.加入需要的头文件：//Linux平台的gpio头文件#include//三
ARM驱动学习之4小结 JT灬新一嵌入式 C++arm开发学习 linux
ARM驱动学习之4小结#include#include#include#include#include#defineDEVICE_NAME"hello_ctl123"MODULE_LICENSE("DualBSD/GPL");MODULE_AUTHOR("TOPEET");staticlonghello_ioctl(structfile*file,unsignedintcmd,unsignedlo
jQuery 跨域访问的三种方式 No 'Access-Control-Allow-Origin' header is present on the reque qiaolevip 每天进步一点点学习永无止境跨域众观千象
XMLHttpRequest cannot load http://v.xxx.com. No 'Access-Control-Allow-Origin' header is present on the requested resource. Origin 'http://localhost:63342' is therefore not allowed access. test.html:1
mysql 分区查询优化 annan211 java 分区优化 mysql
分区查询优化引入分区可以给查询带来一定的优势，但同时也会引入一些bug. 分区最大的优点就是优化器可以根据分区函数来过滤掉一些分区，通过分区过滤可以让查询扫描更少的数据。所以，对于访问分区表来说，很重要的一点是要在where 条件中带入分区，让优化器过滤掉无需访问的分区。可以通过查看explain执行计划，是否携带 partitions
MYSQL存储过程中使用游标 chicony Mysql存储过程
DELIMITER $$ DROP PROCEDURE IF EXISTS getUserInfo $$ CREATE PROCEDURE getUserInfo(in date_day datetime)-- -- 实例-- 存储过程名为：getUserInfo-- 参数为：date_day日期格式:2008-03-08-- BEGINdecla
mysql 和 sqlite 区别 Array_06 sqlite
转载： http://www.cnblogs.com/ygm900/p/3460663.html mysql 和 sqlite 区别 SQLITE是单机数据库。功能简约，小型化，追求最大磁盘效率 MYSQL是完善的服务器数据库。功能全面，综合化，追求最大并发效率 MYSQL、Sybase、Oracle等这些都是试用于服务器数据量大功能多需要安装，例如网站访问量比较大的。而sq
pinyin4j使用 oloz pinyin4j
首先需要pinyin4j的jar包支持；jar包已上传至附件内方法一:把汉字转换为拼音；例如：编程转换后则为biancheng /** * 将汉字转换为全拼 * @param src 你的需要转换的汉字 * @param isUPPERCASE 是否转换为大写的拼音； true:转换为大写；fal
微博发送私信随意而生微博
在前面文章中说了如和获取登陆时候所需要的cookie，现在只要拿到最后登陆所需要的cookie，然后抓包分析一下微博私信发送界面 http://weibo.com/message/history?uid=****&name=**** 可以发现其发送提交的Post请求和其中的数据，让后用程序模拟发送POST请求中的数据，带着cookie发送到私信的接入口，就可以实现发私信的功能了。
jsp 香水浓 jsp
JSP初始化容器载入JSP文件后，它会在为请求提供任何服务前调用jspInit()方法。如果您需要执行自定义的JSP初始化任务，复写jspInit()方法就行了 JSP执行这一阶段描述了JSP生命周期中一切与请求相关的交互行为，直到被销毁。当JSP网页完成初始化后
在 Windows 上安装 SVN Subversion 服务端 AdyZhang SVN
在 Windows 上安装 SVN Subversion 服务端2009-09-16高宏伟哈尔滨市道里区通达街291号最佳阅读效果请访问原地址：http://blog.donews.com/dukejoe/archive/2009/09/16/1560917.aspx 现在的Subversion已经足够稳定，而且已经进入了它的黄金时段。我们看到大量的项目都在使
android开发中如何使用 alertDialog从listView中删除数据？ aijuans android
我现在使用listView展示了很多的配置信息，我现在想在点击其中一条的时候填出 alertDialog,点击确认后就删除该条数据，（ ArrayAdapter ，ArrayList，listView 全部删除），我知道在下面的onItemLongClick 方法中参数 arg2 是选中的序号，但是我不知道如何继续处理下去 1 2 3
jdk-6u26-linux-x64.bin 安装 baalwolf linux
1.上传安装文件(jdk-6u26-linux-x64.bin) 2.修改权限 [root@localhost ~]# ls -l /usr/local/jdk-6u26-linux-x64.bin 3.执行安装文件 [root@localhost ~]# cd /usr/local [root@localhost local]# ./jdk-6u26-linux-x64.bin&nbs
MongoDB经典面试题集锦 BigBird2012 mongodb
1.什么是NoSQL数据库？NoSQL和RDBMS有什么区别？在哪些情况下使用和不使用NoSQL数据库？ NoSQL是非关系型数据库，NoSQL = Not Only SQL。关系型数据库采用的结构化的数据，NoSQL采用的是键值对的方式存储数据。在处理非结构化/半结构化的大数据时；在水平方向上进行扩展时；随时应对动态增加的数据项时可以优先考虑使用NoSQL数据库。在考虑数据库的成熟
JavaScript异步编程Promise模式的6个特性 bijian1013 JavaScript Promise
Promise是一个非常有价值的构造器，能够帮助你避免使用镶套匿名方法，而使用更具有可读性的方式组装异步代码。这里我们将介绍6个最简单的特性。在我们开始正式介绍之前，我们想看看Javascript Promise的样子： var p = new Promise(function(r
[Zookeeper学习笔记之八]Zookeeper源代码分析之Zookeeper.ZKWatchManager bit1129 zookeeper
ClientWatchManager接口 //接口的唯一方法materialize用于确定那些Watcher需要被通知 //确定Watcher需要三方面的因素1.事件状态 2.事件类型 3.znode的path public interface ClientWatchManager { /** * Return a set of watchers that should
【Scala十五】Scala核心九：隐式转换之二 bit1129 scala
隐式转换存在的必要性，在Java Swing中，按钮点击事件的处理，转换为Scala的的写法如下： val button = new JButton button.addActionListener( new ActionListener { def actionPerformed(event: ActionEvent) {
Android JSON数据的解析与封装小Demo ronin47
转自：http://www.open-open.com/lib/view/open1420529336406.html package com.example.jsondemo; import org.json.JSONArray; import org.json.JSONException; import org.json.JSONObject; impor
[设计]字体创意设计方法谈 brotherlamp UI ui自学 ui视频 ui教程 ui资料
从古至今，文字在我们的生活中是必不可少的事物，我们不能想象没有文字的世界将会是怎样。在平面设计中，UI设计师在文字上所花的心思和功夫最多，因为文字能直观地表达UI设计师所的意念。在文字上的创造设计，直接反映出平面作品的主题。如设计一幅戴尔笔记本电脑的广告海报，假设海报上没有出现“戴尔”两个文字，即使放上所有戴尔笔记本电脑的图片都不能让人们得知这些电脑是什么品牌。只要写上“戴尔笔
单调队列-用一个长度为k的窗在整数数列上移动，求窗里面所包含的数的最大值 bylijinnan java 算法面试题
import java.util.LinkedList; /* 单调队列滑动窗口单调队列是这样的一个队列：队列里面的元素是有序的，是递增或者递减题目：给定一个长度为N的整数数列a(i),i=0,1,...,N-1和窗长度k. 要求：f(i) = max{a(i-k+1),a(i-k+2),..., a(i)},i = 0,1,...,N-1 问题的另一种描述就
struts2处理一个form多个submit chiangfai struts2
web应用中，为完成不同工作，一个jsp的form标签可能有多个submit。如下代码： <s:form action="submit" method="post" namespace="/my"> <s:textfield name="msg" label="叙述：">
shell查找上个月，陷阱及野路子 chenchao051 shell
date -d "-1 month" +%F 以上这段代码，假如在2012/10/31执行，结果并不会出现你预计的9月份，而是会出现八月份，原因是10月份有31天，9月份30天，所以-1 month在10月份看来要减去31天，所以直接到了8月31日这天，这不靠谱。野路子解决：假设当天日期大于15号
mysql导出数据中文乱码问题 daizj mysql 中文乱码导数据
解决mysql导入导出数据乱码问题方法：１、进入mysql，通过如下命令查看数据库编码方式： mysql> show variables like 'character_set_%'; +--------------------------+----------------------------------------+ | Variable_name&nbs
SAE部署Smarty出现：Uncaught exception 'SmartyException' with message 'unable to write dcj3sjt126com PHP smarty sae
对于SAE出现的问题：Uncaught exception 'SmartyException' with message 'unable to write file...。官方给出了详细的FAQ：http://sae.sina.com.cn/?m=faqs&catId=11#show_213 解决方案为： 01 $path
《教父》系列台词 dcj3sjt126com
Your love is also your weak point. 你的所爱同时也是你的弱点。 If anything in this life is certain, if history has taught us anything, it is that you can kill anyone. 不顾家的人永远不可能成为一个真正的男人。 &
mongodb安装与使用 dyy_gusi mongo
一.MongoDB安装和启动,widndows和linux基本相同 1.下载数据库, linux:mongodb-linux-x86_64-ubuntu1404-3.0.3.tgz 2.解压文件,并且放置到合适的位置 tar -vxf mongodb-linux-x86_64-ubun
Git排除目录 geeksun git
在Git的版本控制中，可能有些文件是不需要加入控制的，那我们在提交代码时就需要忽略这些文件，下面讲讲应该怎么给Git配置一些忽略规则。有三种方法可以忽略掉这些文件，这三种方法都能达到目的，只不过适用情景不一样。 1. 针对单一工程排除文件这种方式会让这个工程的所有修改者在克隆代码的同时，也能克隆到过滤规则，而不用自己再写一份，这就能保证所有修改者应用的都是同一
Ubuntu 创建开机自启动脚本的方法 hongtoushizi ubuntu
转载自： http://rongjih.blog.163.com/blog/static/33574461201111504843245/ Ubuntu 创建开机自启动脚本的步骤如下： 1) 将你的启动脚本复制到 /etc/init.d目录下以下假设你的脚本文件名为 test。 2) 设置脚本文件的权限 $ sudo chmod 755
第八章流量复制/AB测试/协程 jinnianshilongnian nginx lua coroutine
流量复制在实际开发中经常涉及到项目的升级，而该升级不能简单的上线就完事了，需要验证该升级是否兼容老的上线，因此可能需要并行运行两个项目一段时间进行数据比对和校验，待没问题后再进行上线。这其实就需要进行流量复制，把流量复制到其他服务器上，一种方式是使用如tcpcopy引流；另外我们还可以使用nginx的HttpLuaModule模块中的ngx.location.capture_multi进行并发
电商系统商品表设计 lkl
DROP TABLE IF EXISTS `category`; -- 类目表 /*!40101 SET @saved_cs_client = @@character_set_client */; /*!40101 SET character_set_client = utf8 */; CREATE TABLE `category` ( `id` int(11) NOT NUL
修改phpMyAdmin导入SQL文件的大小限制 pda158 sql mysql
　用phpMyAdmin导入mysql数据库时，我的10M的数据库不能导入，提示mysql数据库最大只能导入2M。　　 phpMyAdmin数据库导入出错：　　You probably tried to upload too large file. Please refer to documentation for ways to workaround this limit.
Tomcat性能调优方案 Sobfist apache jvm tomcat 应用服务器
一、操作系统调优对于操作系统优化来说，是尽可能的增大可使用的内存容量、提高CPU的频率，保证文件系统的读写速率等。经过压力测试验证，在并发连接很多的情况下，CPU的处理能力越强，系统运行速度越快。。【适用场景】任何项目。二、Java虚拟机调优应该选择SUN的JVM，在满足项目需要的前提下，尽量选用版本较高的JVM，一般来说高版本产品在速度和效率上比低版本会有改进。 J
SQLServer学习笔记 vipbooks 数据结构 xml
1、create database school 创建数据库school 2、drop database school 删除数据库school 3、use school 连接到school数据库，使其成为当前数据库 4、create table class(classID int primary key identity not null) 创建一个名为class的表，其有一