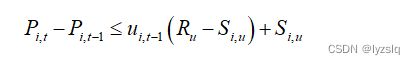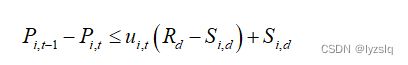基于MATLAB/yalmip/cplex 的机组最优组合
文章目录
- 一、绪论
-
- 1.研究目的
- 2.背景概述
- 二、机组组合优化数学模型
-
- 2.1.问题分析
- 2.2.符号说明
- 2.3.模型建立
- 2.4.模型简化
- 三、算例介绍
- 总结
一、绪论
1.研究目的
(1).熟练掌握MATLAB及CPLEX的使用。
(2).初步了解优化问题的基本形式和求解方法。
(3).掌握对既定数学模型进行编程求解的能力。
(4).掌握运用Cplex解决电力系统机组组合(含经济调度)问题的方法。
2.背景概述
MATLAB是是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,是科研中不可缺少的建模工具。
IBM CPLEX ILOG是IBM公司开发的优化引擎,可用于求解大规模数学规划问题。通过在MATLAB中调用CPLEX工具箱,就能方便地利用MATLAB平台进行模型的求解,并为模型文件提供了求解、分析、操作及写入/读出的方法。同时通过引入Yalmip工具箱,能够大大简化程序格式,提高程序可读性。
为了实现电力供需的平衡,并最合理地利用发电资源,预先对发电机组的启停和出力进行调度安排就是非常必要的,这就是机组组合问题(Unit Commitment, UC)。机组组合问题问题是一类混合整数规划问题(Mixed Integer Programming, MIP),能过通过MATLAB/CPLEX得到求解。
评注:现在做电力系统优化最主流的方法就是Matlabp+CPlex(含Yalmip)
二、机组组合优化数学模型
2.1.问题分析
机组组合问题要求基于已知的系统数据,求解计划时间内机组决策变量的最优组合,使得系统总成本达到最小。该问题的决策变量由两类,一类是各时段机组的启停状态,为整数变量,0表示关停,1表示启动;另一类是各时段机组的出力,为连续变量。
机组组合问题属于规划问题,即要在决策变量的可行解空间里找到一组最优解,使得目标函数尽可能取得极值。对于混合整数规划,常用的方法有分支定界法,benders分解等。CPLEX提供了快速的MIP求解方法,对于数学模型已知的问题,只需要按照程序规范在MATLAB中编写程序化模型,调用CPLEX求解器,即可进行求解。
下文介绍机组组合优化的数学模型。
2.2.符号说明
2.3.模型建立
根据上述变量定义,建立含安全约束的机组最优组合(SCUC)模型如下:
1)目标函数
目标函数即为最小化成本,包括发电带来的煤耗成本和机组启停产生的开停机成本。

其中,机组的煤耗函数可用出力的二次函数表述:
2)等式约束条件
此即为系统的功率平衡约束

3)不等式约束条件
a)热备用约束

b)机组出力约束
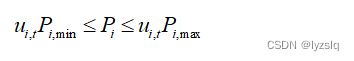
c)机组爬坡约束

d)机组起停时间约束

e)起停费用约束
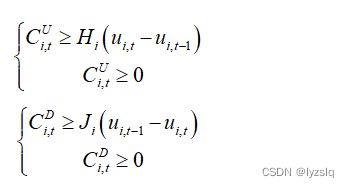
f)潮流安全约束
当机组启动最小出力大于爬坡速率,约束将使得所有关停的机组都无法启动,因此改写为

计算潮流的转移分布因子矩阵,将改写为

其中描述节点i的注入功率对于线路l产生的影响。则简化模型的变量为和,在满足-,-的约束下,最小化目标函数。(转移分布因子矩阵计算较为繁琐,开始时可先忽略此约束)
2.4.模型简化
由上小节构建的机组组合优化模型,煤耗成本采用二次函数,当系统规模较大时(如节点数超过1000),求解起来将消耗大量时间。因此我们可以对原模型进行线性化处理。
将煤耗函数分段线性化,分为m段,将原模型的替换为

其中,代表分段线性化后煤耗函数各段斜率,表示机组开机并以最小出力运行产生的煤耗,为机组分段的出力,满足

三、算例介绍
校验程序的算例基于IEEE-30节点标准测试系统,系统接线图如图1。系统包30个节点,6台发电机组。要求确定系统最优机组组合,使得系统各机组总运行成本(煤耗成本+启停成本)最小化。

已知:给定系统数据包括如下:
1)线路网络参数
2)机组参数
3)各节点各时段负荷曲线(24小时)
注意:附件中的数据均基于标幺化系统得到,因此电力电量参数、网络参数等都为标幺值,无量纲。还要注意附件中煤耗系数a,b,c的单位为吨,因此计算煤耗成本还需换算为价格,设燃煤价格为100$/吨。
求解:机组组合结果,即机组各时段启停计划、机组各时段最优出力,以及内含的各时段的直流潮流等。
系统参数部分代码如下(示例):
%% 系统参数
%所有参数均用有名值表示
paragen=xlsread('~~~','机组参数');
loadcurve=xlsread('~~~','负荷曲线');
netpara=xlsread('~~~','网络参数');
branch_num=size(netpara);%网络中的支路
branch_num=branch_num(1,1);
PL_max=netpara(:,6);%线路最大负荷
PL_min=netpara(:,7);%线路最小负荷
limit=paragen(:,3:4);%机组出力上下限//limit(:,1)表示上限,limit(:,2)表示下限
para=paragen(:,5:7);%成本系数//para(:,1)表示系数a,para(:,2)表示系数b,para(:,3)表示系数c。
price=100;
para=price*para;%价格换算
lasttime=paragen(:,9);%持续时间
Rud=paragen(:,8);%上下爬坡速率//因题中简化上坡下坡速度相同
H=paragen(:,10);%启动成本
J=paragen(:,11);%关停成本
u0=[1 1 1 1 1 1];%初始状态
%% 规模变量
%机组数
gennum=size(paragen);
gennum=gennum(1,1);
%节点数
numnodes=size(loadcurve);
numnodes=numnodes(1,1)-1;
%时间范围
T=size(loadcurve);
T=T(1,2)-1;
%线性化分段数(按需要更改)
m=4;
%各时刻节点总负荷
PL=loadcurve(numnodes+1,2:T+1);
%%
%决策变量
u=binvar(gennum,T,'full');%状态变量
p=sdpvar(gennum,T,'full');%即各机组实时功率p(i,t)
Ps=sdpvar(gennum,T,m,'full');%分段出力
costH=sdpvar(gennum,T,'full');%启动成本
costJ=sdpvar(gennum,T,'full');%关停成本
sum_PowerGSDF=sdpvar(T,branch_num,numnodes,'full');%发电机的输出功率转移总和
求解部分代码如下(示例):
%% 求解
ops=sdpsettings('solver', 'cplex');
result=solvesdp(st,totalcost);
总结
以上就是今天要讲基于MATLAB/yalmip/cplex 的机组最优组合的内容,本文仅仅简单介绍了yalmip/cplex两个求解器的使用,代码在我的资源可找。