OpenCV47:理解KNN|k-Nearest Neighbour

目标

在本章中，将理解

• k最近邻（kNN）算法的概念

理论

kNN是可用于监督学习的最简单的分类算法之一。这个想法是在特征空间中搜索测试数据的最近邻。用下面的图片来研究它。

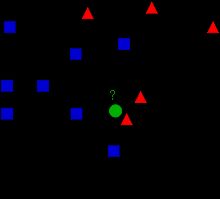
在图像中，有两个族类，蓝色正方形和红色三角形。称每一种为类（Class）。他们的房屋显示在他们的城镇地图中，我们称之为特征空间（ Feature Space）。 （可以将特征空间视为投影所有数据的空间。例如，考虑一个2D坐标空间。每个数据都有两个特征，x和y坐标。可以在2D坐标空间中表示此数据；如果有三个特征，则需要3D空间；现在考虑N个特征，需要N维空间，这个N维空间就是其特征空间。在上图中，可以将其视为2D情况。有两个特征）。
现在有一个新成员进入城镇并创建了一个新房屋，显示为绿色圆圈。它应该被添加到这些蓝色/红色家族之一中。称该过程为分类（Classification）。这个新会员应该如何分类？本文使用kNN算法解决上述问题。

一种方法是检查谁是其最近邻。从图像中可以明显看出它是红色三角形家族。因此，它也被添加到了红色三角形中。此方法简称为最近邻（Nearest Neighbour ）分类，因为分类仅取决于最近邻。
但这是有问题的。红三角可能是最近的。但是，如果附近有很多蓝色方块怎么办？然后，蓝色方块在该地区的权重比红色三角更大。因此，仅检查最接近的一个是不够的。相反，检查一些k个近邻的族。那么，看谁占多数，新样本就属于那个类。在上图中，假设设置k=3，即3个最近族。它有两个红色和一个蓝色（有两个等距的蓝色，但是由于k = 3，只取其中一个），所以它应该加入红色家族。但是，如果我们取k=7时，它有5个蓝色族和2个红色族，它应该加入蓝色族。因此，分类结果随着k的值而变化。更有趣的是，如果k=4时，它有2个红色邻居和2个蓝色邻居，这是一个平局！因此最好将k设置为奇数。由于分类取决
于k个最近的邻居，因此该方法称为k近邻。
同样，在kNN中，在考虑k个邻居时，对所有人都给予同等的重视，这公平吗？例如，以k=4的情况为例，按照数量来说这是平局。但是其中的两个红色族比其他两个蓝色族离它更近。因此，它更应该被添加到红色。那么如何用数学解释呢？根据每个家庭到新来者的距离来给他们一些权重。对于那些靠近它的人，权重增加，而那些远离它的人，权重减轻。
然后，分别添加每个族的总权重。谁得到的总权重最高，新样本归为那一族。这称为modified kNN或者** weighted kNN**。
因此，使用kNN算法时候，需要了解的重要信息如下：

• 需要了解镇上所有房屋的信息，因为必须检查新样本到所有现有房屋的距离，以找到最近的邻居。如果有许多房屋和家庭，则需要大量的内存，并且需要更多的时间进行计算
• 任何类型的“训练”或准备几乎是零时间。“学习”涉及在测试和分类之前记住（存储）数据

OpenCV中的kNN

就像上面一样，将在这里做一个简单的例子，有两个族（类）。
因此，在这里，将红色系列标记为Class-0（用0表示），将蓝色系列标记为Class-1（用1表示）。创建25个族或25个训练数据，并将它们标记为0类或1类。借助Numpy中的Random Number Generator来完成所有这些工作。然后在Matplotlib的帮助下对其进行绘制。红色系列显示为红色三角形，蓝色系列显示为蓝色正方形。

import cv2
import numpy as np
from matplotlib import pyplot as plt

# Feature set containing (x,y) values of 25 known/training data
trainData = np.random.randint(0, 100, (25, 2)).astype(np.float32)

# Label each one either Red or Blue with numbers 0 and 1
responses = np.random.randint(0, 2, (25, 1)).astype(np.float32)
responses

# Take Red neighbours and plot them
red = trainData[responses.ravel()==0]
plt.scatter(red[:, 0], red[:, 1], 80, 'r', '^')

# Take Blue neighbours and plot them
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:, 0], blue[:, 1], 80, 'b', 's')

plt.show()

由于使用的是随机数生成器，因此每次运行代码都将获得不同的数据。
接下来启动kNN算法，并传递trainData和响应以训练kNN（它会构建搜索树）。
然后，将在OpenCV中的kNN的帮助下将一个新样本进行分类。在进入kNN之
前，需要了解测试数据（新样本数据）上的知识。数据应为浮点数组，其大小为$numberoftestdata\times numberoffeatures$。然后找到新加入的最近邻。可以指定我们想要多少个邻居k（这里设置为3）。它返回：

• 给新样本的标签取决于kNN理论。如果要使用“最近邻居”算法，只需指定k=1即可，其中k是邻居数
• k最近邻的标签
• 与新邻居的新距离相应的距离

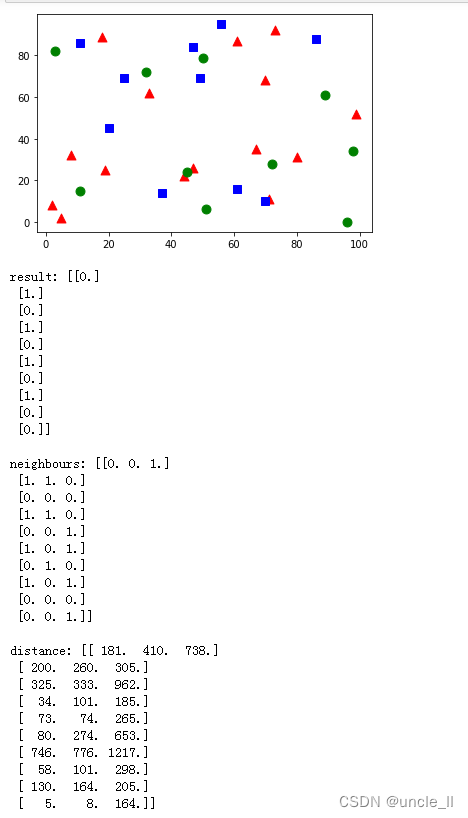
下面看看它是如何工作的，新样本被标记为绿色。

# Feature set containing (x,y) values of 25 known/training data
trainData = np.random.randint(0, 100, (25, 2)).astype(np.float32)

# Label each one either Red or Blue with numbers 0 and 1
responses = np.random.randint(0, 2, (25, 1)).astype(np.float32)


# Take Red neighbours and plot them
red = trainData[responses.ravel()==0]
plt.scatter(red[:, 0], red[:, 1], 80, 'r', '^')

# Take Blue neighbours and plot them
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:, 0], blue[:, 1], 80, 'b', 's')

newcomer = np.random.randint(0, 100, (1, 2)).astype(np.float32)
plt.scatter(newcomer[:, 0], newcomer[:, 1], 80, 'g', 'o')

knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, responses)

ret, results, neighbours, dist = knn.findNearest(newcomer, 3)

print("result: {}\n".format(results))
print("neighbours: {}\n".format(neighbours))
print("distance: {}\n".format(dist))

plt.show()

得到了如下的结果：

它说我们的新样本有3个近邻，一个来自Red家族，另外两个来自Blue家族。因此，他被标记为蓝色家庭。

如果有大量数据，则可以将其作为数组传递。获得的相应的结果是以数组的形式出现。

# Feature set containing (x,y) values of 25 known/training data
trainData = np.random.randint(0, 100, (25, 2)).astype(np.float32)

# Label each one either Red or Blue with numbers 0 and 1
responses = np.random.randint(0, 2, (25, 1)).astype(np.float32)


# Take Red neighbours and plot them
red = trainData[responses.ravel()==0]
plt.scatter(red[:, 0], red[:, 1], 80, 'r', '^')

# Take Blue neighbours and plot them
blue = trainData[responses.ravel()==1]
plt.scatter(blue[:, 0], blue[:, 1], 80, 'b', 's')

# newcomer = np.random.randint(0, 100, (1, 2)).astype(np.float32)
newcomers = np.random.randint(0,100,(10,2)).astype(np.float32)  # 10 new-comers
plt.scatter(newcomers[:, 0], newcomers[:, 1], 80, 'g', 'o')

knn = cv2.ml.KNearest_create()
knn.train(trainData, cv2.ml.ROW_SAMPLE, responses)

ret, results, neighbours, dist = knn.findNearest(newcomers, 3)  # The results also will contain 10 labels.
plt.show()
print("result: {}\n".format(results))
print("neighbours: {}\n".format(neighbours))
print("distance: {}\n".format(dist))

附加资源

• NPTEL notes on Pattern Recognition, Chapter 11
• Wikipedia article on Nearest neighbor search
• Wikipedia article on k-d tree