用python计算变量间相关性

本文从连续性数据和分类数据来分别展开计算变量间的相关性系数，其中分类变量的相关性系数计算较为复杂，运用了两种方法：（1）根据熵来算相关系数；（2）根据Gini系数计算相关系数
其中连续性数据相关性分析的数据源来自：百度网盘，相应的课程来源：慕课网

数据源

共包括10个变量，如下：satisfaction_level（满意度）,last_evaluation（上司评价）,number_project（项目数量）,average_monthly_hours（每月工作市场）,time_spend_company（在公司的时间）,Work_accident（工作事故）,left（离职率）,promotion_last_5years（五年内是否晋升）,department（部门）,salary（工资高低）。

一.连续性数据

连续性数据可用相关系数直接衡量。

import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns
#导入相应的模块
sns.set_context(font_scale=1.5)
#设置字体大小为1.5倍
df=pd.read_csv(r'C:\Users\me\Desktop\HR.csv')
#读入数据
df=df.dropna(how='any',axis=0)
#删除缺失值
df=df[df['last_evaluation']<=1][df['salary']!='nme'][df['department']!='sale']
#删除异常值
sns.heatmap(df.corr(),vmin=-1,vmax=1,cmap=sns.color_palette('RdBu',n_colors=128))
#画热力图，图例最小值 -1，最大值1，颜色对象设为红蓝('RdBu'),颜色数目为128
plt.show()

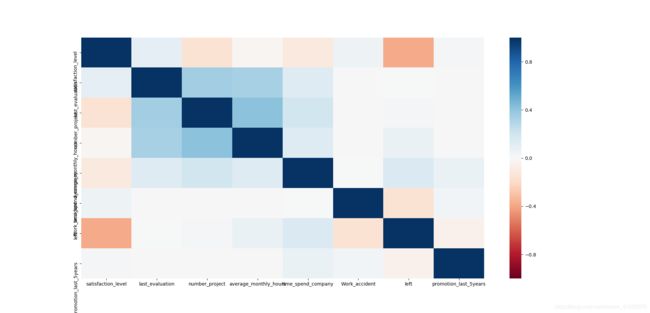蓝色代表接近1（正相关），红色代表接近于-1（负相关），颜色越深，相关性越强。

二.离散型数据

两类离散属性数据的相关性，只有两个分类，可编码为1或0，可用皮尔逊系数或Gini系数来计算。
多类离散属性数据如果为定序数据，可编码成0，1，2，3…，然后计算皮尔逊相关系数，但结果会存在失真。
更普遍的是，使用熵这个定义计算离散数据的相关性。

1.根据熵来算相关系数

名词解读

（1）熵（信息熵）

熵定义为：信息的数学期望。
熵越大，就越无序，越混乱。概率确定事件熵最小 = 0，随机事件 X 可以取的值越多，对应的熵值越大，也就是通常说的越“混乱”。
样本都属于一个类别，熵为0，样本的类别越多，分别越均匀，信息熵越大。

举例

已知事件X 的概率分布：p(x0)=1，p(x1)=0

x0	x1
1	0

计算 X 的熵。
根据公式，熵 H 是信息的期望，先求信息：
l(x0) = -log2(p(x0)) = -log2(1) = 0
l(x1) = -log2(0) = -Infinity
所以 H = l(x0) * p(x0) + l(x1) * p(x1) = 0 * 1 - 0 * Infinity = 0

结果与确定事件熵为 0 相吻合。

---

已知事件 X 的概率分布：p(x0)=0.5，p(x1)=0.5，计算 X 的熵。
l(x0) = l(x1) = -log2(0.5) = 1
H = 0.5 * 1 + 0.5 * 1 = 1

可见不确定事件比确定事件熵要大，即数据更混乱。

---

已知事件 X 的概率分布：x0=1/3 x2=1/3 x3=1/3，计算 X 的熵。

首先直觉上猜测一下这次 X 取三个值，比上一次更混乱，熵应该更大才对。
l(x0) = l(x1) = l(x2) = -log2(1/3) = 1.585
H = 3 * 1.585 * 1/3 = 1.585

可见：
确定事件熵最小 = 0；
随机事件 X 可以取的值越多，对应的熵值越大，也就是通常说的越“混乱”。

---

(2)条件熵

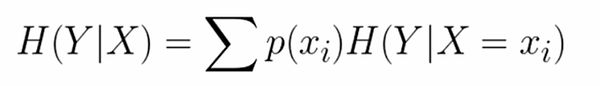
X条件下Y的条件熵表示在X条件下，Y 的不确定性程度。条件熵相对于原来的熵，会有所下降。

(3)互信息（熵增益）

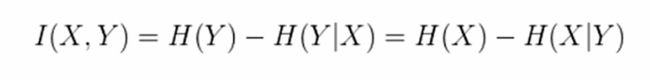
互信息的含义是这个过程中减少的熵，X与Y的互信息和Y与X的互信息是一致的。互信息也可叫做信息增益，缺点是对分类比较多的数据，有不正确的偏向，不具有归一化的特点，不确定性上不封顶，对于分类和相关性的界定不太方便。

(4)熵增益率

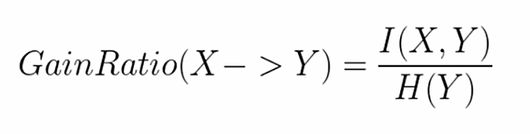
熵的增益率为熵的互信息除以Y的熵，由于熵的互信息小于Y的熵，所以这个值小于1，又由于熵的值大于0，所以该值大于0，所以能得到一个0~1的值。但由于熵的增益率不对称 ，也就是说X对Y的熵的增益率与Y对X的熵的增益率是不一致的，所以也不能用来进行衡量两者之间的相关性，需要对其进行转化，转化为以下形式。

（5）相关性

2.实例分析

（1）计算熵

s1=pd.Series(['X1','X1','X2','X2','X2','X2'])
s2=pd.Series(['Y1','Y1','Y1','Y2','Y2','Y2'])
#建立两个数组
def getEntropy(s): #定义熵
    if not isinstance(s,pd.core.series.Series):
        s=pd.Series(s) #把不是数组的数据转化为数组
    prt_ary=pd.groupby(s,by=s).count().values/float(len(s)) #得到概率分布
    return -(np.log2(prt_ary)*prt_ary),sum() #求和，得出熵
print('Entropy:',getEntropy(s1)) #输出s1的熵

结果为：

（2）计算条件熵

def getCondEntropy(s1,s2): #定义s1的条件s2的熵
    d=dict() #定义一个字典结构体
    for i in list(range(len(s1))):
        d[s1[i]]=d.get(s1[i],[])+[s2[i]] #key是s1的值，value是一个数组，为s2的值，记录了s1的值下s2的分布
    return sum([getEntropy(d[k])*len(d[k]/float(len(s1)) for k in d)])
print('CondEntropy',getCondEntropy(s1,s2)) #输出条件熵

输出结果为：

（3）计算熵增益

def getEntropyGain(s1,s2):
    return getEntropy(s2)-getCondEntropy(s1,s2) #s2的熵减s2条件下s1的熵
print('EntropyGain',getEntropyGain(s1,s2)) 

输出结果：

（4）熵增益率

def getEntropyGainRatio(s1,s2):
    return  getEntropyGainRatio(s1,s2)/getEntropy(s2) #熵增益除以熵
print('EntropyGainRatio',getEntropyGainRatio(s1,s2))

输出结果：

（5）相关性

import math  引入math包，求开方需要用到
def getDiscreteCorr(s1,s2):
    return getEntropyGain(s1,s2)/math.sqrt(getEntropy(s1)*getEntropy(s2))
print('DiscreteCorr',getDiscreteCorr(s1,s2))

输出结果：

这样，就得出了离散值之间的相关性度量了。

2.根据Gini系数计算相关系数

基尼系数和熵都有着类似的特质，它们都可以用来衡量信息的不确定性。
基尼系数的特质是：
（1）类别个数越少，基尼系数越低;
（2）类别个数相同时，类别集中度越高，基尼系数越低。
（3）当类别越少，类别集中度越高的时候，基尼系数越低；当类别越多，类别集中度越低的时候，基尼系数越高。
【类别集中度是指类别的概率差距，0.9+0.1的概率组合，比起0.5+0.5的概率组合集中度更高】
Gini系数计算公式如下：

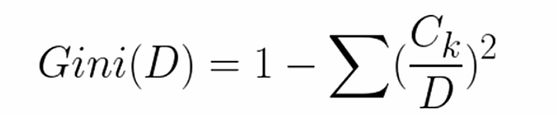
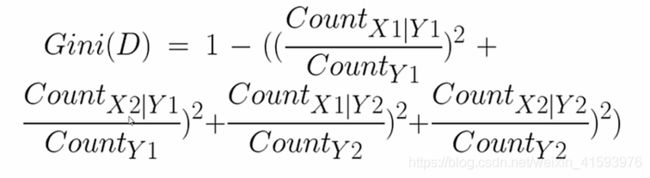
def getProbSS(s): #定义求概率平方和的函数
    if not isinstance(s, pd.core.series.Series):
        s = pd.Series(s)
    prt_ary = pd.groupby(s, by=s).count().values / float(len(s)) #取它的分布
    return sum(prt_ary**2) #取它的平方和
    
def getGini(s1,s2):  #与条件熵的算法类似
    d=dict()
    for i in list(range(len(s1))):
        d[s1[i]]=d.get(s1[i],[])+[s2[i]]
    return  1-sum([getProbSS(d[k])*len(d[k])/float(len(s1))  for k in d])
print('Gini',getGini(s1,s2))

输出结果为：