基于深度模型Out of Distribution(OOD)基础技术路线研究
在工业检测领域,将训练好的模型部署到实际场景时,常会碰到一个问题:如果输入的图片是一个新的类别,模型之前根本没见过,那么,无论模型的预测结果是什么,都必会是错误的。这种情况下,有两种选择:一种是将新出现的类别加入训练集,从新训练一个模型;另一种便是我们将要介绍的OOD检测方法。
问题定义和使用场景
定义:在分类任务中,给定测试图片![]() ,若模型在训练阶段模型见过或类似的图片,则能正确分类;但如果与训练集完全不相关,也会被强制判定为训练集类别中的一种,这种情况是不合理的。OOD算法希望能判断的分布状况是否与训练集一致,若一致,则称为in-distribution(ID),否则称为out-of-distribution(OOD)。
,若模型在训练阶段模型见过或类似的图片,则能正确分类;但如果与训练集完全不相关,也会被强制判定为训练集类别中的一种,这种情况是不合理的。OOD算法希望能判断的分布状况是否与训练集一致,若一致,则称为in-distribution(ID),否则称为out-of-distribution(OOD)。
使用场景举例:在MNIST上训练的一个分类模型,然后,输入一张“马”的图片,会被归类为数字0~9,这是错误的。此时,MNIST数据集就是in-distribution,相对于ID而言,“马”是out-of-distribution。
本文将为大家介绍五种OOD检测方法
1- 基于softmax的OOD检测方法
在分类网络中,对![]() 进行
进行![]() 运算,可以得到概率向量。而基于
运算,可以得到概率向量。而基于![]() 的OOD检测方法,就是利用了概率向量的特点,直接判定
的OOD检测方法,就是利用了概率向量的特点,直接判定![]() 是ID样本还是OOD样本。本节介绍MSP和ODIN,两者都是OOD领域较为经典的方法。
是ID样本还是OOD样本。本节介绍MSP和ODIN,两者都是OOD领域较为经典的方法。
1- 1 - MSP
MSP是Maximum Softmax Probability的缩写。在分类任务中,分类器的输出概率为![]() ,其中,
,其中,![]() 是预先设定的类别总数。给定
是预先设定的类别总数。给定![]() ,若标签
,若标签![]() ,则
,则![]() 很大,其余分量很小;而且,实验发现,若
很大,其余分量很小;而且,实验发现,若![]() 为OOD样本,那么
为OOD样本,那么![]() 的任意分量都很小,说明模型不确定
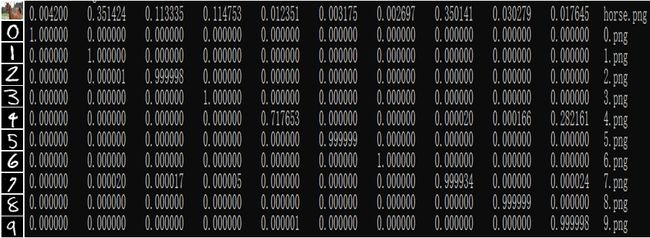
的任意分量都很小,说明模型不确定![]() 的类别。如下图所示,使用MNIST数据集训练的模型进行推理,会发现“马”的概率向量的每个分量都很小,而在数字0~9的概率向量中,都有一个特别大的分量。
的类别。如下图所示,使用MNIST数据集训练的模型进行推理,会发现“马”的概率向量的每个分量都很小,而在数字0~9的概率向量中,都有一个特别大的分量。
正是利用了这个特性,MSP定义OOD分数定义为
![]()
如果分数较大,判定![]() 为ID样本,否则判为OOD样本。
为ID样本,否则判为OOD样本。
MSP的缺点:当ID与OOD区别较大时,效果好;区别较小时,效果较差。在NuSA的介绍中,会看到这是因为从特征到logits会丢失了OOD样本的一些信息。
1 - 2 - ODIN
ODIN代表着Out-of-DIstribution detector for Neural networks,它在MSP的基础上,引入了temperature scaling和input preprocessing,使ID样本和OOD样本之间的区分度变大。
首先,介绍temperature scaling。在MSP中,OOD分数为
而在ODIN中,引入了一个温度因子![]() ,变成了
,变成了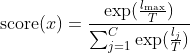 ,通过Taylor展开,可以分析这样做的好处。利用
,通过Taylor展开,可以分析这样做的好处。利用![]() ,可以得到
,可以得到
最终,![]() 。若
。若![]() 是ID样本,我们希望
是ID样本,我们希望![]() 很大。事实上,
很大。事实上,![]() 会比较大,但
会比较大,但 ![]() 也很大,导致
也很大,导致 ![]() 被
被 ![]() 削弱,此时只需增大
削弱,此时只需增大 ![]() 即可降低
即可降低 ![]() 的影响。若
的影响。若 ![]() 是OOD样本,我们希望
是OOD样本,我们希望 ![]() 比较小。事实上,
比较小。事实上,![]() 确实会比较小,
确实会比较小,![]() 也很小,导致
也很小,导致 ![]() 很小,结果增大
很小,结果增大 ![]() 不影响OOD样本。总结起来,增大
不影响OOD样本。总结起来,增大 ![]() 对OOD样本影响不大,但能使ID样本分数更高,增大了分离性。
对OOD样本影响不大,但能使ID样本分数更高,增大了分离性。
其次是input preprocessing,就是对输入进行预处理,使ID样本和OOD样本的分离性变大。从梯度下降法的角度进行分析,以 ![]() 为目标函数,
为目标函数,![]() 为变量。若沿着负梯度方向
为变量。若沿着负梯度方向 ![]() 更新
更新 ![]() ,可使
,可使 ![]() 变小。对于ID样本,我们希望
变小。对于ID样本,我们希望 ![]() 变大,所以要沿着正梯度方向
变大,所以要沿着正梯度方向 ![]() 更新
更新 ![]() ,即
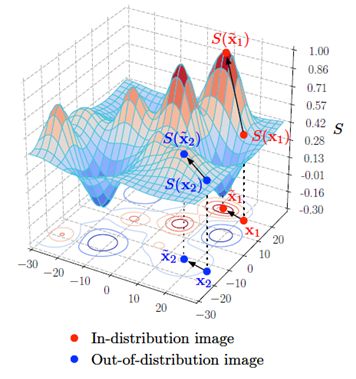
,即 ![]() 。实验发现, in-distribution图片置信度受到增强,out-of-distribution图片置信度也增强,只不过前者增幅更大,从而使ID与OOD之间的分离性得到提升,如下图所示。
。实验发现, in-distribution图片置信度受到增强,out-of-distribution图片置信度也增强,只不过前者增幅更大,从而使ID与OOD之间的分离性得到提升,如下图所示。
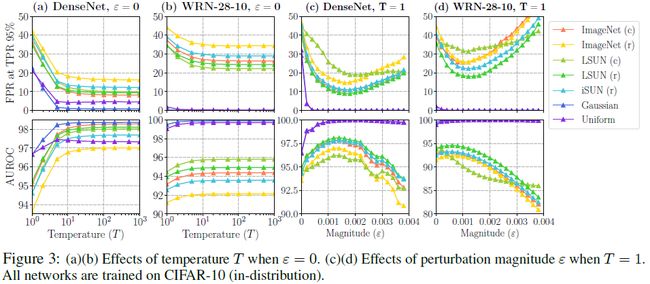
最终,通过实验,验证temperature scaling和input preprocessing的效果,如下图所示。
ODIN的缺点:尽管ODIN在MSP的基础上有了一定的改善,但是,它还是在MSP的整体框架之中,难有大的提升。
2- 基于feature的OOD检测方法
MSP和ODIN都是基于softmax的概率向量直接定义OOD分数,而Mahalanobis和NuSA则提供了一种新的思路,利用特征构造OOD分数。
2 - 1 - Mahalanobis
利用Mahalanobis距离函数,定义OOD分数为
![]() 。可以理解为,对于in-distribution中的每一个类别,都找一个中心,总共有
。可以理解为,对于in-distribution中的每一个类别,都找一个中心,总共有![]() 个中心
个中心 ![]() ;给定待测样本
;给定待测样本 ![]() ,如果它到任意一个中心都很远,那么是OOD样本。
,如果它到任意一个中心都很远,那么是OOD样本。
Mahalanobis的缺点:Mahalanobis保留了OOD样本的关键信息,但分类器训练好了却没有利用,导致分类结果的信息完全没有被用来进行OOD判断,而MSP实验显示,这些信息有助于提升ID样本的检测效果。
2- 2 - NuSA
给定一张图片 ![]() ,通过网络得到特征
,通过网络得到特征 ![]() ,再由线性变换得到 logits ,即
,再由线性变换得到 logits ,即 ![\text{logits}=l=W^T x=\left[\begin{matrix}w_1^Tx\\w_2^Tx\\\vdots\\w_C^Tx\end{matrix}\right]](http://img.e-com-net.com/image/info8/8bafee29f59e4ec3a4711f15dcda79a5.gif)
可以看到,特征 ![]() 与
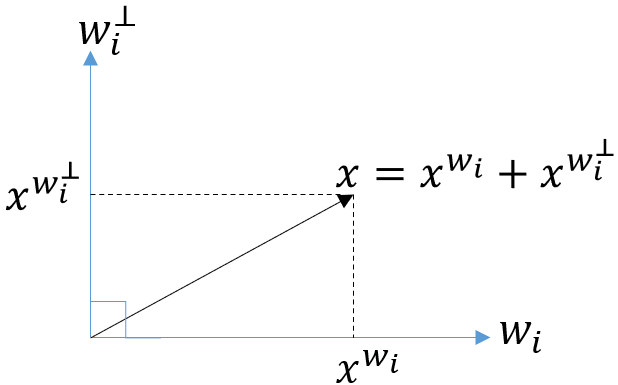
与 ![]() 之间,只差了一个线性变换。将
之间,只差了一个线性变换。将 ![]() 投射至
投射至 ![]() 方向,如下图所示,
方向,如下图所示,
得到 ![]() ,由于
,由于 ![]() ,所以
,所以 ![]() 是否属于第
是否属于第 ![]() 类,完全由
类,完全由 ![]() 决定,而与
决定,而与 ![]() 无关。此时,称
无关。此时,称 ![]() 是第
是第 ![]() 类的类别向量。更一般地,将
类的类别向量。更一般地,将 ![]() 投射至空间
投射至空间 ![]() ,则
,则 ![]() 。可以看到,在分类任务中,从特征
。可以看到,在分类任务中,从特征 ![]() 到
到 ![]() 的过程,
的过程, ![]() 携带的信息被“扔掉了”,导致
携带的信息被“扔掉了”,导致 ![]() 被强制预测为
被强制预测为 ![]() 中的某一类。
中的某一类。
如果 ![]() 是In Distribution,那么,从特征
是In Distribution,那么,从特征 ![]() 至 logits 的过程,其信息将被大量保存至
至 logits 的过程,其信息将被大量保存至 ![]() ,损失的信息量
,损失的信息量 ![]() 很小;如果
很小;如果 ![]() 是Out-Of-Distribution,那么,
是Out-Of-Distribution,那么, ![]() 不应该被分类为
不应该被分类为 ![]() 中任何一类,
中任何一类, ![]() 就会很大。
就会很大。
NuSA具有与Mahalanobis方法一样的缺点:NuSA保留了OOD样本的关键信息,但分类器训练好了却没有利用,导致分类结果的信息完全没有被用来进行OOD判断,而MSP已证明,这些信息有助于提升ID样本的检测效果。
3- softmax和feature相结合的OOD检测方法
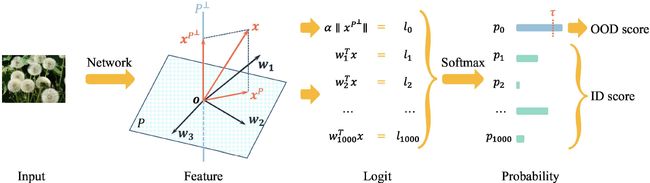
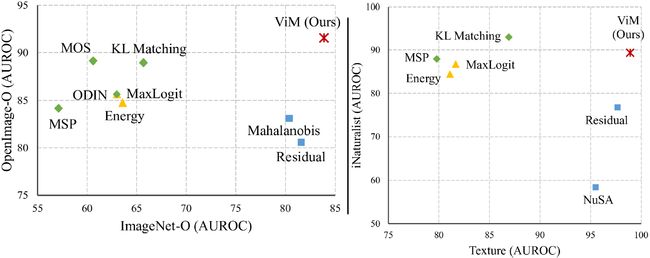
本节介绍一种将softmax和feature相结合的OOD检测方法,ViM(Out-Of-Distribution with Virtual-logit Matching)。ViM的作者使用ImageNet-1K作为ID样本,又分别使用OpenImage-O、ImageNet-O、Texture和iNaturalist作为OOD样本,检验每种方法的效果。如下图,基于softmax的方法时好时坏,基于feature的方法也一样有波动。
更重要的是,基于softmax的方法较差时,基于feature的方法往往有较好的效果,反过来也有一样的规律。softmax和feature之间形成了一定的优势互补,于是,ViM要将两者进行统一。
3 - 1 - ViM的原理
假设训练集有 ![]() 张图片,经网络提取获得
张图片,经网络提取获得 ![]() 个特征,记为
个特征,记为 ![]()
![]() 的维度为
的维度为 ![]()
的 ![]() 个最大的特征值对应的特征向量,得到
个最大的特征值对应的特征向量,得到 ![]() 维主空间(principal space)
维主空间(principal space) ![]()
![]() 是ID样本的主空间,将ID样本
是ID样本的主空间,将ID样本 ![]() 投射至
投射至 ![]() ,损失的信息
,损失的信息 ![]() 数值较小;将OOD样本
数值较小;将OOD样本 ![]() 投射至
投射至 ![]() ,损失的信息较多,此时
,损失的信息较多,此时 ![]() 数值较大。主空间
数值较大。主空间 ![]() 的维数低,但特征更关键、更本质。
的维数低,但特征更关键、更本质。
除主空间外,剩余的特征向量记为 ![]() 那么,
那么, ![]() 。
。
最终, 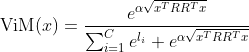 ,在原分类网络增加一个虚拟的logit分支(virtual logit),变成了
,在原分类网络增加一个虚拟的logit分支(virtual logit),变成了 ![]() 个类别的分类问题,如下图所示。
个类别的分类问题,如下图所示。
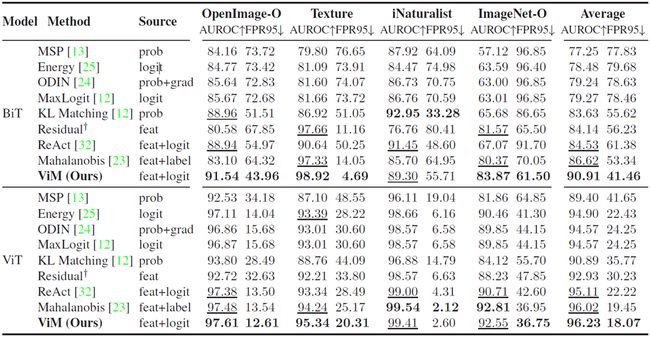
3- 2 - ViM的实验结果
实验设置为:
- ID样本:ImageNet-1K,包含1000个类别;
- OOD样本:OpenImage-O、Texture、iNaturalist、ImageNet-O,不是混杂在一起,而是逐一作为OOD数据集;
- 8种对比方法:MSP、Energy、ODIN、MaxLogit、KL Matching、Residual、ReAct、Mahalanobis,直接使用预训练模型,不再进行fine-tuning;
- 网络结构:第一种网络结构BiT、第二网络结构ViT;
- 评价指标:AUROC(越大越好)、FPR95 (FPR@TPR95,越小越好),只考虑ID与OOD之间的辨析,不考虑ID内部是否正确分类,因为不进行fine-tuning。
实验结果显示,ViM在4个OOD数据集上的指标都很好,同时具备了基于softmax和基于feature的方法的优点。
总结起来,模型在上线部署时,怎么处理从未见过的新类型数据,决定了系统是否稳定。而本文介绍的五种OOD检测方法,分别从不同的思路出发,为应对这种挑战提供了解决方案。随着未来更多新思路、新方法的涌现,OOD检测一定会变得更强大,帮助更多模型可靠地运行。
|参考文献
- MSP: Dan Hendrycks and Kevin Gimpel. A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks. ICLR 2017.
- ODIN: Shiyu Liang and Yixuan Li et al. Enhancing the reliability of out-of-distribution image detection in neural networks. ICLR 2018.
- Mahalanobis: Kimin Lee1 and Kibok Lee et al. A Simple Unified Framework for Detecting Out-of-Distribution Samples and Adversarial Attacks. NeurIPS 2018.
- NuSA: Matthew Cook and Alina Zare et al. Outlier detection through null space analysis of neural networks. arXiv 2020.
- ViM: Haoqi Wang and Zhizhong Li et al. ViM: Out-Of-Distribution with Virtual-logit Matching. CVPR 2022.

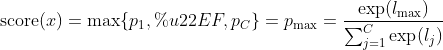
![U_1=\frac{1}{C-1}\sum_{i\neq i_{\text{max}}}^C [l_{\text{max}}-l_i], U_2=\frac{1}{C-1}\sum_{i\neq i_{\text{max}}}^C [l_{\text{max}}-l_i]^2.](http://img.e-com-net.com/image/info8/91a75354c99346c6ae163cfdcb79e50d.gif)

![X^TX=Q\Lambda Q^T=[e_1, \cdots , e_N]\left[\begin{matrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_N \end{matrix}\right]\left[\begin{matrix} e_1^T\\ \vdots\\ e_N^T \end{matrix}\right]](http://img.e-com-net.com/image/info8/a2ab85fe2bd9443292094b101fd3dcf7.gif)