通过R语言实现平稳时间序列的建模--基础(ARMA模型)
目录
1. 建模流程
2. 序列平稳性检验和纯随机性检验
2.1 图检验
2.2 单位根检验
3. 模型选择
4. 参数估计
5. 模型检验
5.1 模型显著性检验
5.2 参数显著性检验
6. 模型优化
6.1 AIC准则
6.2 BIC准则
7. 预测
1. 建模流程
1.1 序列平稳性检验+纯随机性检验
1.2 模型选择
1.3 参数估计
1.4 模型检验
1.5 模型优化
1.6 预测
2. 序列平稳性检验和纯随机性检验
2.1 图检验
主要适用于趋势或者周期比较明显的序列,具有一定主观性。
(1)绘制时序图与自相关图:
x<-read.csv("C:/Users/M/Desktop/4.9.csv") #读入csv数据
dwelling<-ts(x,start = c(1971,9),frequency = 12)#构造时间序列变量
#start:指定序列起始时间,如start=c(1990,2)即1990年2月;start=1990即1990年。
#frequency:指定学列每年读入的数据频率,如frequency=12即每年读入12个数据,月度数据;frequency=4即读入季度数据;诸如此类。
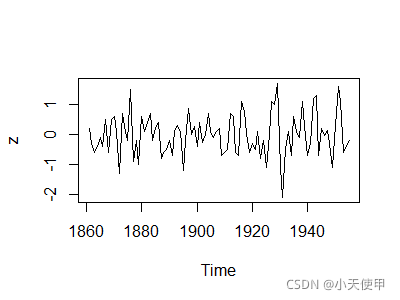
plot(dwelling) #输出时序图
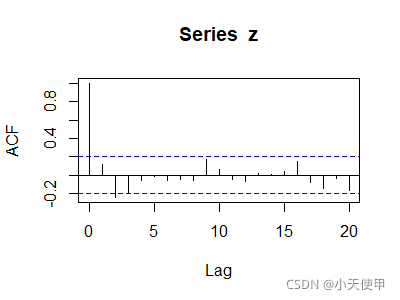
acf(dwelling,lag.max=12,plot=T)
#acf(变量名,延迟阶数,选择输出自相关图或者自相关系数)
#lag.max:若缺省该参数,系统会根据序列长度自动指定延迟阶数。
#plot:系统默认参数为plot = Ture,即只输出自相关图不输出自相关系数;plot=False,只输出自相关系数。
acf(time)$acf #查看具体的自相关系数从时序图可见该序列没有明显的趋势和周期,从自相关图可见该序列除了延迟1~4阶外,其他自相关系数均在两倍标准差内,可以认为该序列具有短期相关性。因此判断该序列为平稳序列。
(2)纯随机检验
纯随机序列序列没有建模的必要,因为序列值之间无相关性,历史数据对未来数据无影响。
用Box.test 函数进行纯随机性检验:
Box.test(dwelling,lag=6,type="Ljung-Box") #延迟6阶
Box.test(dwelling,lag=12,type="Ljung-Box") #延迟12阶
#lag: 缺省该参数时,默认输出之后1阶的检验统计量结果
#type:选择检验统计量的类型,默认为type="Box-Pierce",输出白噪声检验的Q统计量;type="Ljung-Box"输出LB统计量
#输出情况如下
> Box.test(dwelling,lag=6,type="Ljung-Box") #延迟6阶
Box-Ljung test
data: dwelling
X-squared = 215.96, df = 6, p-value < 2.2e-16
> Box.test(dwelling,lag=12,type="Ljung-Box") #延迟12阶
Box-Ljung test
data: dwelling
X-squared = 329.2, df = 12, p-value < 2.2e-16白噪声检验显示延迟为6、12阶时p值均远远小于显著性水平0.05,因此显著拒绝序列为纯随机系列的原假设。因此判断该序列为非纯随机序列。
2.2 单位根检验
2.2.1 DF检验
仅适用于最简单的1阶模型AR(1)的平稳性检验。
调用aTSA中的的adf.test 函数进行DF检验:
install.packages("aTSA")
library(aTSA)
adf.test(dwelling,nlag=2)
#nlag:最高延迟阶数,若nlag=1即输出自回归0阶延迟平稳性检验结果;若nlag=2即输出自回归0至1阶延迟平稳性检验结果。
#输出结果
> adf.test(dwelling,nlag=2)
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -2.46 0.0162
[2,] 1 -1.90 0.0573
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -4.81 0.01
[2,] 1 -3.68 0.01
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -4.97 0.0100
[2,] 1 -3.89 0.0185
----
Note: in fact, p.value = 0.01 means p.value <= 0.01 如上检验结果,类型一二三的p值(p.value)均小于显著性水平0.05,因此可以判断该序列显著平稳。
只要有一个类型的p值能够通过显著性检验,即可判断序列平稳。
2.2.2 ADF检验
DF检验修正后增广DF检验,即ADF检验,适用于任意p阶模型的平稳性检验。
adf.test(dwelling)
#输出结果
> adf.test(dwelling)
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -2.46 0.0162
[2,] 1 -1.90 0.0573
[3,] 2 -1.38 0.1832
[4,] 3 -1.10 0.2827
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -4.81 0.010
[2,] 1 -3.68 0.010
[3,] 2 -2.43 0.161
[4,] 3 -1.94 0.350
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -4.97 0.0100
[2,] 1 -3.89 0.0185
[3,] 2 -2.60 0.3254
[4,] 3 -2.03 0.5579
----
Note: in fact, p.value = 0.01 means p.value <= 0.01 3. 模型选择
在一个序列被确定为平稳白噪声序列后,我们可以根据样本自相关性系数与偏自相关性系数的性质选择合适的ARMA模型拟合序列。
| 自相关系数 | 偏自相关系数 | 模型定阶 |
| 拖尾 | p阶截尾 | AR(p)模型 |
| q阶截尾 | 拖尾 | MA(p)模型 |
| 拖尾 | 拖尾 | ARMA(p,q)模型 |
截尾:若样本(偏)自相关系数最初R阶明显超出2倍标准差范围,但此后95%的(偏)自相关系数均在2倍标准差内,且数值衰减成小值波动的过程非常突然。
拖尾:若有超过5%的样本(偏)自相关系数落在2倍标准差外,或者,由显著非零的(偏)自相关系数衰减为小值波动的过程较为缓慢或连续。
绘制自相关系数图与偏自相关系数图:
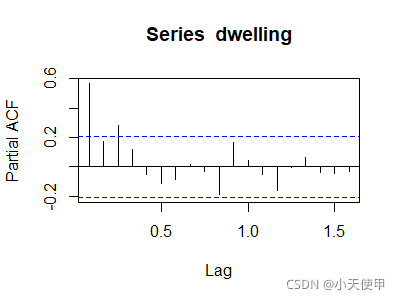
acf(dwelling) #自相关系数图
pacf(dwelling) #偏自相关系数图自相关系数图显示出较为缓慢且连续地衰减,这是自相关系数拖尾的表现。偏自相关系数图显示除了延迟2阶偏自相关系数在2倍标准差范围内,其他均在2倍标准差范围内波动,这是偏自相关系数截尾的特征。因此可以将该序列模型定阶为AR(1)。
4. 参数估计
通过 arima 函数进行参数估计:
arima(dwelling,order=c(1,0,0))
#order=c(p,d,q):p为自回归阶数;d为差分阶数,不涉及差分时可以取0;q为移动平均阶数。
#method:指定参数估计方法,默认为method="CSS-ML" 即条件最小二乘与极大似然估计混合方法;method="CSS" 即条件最小二乘估计方法;method="ML" 即极大似然估计方法。
#输出结果:
> arima(dwelling,order=c(1,0,0),method="ML")
Call:
arima(x = dwelling, order = c(1, 0, 0), method = "ML")
Coefficients:
ar1 intercept
0.5929 40.5062
s.e. 0.0877 4.6893
sigma^2 estimated as 331.3: log likelihood = -380.41, aic = 766.82第一行输出的是参数估计值,第二行输出的是参数估计值的样本标准差。
或者,通过输出的参数得到![]() ,
, ![]() ,
,
因此得到AR(1)模型为:![]() 。
。
5. 模型检验
5.1 模型显著性检验
如果残差序列为非白噪声检验,则意味着残差序列中依旧含有未被模型提取的相关信息,这就说明这个拟合模型不够有效。因此,模型的显著性检验即残差序列的白噪声检验。
原假设为该序列的残差均为0。
fit=arima(dwelling,order=c(1,0,0),method="ML") #fit为arima函数拟合结果
ts.diag(fit) #进行模型显著性检验,输出四个图
#左上的图为残差序列自相关图;右上的图为残差序列偏相关图
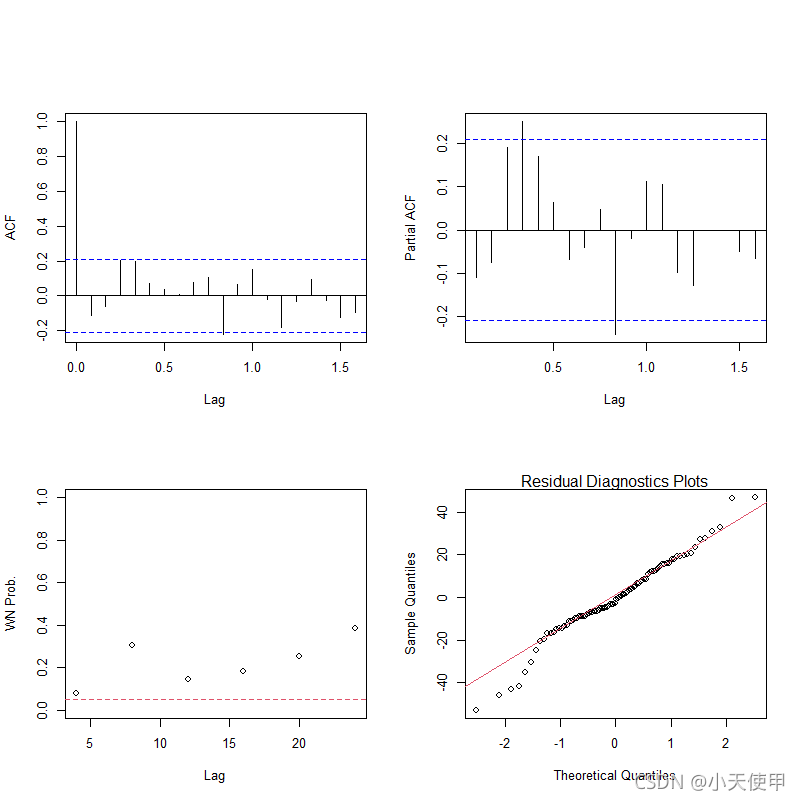
#左下的图为残差序列白噪声检验图;右下为残差序列正态性检验QQ图输出四图如下:
左下方的残差序列自相关图横轴为延迟阶数,纵轴为该延阶数纯随机性检验(Q统计量)的p值。若所有的点都在虚线上方,即所有Q统计量的p值均大于显著性水平0.05,此时可认为该模型显著成立。
右下方的残差序列正态性检验QQ图横轴为正态分布的分位数,纵轴为样本分位数,若图上的点密集分布在对称线左右,则可以认为该序列服从正态分布。该图可用以对序列进行正态分布假定的检验。
如图,由于残差序列自相关图上所有点均在虚线上方,即所有p值均显著大于0.05,可以认为该模型的残差序列为白噪声序列,即该模型通过了显著性检验。
5.2 参数显著性检验
即检验未知参数是否显著非零。若某个参数不显著非零,则可以从拟合模型中剔除,使得模型精简。
5.2.1 法一
当样本较大时,序列近似于正态分布,因此只要参数估计值大于其两倍标准差,我们就可以认为该参数显著非零。
此时只需要再使用一次arima函数:
arima(dwelling,order=c(1,0,0),method="ML")
#输出结果
> arima(dwelling,order=c(1,0,0),method="ML")
Call:
arima(x = dwelling, order = c(1, 0, 0), method = "ML")
Coefficients:
ar1 intercept
0.5929 40.5062
s.e. 0.0877 4.6893因为0.5929>0.0877*2,20.5062>4.6893*2,因此两个参数均显著非零。
5.2.2 法二
先构造参数显著性检验的t统计量,再通过pt函数求得p值:
t=abs(fit$coef)/sqrt(diag(fit$var.coef)) #构造t统计量
pt(t,length(dwelling)-length(fit$coef),lower.tail = F) #输出p值
#输出结果
> t=abs(fit$coef)/sqrt(diag(fit$var.coef))
> pt(t,length(dwelling)-length(fit$coef),lower.tail = F)
ar1 intercept
7.828497e-10 1.343084e-13 两个参数t统计量的p值均远小于显著性水平0.05,因此两个参数均显著非零。
6. 模型优化
一个好的模型是拟合精度与未知参数个数的综合最优配置,我们可以通过最小信息量检查AIC以及它的改进BIC准则来选出相对的最优模型。
6.1 AIC准则
AIC(fit)
#输出结果
AIC(fit)
[1] 766.8243可以对比多个模型的AIC值,使得AIC达到最小值的模型为相对最优模型。
6.2 BIC准则
BIC(fit)
#输出结果
> BIC(fit)
[1] 774.2563可以对比多个模型的BIC值,使得BIC达到最小值的模型为相对最优模型。
也可以同时考虑AIC函数值与BIC函数值,使得二者达到最小的模型为相对最优模型。
6.3 auto.arima 函数
该函数基于信息量最小原则,可以在一定范围内自动识别最优模型的阶数,可以起到简化模型优化问题的作用。
install.packages("forecast")
library("forecast")
auto.arima(dwelling,max.p=5,max.q=5,ic="bic")
#max.p:指定自相关系数的最高阶数,默认为5;
#max.q:指定移动平均系数的最高阶数,默认为5;
#ic:指定信息量准则,默认为ic="aic",即AIC准则;ic="bic"即BIC准则;此外还有ic="aicc"。
#输出结果
> auto.arima(dwelling,max.p=5,max.q=5,ic="bic")
Series: dwelling
ARIMA(1,0,1)(1,0,0)[12] with zero mean
Coefficients:
ar1 ma1 sar1
0.9648 -0.4870 0.3971
s.e. 0.0297 0.0951 0.1375
sigma^2 estimated as 296.6: log likelihood=-375.97
AIC=759.95 AICc=760.43 BIC=769.86考虑到输出的第二个参数值-0.4870<2*0.0951,即参数估计值小于2倍标准差,这个参数不显著非零,舍去,因此最优模型应该是AR(1) 。
7. 预测
可以通过forecast包中的forecast函数进行预测:
library("forecast")
fore=forecast(fit,h=10) #预测此后10期
#h:预测期数;
#level:置信区间的置信水平,默认为80%与95%的双层置信区间。
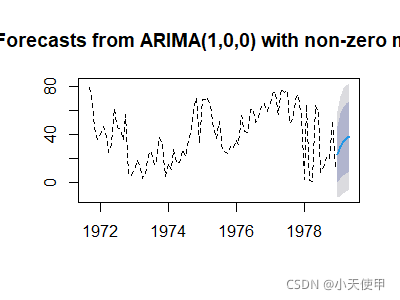
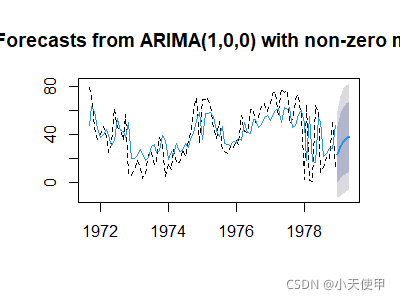
plot(fore,lty=2) #输出预测图
lines(fore$fitted,col=4) #在预测图上加上拟合值曲线
#图中虚线为观察值,实线为拟合值图中右边预测部分,深色区域为置信水平80%的预测值置信区间,浅色区域为置信水平为95%的预测置信区间。