公式写成matlab代码,大话遗传算法（含Matlab代码）

一、遗传算法简介

转载自：https://blog.csdn.net/acelit/article/details/78187715

在工程实践中，经常面临多变量、不可微、不连续、有约束等条件下的最优化问题，此时梯度下降法、牛顿法等传统的优化算法难以下手，智能算法却凭借不断迭代、概率变化逐步逼近全局最优解，从而达到“近似最优”的状态，所得结果往往能够满足实际工程应用精确度的要求。遗传算法(Genetic Algorithm, GA)是一类借鉴生物的自然选择和遗传进化机制而开发的一种全局最优算法，算法遵循“适者生存，优胜劣汰”的原则。通过模拟生物在自然选择中的进化过程，依靠选择(selection)、交叉(crossover)、变异(mutation)等机制对染色体(携带遗传信息)进行组合，实现染色体的不断更新，其中每条染色体对应问题的一个解，每次迭代筛选群体中满足适应度的后代，直至到达迭代次数或适应度值趋于稳定。

1、编码及群体初始化

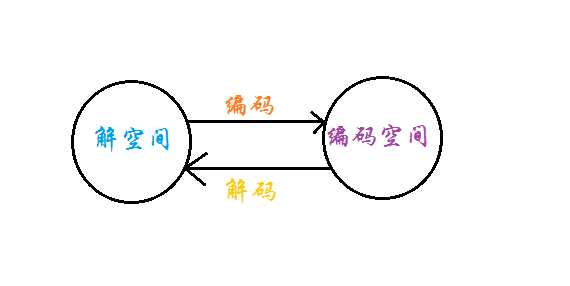
为方便染色体后续的迭代进化，首先需要对携带信息的染色体进行编码，目前有实数编码和二进制编码两种编码方式，各有优缺点。

实数编码：直接用实数表示基因，容易理解且不需要解码过程，但容易过早收敛，从而陷入局部最优

二进制编码：稳定性高，种群多样性大，但需要的存储空间大，需要解码且难以理解根据实际工程问题选择编码方式，在最后记得将优化结果解码为相应问题的实际解。

每条染色体对应解空间的一个解，称为“个体”，所有这些个体组成了一个种群。种群可按照随机生成的方式进行初始化。

其中，需要注意的有两个参数：

群体大小：染色体的条数即个体的数量，为进化提供选择、交叉操作。

染色体长度：实际解对应到编码空间解的长度，如果是二进制编码则是二进制的位数。

2、适应度函数

遗传算法在进化搜索中基本不利用外部信息，而是以适应度函数为依据，利用种群中每个个体的适应度值来进行优胜劣汰、进化种群，即适应度值大的个体以较大的概率遗传到下一代，而适应度值小的个体则以一定概率被淘汰，从而让种群往更优的方向进化。因此，适应度函数是种群评价的重要手段，其选取直接影响到遗传算法的收敛速度及最优解的质量。

最大迭代次数：通常会为算法设置最大迭代次数，一旦到达迭代次数程序终止，输出优化结果，提高算法效率。

3、遗传算子

由于种群刚开始是随机生成的，需要通过不断进化来提高解的质量。种群进化的能力包括三种：选择、交叉及变异，分别对应三种遗传算子。它们分别作用与群体X(k)，通过优胜劣汰、杂交以及变异，得到适应度更好的新一代群体X(k+1)。

(1)选择算子

将种群中的个体按照适应度的大小进行排列，按照某种选择方式对种群中的个体进行配对选择，作为下一代个体的父母。通常用“轮盘赌选择法”(Roulette Wheel Selection method)进行选择，各个个体被选中的概率与其适应度函数值大小成正比。

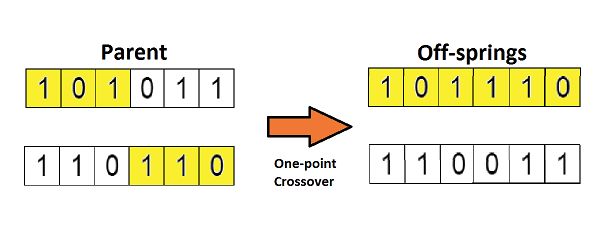
(2)交叉算子

将上一步选择的两个父母进行交叉繁殖，得到后代个体，交叉是通过交叉概率按照某种交叉方式交换部分基因。交叉方式包括单点交叉和多点交叉等。

交叉运算是遗传算法区别于其他进化算法的重要特征，它在遗传算法中起着关键作用，是产生新个体的主要方法。

(3)变异算子

最后按照变异概率采用某种变异形式对染色体进行变异，变异形式包括单点变异、多点变异等，将染色体编码串中的某些基因座上的基因值用该基因座的其他等位基因来替换，从而形成一个新的个体。

在遗传算法中，变异算子的作用主要是改善遗传算法的局部搜索能力，维持群体的多样性,防止出现早熟现象。

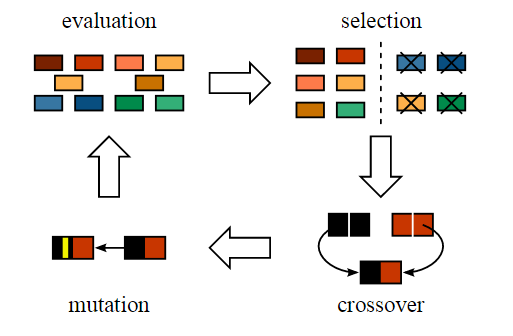
一般来说，交叉概率比较大，变异概率极低。经过选择-交叉-变异运算后，至此，我们得到了新的个体，完成了这轮的迭代，整体过程如下：

二、遗传算法流程

三、算例分析

问题：求解函数f(x)=x+10sin(5x)+7cos(4x)的最大值，x定义在[0,9]。

首先用matlab看一下该函数的形状：

设定目标函数的解精确到小数点后4位，则可以将x的解空间划分为(9-0)*10000=90000等分，而2^16<90000<2^17，可以选择二进制进行编码，编码位数(基因数)为17位。即每个个体(染色体，chromosome)都可以看成一个17位的二进制串。

设置：初始种群大小为100，交叉概率设置为0.6，变异概率设置为0.01，最大迭代次数为200。

population_size = 100; % 种群大小

chromosome_size = 17; % 染色体长度

generation_size = 200; % 最大迭代次数

cross_rate = 0.6; % 交叉概率

mutate_rate = 0.01; % 变异概率

解码：每一条染色体都可以通过解码的方式获得实际解，二进制解码公式为：

f(x), x∈[lower_bound, upper_bound]

x = lower_bound + decimal(chromosome)×(upper_bound-lower_bound)/(2^chromosome_size-1)

其中：

lower_bound:

函数定义域的下限upper_bound: 函数定义域的上限chromosome_size: 染色体的长度

对于本题：

x = 0 + decimal(chromosome)×(9-0)/(2^17-1)

初始化种群：种群个体population随机进行初始化。

for i=1:population_size

for j=1:chromosome_size

% 给population的i行j列赋值

population(i,j) = round(rand); % rand产生(0,1)之间的随机数，round()是四舍五入函数

end

end

计算个体适应度：本题的目标函数即可作为适应度函数，函数值越大表示该个体适应度越高。

upper_bound = 9; % 自变量的区间上限

lower_bound = 0; % 自变量的区间下限

% 所有种群个体适应度初始化为0

for i=1:population_size

fitness_value(i) = 0.;

end

% f(x) = x+10*sin(5*x)+7*cos(4*x);

for i=1:population_size

for j=1:chromosome_size

if population(i,j) == 1

fitness_value(i) = fitness_value(i)+2^(j-1); % population[i]染色体串和实际的自变量xi二进制串顺序是相反的

end

end

fitness_value(i) = lower_bound + fitness_value(i)*(upper_bound-lower_bound)/(2^chromosome_size-1); % 自变量xi二进制转十进制

fitness_value(i) = fitness_value(i) + 10*sin(5*fitness_value(i)) + 7*cos(4*fitness_value(i)); % 计算自变量xi的适应度函数值

end

选择：在选择之前先对个体的适应度进行排序，计算出每次迭代种群的平均适应度，再按照轮盘赌法选择进化的个体。

排序：

for i=1:population_size

fitness_sum(i) = 0.;

end

min_index = 1;

temp = 1;

temp_chromosome(chromosome_size)=0;

% 遍历种群

% 冒泡排序

% 最后population(i)的适应度随i递增而递增，population(1)最小，population(population_size)最大

for i=1:population_size

min_index = i;

for j = i+1:population_size

if fitness_value(j) < fitness_value(min_index);

min_index = j;

end

end

if min_index ~= i

% 交换 fitness_value(i) 和 fitness_value(min_index) 的值

temp = fitness_value(i);

fitness_value(i) = fitness_value(min_index);

fitness_value(min_index) = temp;

% 此时 fitness_value(i) 的适应度在[i,population_size]上最小

% 交换 population(i) 和 population(min_index) 的染色体串

for k = 1:chromosome_size

temp_chromosome(k) = population(i,k);

population(i,k) = population(min_index,k);

population(min_index,k) = temp_chromosome(k);

end

end

end

% fitness_sum(i) = 前i个个体的适应度之和

for i=1:population_size

if i==1

fitness_sum(i) = fitness_sum(i) + fitness_value(i);

else

fitness_sum(i) = fitness_sum(i-1) + fitness_value(i);

end

end

% fitness_average(G) = 第G次迭代 个体的平均适应度

fitness_average(G) = fitness_sum(population_size)/population_size;

% 更新最大适应度和对应的迭代次数，保存最佳个体(最佳个体的适应度最大)

if fitness_value(population_size) > best_fitness

best_fitness = fitness_value(population_size);

best_generation = G;

for j=1:chromosome_size

best_individual(j) = population(population_size,j);

end

end

选择：

for i=1:population_size

r = rand * fitness_sum(population_size); % 生成一个随机数，在[0,总适应度]之间

first = 1;

last = population_size;

mid = round((last+first)/2);

idx = -1;

% 排中法选择个体

while (first <= last) && (idx == -1)

if r > fitness_sum(mid)

first = mid;

elseif r < fitness_sum(mid)

last = mid;

else

idx = mid;

break;

end

mid = round((last+first)/2);

if (last - first) == 1

idx = last;

break;

end

end

% 产生新一代个体

for j=1:chromosome_size

population_new(i,j) = population(idx,j);

end

end

for i=1:population_size

for j=1:chromosome_size

population(i,j) = population_new(i,j);

end

end

交叉：

% 步长为2 遍历种群

for i=1:2:population_size

% rand

if(rand < cross_rate)

cross_position = round(rand * chromosome_size);

if (cross_position == 0 || cross_position == 1)

continue;

end

% 对 cross_position及之后的二进制串进行交换

for j=cross_position:chromosome_size

temp = population(i,j);

population(i,j) = population(i+1,j);

population(i+1,j) = temp;

end

end

end

变异：

for i=1:population_size

if rand < mutate_rate

mutate_position = round(rand*chromosome_size); % 变异位置

if mutate_position == 0

% 若变异位置为0，不变异

continue;

end

population(i,mutate_position) = 1 - population(i, mutate_position);

end

end

至此，遗传算法的个体进化步骤已经全部完成，接下来根据设置的最大迭代次数来终止程序的执行，获得最优个体，即最优二进制串，最后只要通过解码就可以得到问题的实际解。

matlab运行结果：

最优个体:

best_individual =

1 1 0 1 0 1 1 1 0 1 1 1 1 1 0 1 1

最优适应度:

best_fitness =

24.8553

最优个体对应自变量值:

x =

7.8560

达到最优结果的迭代次数:

iterations =

15

该问题的工程代码下载：链接：http://pan.baidu.com/s/1o8iK35C 密码：o661

四、Matlab遗传算法工具箱的使用

在较高版本的matalb(我用的是matlab2016b)中自带最优化工具箱，可以直接选择GA算法求解最优解。

1、编写目标函数

function [ y ] = target(x)

% 工具箱只支持求解最小值，将求解最大值变成求解最小值

y = -x-10*sin(5*x)-7*cos(4*x);

end

2、配置GUI界面

五、总结

以上是遗传算法的介绍和求解最优化问题的实例，下面简单总结一下遗传算法的优缺点如下：

优点：

1. 与问题领域无关切快速随机的搜索能力。

2. 搜索从群体出发，具有潜在的并行性，可以进行多个个体的同时比较。

3. 搜索使用评价函数(适应度函数)启发，过程简单。

4. 使用概率机制进行迭代，具有随机性。

5. 具有可扩展性，容易与其他算法结合。

缺点：

遗传算法的编程实现比较复杂，首先需要对问题进行编码，找到最优解之后还需要对问题进行解码。

三个算子的实现也有许多参数，如交叉概率和变异概率，并且这些参数的选择严重影响解的品质，而目前这些参数的选择大部分是依靠经验。

没有能够及时利用反馈信息，故算法的搜索速度比较慢，要得要较精确的解需要较多的训练时间。

算法对初始种群的选择有一定的依赖性，能够结合一些启发算法进行改进。

算法的并行机制的潜在能力没有得到充分的利用，这也是当前遗传算法的一个研究热点方向。

参考资料

[1] 陈智家. 燃料电池电动汽车动力系统参数匹配与优化研究[D]. 武汉理工大学, 2010.