机器学习—优化器与正则化
优化器
在介绍各类优化器之前,我们先来看一下经典的优化算法。
经典的优化算法可以分为直接法和迭代法两大类。
直接法就是直接对损失函数求导找出损失函数的全局最小值,但是这种方法具有两个局限性,首先损失函数必须是凸函数,其次损失函数倒数等于0的时候必须有闭式解,比如求解线性回归时,涉及到的矩阵的逆,可有些时候矩阵是不存在逆的,因此就无法求解,而且当数据维度较大时,矩阵的逆运算十分复杂会占用较大的内存,因此直接法通常不会被应用在实际应用中。
在深度学习中,迭代法往往被应用与对参数的更新。迭代法希望找到一个更好的估计值 θt+δ 来替代θ。迭代法分为一阶迭代和二阶迭代。一阶迭代被称为梯度下降法,而二阶迭代被称为牛顿法。
一阶迭代采用了对损失函数的一阶泰勒展开,即:
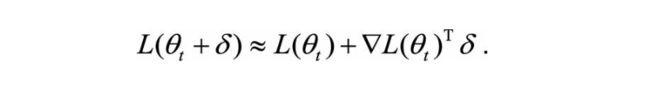
加上L2正则化,我们的目标变为:
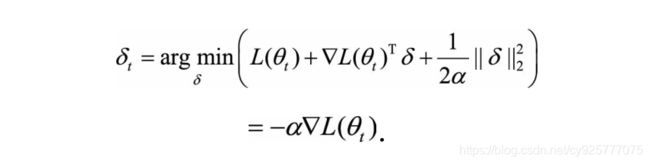
因此,一阶法的迭代公式为:
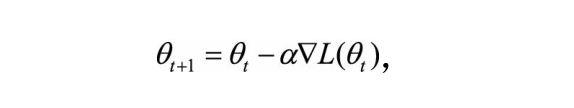
二阶法是对损失函数进行二阶泰勒展开:
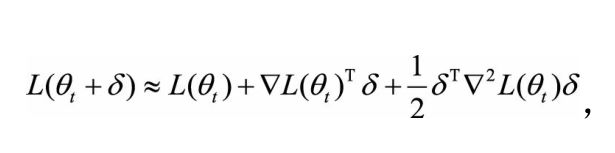

二阶法的迭代公式:
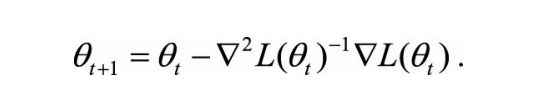
二阶法也称为牛顿法,Hessian矩阵就是目标函数的二阶信息。二阶法的收敛速度一般要远快于一阶法,但是在高维情况下,Hessian矩阵求逆的计算复杂度很大,而且当目标函数非凸时,二阶法有可能会收敛到鞍点(Saddle Point)。
好了,现在我们继续介绍优化器:
首先说一下梯度下降法的问题,梯度下降法在对参数进行更新时需要用到全部的数据,在深度学习中,数据量往往是是非庞大的,如果所有的数据都参数一次参数的更新,那计算开销和计算效率十分的低。因此,提出了随机梯度下降法(SGD)来解决这个问题。随机梯度下降只用到所有样本中的一个样本对参数进行更新,这大大的提高了反向传播的效率。但是,由于只用一个样本对参数进行更新会增加随机梯度的方差,因此大牛们又提出了小批量梯度下降(Mini-Batch Gradient Descent。该方法采用数据批处理的方式,每次更新只使用一小批数据进行更新,不仅降低了梯度的方差,还提高了反向传播的参数更新速度。
随机梯度下降
随机梯度下降在上面已经讲过了,因此这里只给出公式:
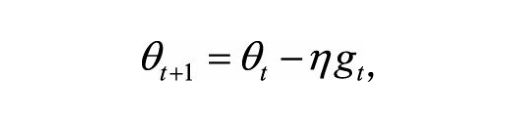
梯度每次更新取决于学习率和梯度,梯度控制下降的方向,学习力控下降的步伐,学习率越大,梯度下降得越快,但是学习率太大的话会使算法最后很难收敛,反之如果学习率太小的话会导致手链太慢的影响,因此学习率的调控对算法优化具有重大意义。
带有动量(Momentum)的梯度下降法
在梯度下降时,有两种情况最为致命,其一是“峡谷”,即局部极小值,梯度下降法会在峡谷内发生震荡。其二是鞍点,鞍点处的偏导数同样为零,会给算法造成已经收敛的假象。因此,我们希望算法在收敛时具有一定的“惯性”,这类似于运动物理学,如果算法下梯度下降时具有一定的惯性,那么可能会冲出峡谷和鞍点继续向全局最小值的方向收敛。
其实这个思想很简单,我们只需要在下一个更新的时刻添加上一时刻的方向,使其在原用的方向上保持一定的惯性,公式表达为:
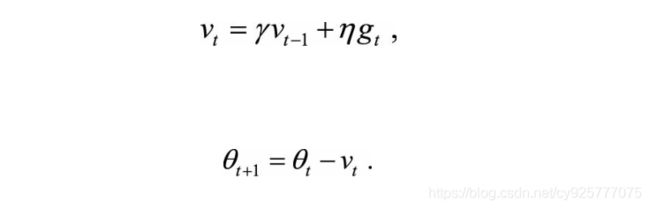
AdaGrad:
加入动量的梯度下降法虽然一定程度上克服了峡谷问题和鞍点问题,但是学习率需要人为不断调试。AdaGrad希望能够根据数据出现的频次以及时间的推移自适应的控制学习率,从而是优化过程更够更快更准的收敛,AdaGrad的公式如下:
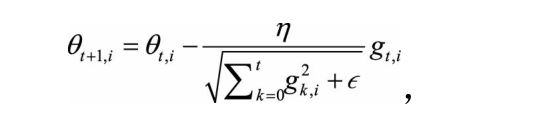
其中θ t+1,i 表示(t+1)时刻的参数向量θ t+1 的第i个参数,g k,i 表示k时刻的梯度向量g k的第i个维度(方向)。
通过公式我们可以发现,对于经常出现的数据(i代表数据类别),其梯度累积的越大,而对于出现频次很小的数据,梯度累积就很小,这就保证了在出现次数较少的数据上更新的幅度大一些,在出现频次较大的数据上更新的更慢一些,并且随着时间的推移,学习率逐渐在衰减。因此AdaGrad可以做到自适应的改变学习率来调控参数更新。
Adam:
这个方法就比较牛逼了,如果在深度学习中你拿不住哪个优化器更好,那就选它吧。Adam将结合了梯度的一阶矩和二阶矩,一方面通过梯度一阶矩为梯度下降提供了动量,另一方面通过梯度二阶矩提高环境的感知能力,可以自适应的调控学习率使其更快的收敛到全局最优(也可能是局部最优),Adam的计算公式为:

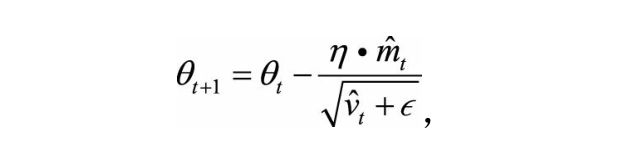
其中β 1 ,β 2 为衰减系数,m t 是一阶矩,v t 是二阶矩。这里对m与v进行了偏置矫正。
Adam使用了一种滑动窗口内求平均的思想,时间久远的梯度对当前的平均值的贡献以指数的方式进行衰减。当m较大,v较大时,梯度下降平稳,这意味着当前正处于一个大坡的环境。当m较小,v较大时,此时可能正处于“峡谷”地带,有可能陷入局部最小值。当m较大,v较小时,这不可能出现。当m较小,v也较小时,算法可能基本收敛,但是也可能到达了“平坦”区。
正则化
正则化在机器学习中主要使用的是L2正则化和L1正则化,它们虽然都起到正则化的左右,但是对参数的处理效果却大相径庭。
为什么需要正则化?
在机器学习中(或深度学习)有些模型过于复杂导致模型训练阶段产生过拟合(训练集的损失和准确率与验证集的损失和准确率相差很大)。过拟合是指模型的学习能力太强了,将一些噪音点和数据的复杂规律都学到了,但这却降低了模型的泛化能力。为了避免过拟合,正则化是一种十分有效的手段。
什么是正则化?
正则化就是对参数进行削减,可以从参数量和参数大小两个角度出发。
L1正则化与L2正则化的区别
解释1:解空间形状
事实上,带有正则化的损失函数与带有约束项的损失函数是等价的。为了约束w的可能取值空间从而防止过拟合,我们为该最优化问题加上一个约束,就是w的L2范数的平方不能大于m:
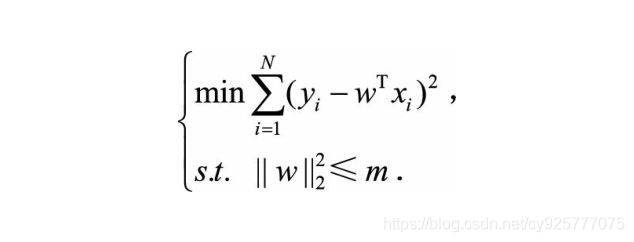
为了求解带约束条件的凸优化问题,写出拉格朗日函数
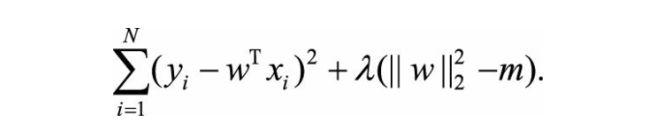
对上述拉格朗日方程的w求偏导,你会得到和对带有正则化的损失函数求偏导一样的结果,不信你试试。
将正则化问题转化为带有约束条件的优化问题就很容易理解了,直接上图,
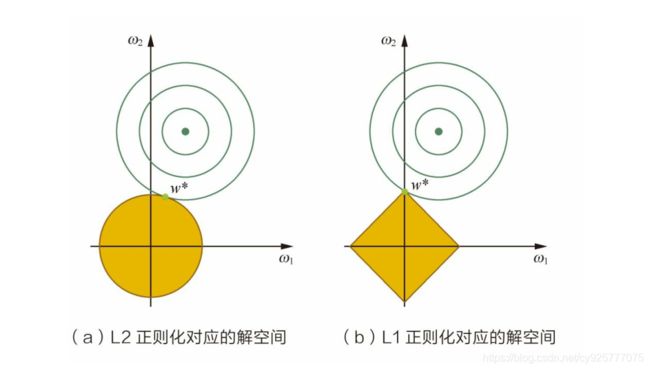
图中等高线是我们的优化目标,黄色区域是我们的约束区域,很容易发现如果原问题目标函数的最优解不是恰好落在解空间内,那么约束条件下的最优解一定是在解空间的边界上,而L1“棱角分明”的解空间显然更容易与目标函数等高线在角点碰撞,从而产生稀疏解。
解释2:损失函数曲线
第二个角度试图用更直观的图示来解释L1产生稀疏性这一现象。仅考虑一维的情况,多维情况是类似的,如图所示。假设棕线是原始目标函数L(w)的曲线图,显然最小值点在蓝点处,且对应的w * 值非0。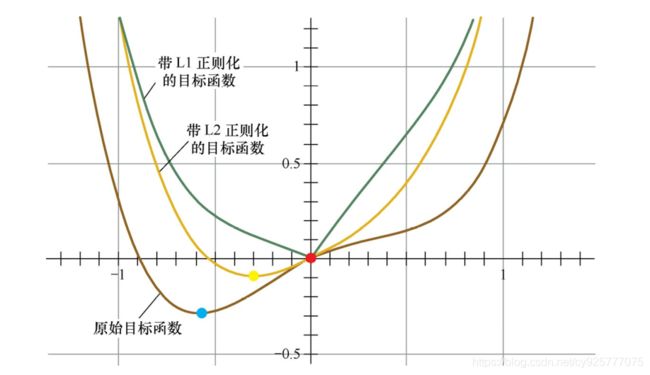
首先,考虑加上L2正则化项,目标函数变成L(w)+Cw 2 ,其函数曲线为黄色。此时,最小值点在黄点处,对应的w * 的绝对值减小了,但仍然非0。
然后,考虑加上L1正则化项,目标函数变成L(w)+C|w|,其函数曲线为绿色。此时,最小值点在红点处,对应的w是0,产生了稀疏性。
产生上述现象的原因也很直观。加入L1正则项后,对带正则项的目标函数求导,正则项部分产生的导数在原点左边部分是−C,在原点右边部分是C,因此,只要原目标函数的导数绝对值小于C,那么带正则项的目标函数在原点左边部分始终是递减的,在原点右边部分始终是递增的,最小值点自然在原点处。相反,L2正则项在原点处的导数是0,只要原目标函数在原点处的导数不为0,那么最小值点就不会在原点,所以L2只有减小w绝对值的作用,对解空间的稀疏性没有贡献。
