机器学习（3）高斯判别分析&朴素贝叶斯分类器

判别模型与生成模型

判别模型

判别模型是对观测数据进行直接分类，常见的判别模型有逻辑回归和感知机算法等。此模型仅对数据进行分类，并不能具象化或者量化数据本身的分布状态，因此也无法根据分类生成可观测的图像。

生成模型

与判别模型不同，生成模型首先了解数据本身分布情况，并进一步根据输入 x，给出预测分类 y 的概率。该模型有着研究数据分布形态的概念，可以根据历史数据生成新的可观测图像。
贝叶斯分类就是一个典型的例子。在这个例子中，我们有一个先验分类，根据这个先验分类，我们可以使用贝叶斯公式计算每个分类的概率，然后取概率最高的概率。同时，我们还可以根据特定的先验生成特征，这就是一个生成过程。

高斯判别分析简介

高斯判别分析（GDA），是拟定数据符合高斯分布，并利用这一假定，使用观测数据估计参数，并使用这一模型预测未知类别数据属于哪类对应的高斯分布，从而推断其类别。
在介绍了判别模型与生成模型的区别后，我们可以知道，高斯判别分析（GDA）就是一个生成模型。因为，我们有一个先验假设：即单个类别的数据分布都符合高斯分布（正态分布）。

贝叶斯公式

在介绍高斯判别分析之前，我们先将贝叶斯公式写在这里，后面我们就会看到贝叶斯公式在分类问题中的应用。
$$P(A_i|B)=\frac{P(A_i)P(B|A_i)}{{\sum }_{i=1}^{c}P(A_i)P(B|A_i)}$$
可以看到，等式左边是B情况下A的条件概率；等式右边，分母是B的先验概率，分子是A的先验概率与A情况下B条件概率的乘积。这个形式相当优美。
贝叶斯公式常常用于在拿到实验结果后推断概率的分布，因为等式右边常常是我们关心的需要估测的$P(A_i|B)$。
有关更多贝叶斯公式的介绍，请参看贝叶斯公式，该条目中给出了一个吸毒者检测的例子，以利于读者理解。

高斯分布

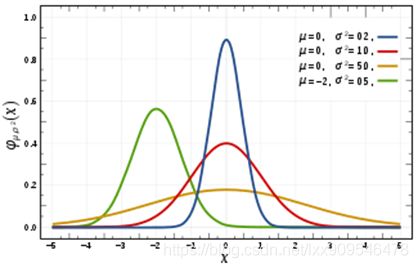
上图是一个一维高斯分布，其概率密度函数为：
$$N(X|\mu ,{\sigma }^2)=\frac{1}{(2\pi {\sigma }^2{)}^{\frac{1}{2}}}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$
多维数据的高斯分布密度函数为：
$$N(X|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{D}{2}}|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(X-\mu {)}^T{\Sigma }^{-1}(X-\mu )}$$

高斯判别分析过程

在贝叶斯公式$$P(Y_i|X)=\frac{P(Y_i)P(X|Y_i)}{{\sum }_{i=1}^{c}P(Y_i)P(X|Y_i)}$$中，我们将A看做变量的类别，B看做变量的取值。
这种情况下，我们就将贝叶斯公式应用在了目标为预测变量类别的问题中。
我们可以对变量类别所可取的所有值$A_i$都计算条件概率$P(A_i|B)$，这样我们只需取概率最大的类别即可当做其类别的预测。
即$$Y_T=\underset{Y_i}{\mathrm{argmax}}P(Y_i|X)$$
我们发现，对于每个类别，需要计算贝叶斯公式分母都相同，因此上式等价于
$$Y_T=\underset{Y_i}{\mathrm{argmax}}P(Y_i)P(X|Y_i)$$
上式中，$P(Y_i)$很容易计算，但$P(X|Y_i)$并非看上去那么容易。
在数据的值是离散的标签时，我们很容易计算出$P(X|Y_i)$，但对于连续值则并非如此。也就是说，我们需要对于在样本中未出现过的数据为其估计一个概率。
这样做可以采用的一种方法是：
假定数据复合某种连续的分布，这样我们就能为某个未出现过的连续值估计一个概率了。
最常用的连续分布即高斯分布（正态分布），因此我们常假定上述数据符合高斯分布，从而为数据估计出一个概率$P(X|Y_i)$。

这样，我们为每一个类别模拟一个高斯分布
$$N(X|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{D}{2}}|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(X-\mu {)}^T{\Sigma }^{-1}(X-\mu )}$$
其中，上式中的参数$\mu ,\Sigma$都由最大似然估计给出。
这样，我们就可以由类别和未在样本集中出现的观测数据，为其指定一个概率。

下式$$Y_T=\underset{Y_i}{\mathrm{argmax}}P(Y_i)P(X|Y_i)$$
中的两部分我们都可以进行计算了，因此我们只需对每个类别进行计算然后选出概率最大对应的类别，就是我们预测的该数据对应的类别。

至此，我们的问题似乎已经得到了解决。
但请考虑下面的情况：
B并不是单个属性的取值，而是多个属性的组合。如果我们只用对应条件的组合当做样本，那么则会出现稀疏的情况。
也即，符合这样的情况实在太少，但事实上，部分符合条件的样本本身就能为我们的推断带来一定的信息。
举例：
我们要预测一个同时有心律不齐以及高血压以及家族有心脑血管病家族史的人的未来患病情况。
在病患数据不足的情况下，可能同时具有上述三个属性的病例不多，但符合单个的病例数应该还不少，这样的数据足以为我们提供一些信息。

为了解决这样的问题，我们将引入朴素贝叶斯分类器。

朴素贝叶斯分类器

概述

朴素贝叶斯是一种构建分类器的简单方法。该分类器模型会给问题实例分配用特征值表示的类标签，类标签取自有限集合。它不是训练这种分类器的单一算法，而是一系列基于相同原理的算法：所有朴素贝叶斯分类器都假定样本每个特征与其他特征都不相关。
尽管是带着这些朴素思想和过于简单化的假设，但朴素贝叶斯分类器在很多复杂的现实情形中仍能够获取相当好的效果。
接着我们谈谈“朴素贝叶斯”之所以“朴素”的原因，这来源于我们假定的特征条件独立假设，该条件假定数据中的几个属性彼此独立、互不影响。

公式

刚刚我们在使用贝叶斯公式的用于单属性分类器的形式如下：
$$Y_T=\underset{Y_i}{\mathrm{argmax}}P(Y_i)P(X|Y_i)$$
由于上面提到的特殊情况，我们的分类器并不能很好解决这样多标签组合的问题，但有了特征条件独立假设，我们就可以尝试来做这件事。
由于条件独立假设，联合概率等于边缘概率的乘积
$$P(Y|X)=\frac{P(Y)\times \prod _{i=1}^{d}P(X_i|Y)}{P(X)}$$
同样的，由于分母相同，问题又转变成了：
$$Y_T=\underset{Y_i}{\mathrm{argmax}}P(Y_i)\prod _{j=1}^{d}P(X_j|Y_i)$$
对于离散值的情况，每个种类中每个标签的概率$P(X_j|Y_i)$，可以使用频率估计出来。也就是说，虽然我们不一定有标签组合的指定类别，但我们可以通过各属性的乘积来计算，因此，我们就使用了特征独立假设成功解决了上面的属性组合问题。

拉普拉斯平滑

拉普拉斯平滑是为了克服某类未出现在训练集中，而出现的0概率事件，而可以预见的，由于概率连乘，一旦乘数中出现一个0，整个概率就为0，因此我们使用拉普拉斯平滑来处理上面的情况。
$$P(X=x|Y=y)=\frac{{\sum }_{i=1}^{N}I(X=x,Y=y)+\lambda }{{\sum }_{i=1}^{N}I(Y=y)+K\lambda }$$
拉普拉斯平滑中，$\lambda$取1，其中K是该属性的取值个数。
值得注意的是，这样的情况只会发生在离散值的情况下，对于连续值，我们会使用高斯分布估计它的概率。

高斯朴素贝叶斯

上面讨论的，都是属性是离散值的情况。但对于连续值，我们有必要使用高斯分布来估计它的概率。

对于概率$P(X_j|Y_i)$，当$X$取值为连续值时，我们可以使用高斯分布来估计这个概率$$Y_T=\underset{Y_i}{\mathrm{argmax}}P(Y_i)\prod _{j=1}^{d}P(X_j|Y_i)$$
最终将变成多个属性上高斯分布估计概率的连乘再乘以先验概率的值，算出各个类别的这个值，然后取概率最大对应的类别作为估计出的类别。

小结

至此我们已经讨论了利用贝叶斯公式处理连续值与离散值的分类问题。

我们来尝试理一下高斯朴素贝叶斯与其他模块的关系：

• 高斯朴素贝叶斯是朴素贝叶斯分类器在遇到连续值属性的特殊情况
• 高斯朴素贝叶斯是高斯判别分析加上特征独立假设的特殊情况

如果D个维度之间相互独立,那么多元高斯分布就可以表示成单高斯分布概率密度函数的连乘积。

我们使用朴素贝叶斯来估计后验概率，通过比较后验概率来实现不同类的分类，该方法可适用于多分类问题。
一个特殊情况，对于离散值与连续值混合的问题，我们采用了两种策略来解决：

• 连续数据离散化
• 用高斯分布估计概率密度

同时，在离散值的预测中，会遇到因训练集过小导致的某个类频率为0的问题，我们用频率来估计概率，因此得到的概率也为0，连乘时得到的最终概率也是0。这样显然不是一个公平的决策方式，因此我们使用了拉普拉斯平滑技巧来避免0概率。