【机器学习】关联规则及python实现
简介
关联分析是一种在大型数据库中发现变量之间的有意义的关系的方法。这种关系表现为两种形式:频繁项集和关联规则。关联分析的目的是利用一些度量来识别数据库中的强规则。数学定义:
假设 I = { I 1 , I 2 , … , I m } {\displaystyle I=\{I_{1},I_{2},\ldots ,I_{m}\}} I={I1,I2,…,Im}是项的集合。给定一个交易数据库 D = { t 1 , t 2 , … , t n } {\displaystyle D=\{t_{1},t_{2},\ldots ,t_{n}\}} D={t1,t2,…,tn},其中每个事务 t t t是 I I I的非空子集,即 t ⊆ I {\displaystyle t\subseteq I} t⊆I,每一个交易都与一个唯一的标识符TID(Transaction ID)对应。关联规则是形如 X ⇒ Y {\displaystyle X\Rightarrow Y} X⇒Y的蕴涵式,其中 X , Y ⊆ I {\displaystyle X,Y\subseteq I} X,Y⊆I且 X ∩ Y = ∅ {\displaystyle X\cap Y=\emptyset } X∩Y=∅, X {\displaystyle X} X和 Y {\displaystyle Y} Y分别称为关联规则的先导(antecedent或left-hand-side, LHS)和后继(consequent或right-hand-side, RHS) 。关联规则 X ⇒ Y {\displaystyle X\Rightarrow Y} X⇒Y在 D D D中的支持度(support)是 D D D中事务包含 X ∪ Y {\displaystyle X\cup Y} X∪Y的百分比,即概率 P ( X ∪ Y ) {\displaystyle P(X\cup Y)} P(X∪Y);置信度(confidence)是包含 X X X的事务中同时包含 Y Y Y的百分比,即条件概率 P ( Y ∣ X ) {\displaystyle P\left(Y|X\right)} P(Y∣X)。如果同时满足最小支持度阈值和最小置信度阈值,则认为关联规则是有趣的。这些阈值由用户或者专家设定。(引自wikipedia)
基本概念
为了说明概念,我们以购物篮分析为例,即假设我们的数据是由若干购物清单构成的列表,每个购物清单由若干商品组成:
d a t a = [ [ i t e m 11 , i t e m 12 , . . . ] , [ i t e m 21 , i t e m 22 , . . . ] , [ i t e m 31 , i t e m 32 , . . . ] , . . . ] data = [[item_{11}, item_{12}, ...], [item_{21}, item_{22}, ...], [item_{31}, item_{32}, ...], ...] data=[[item11,item12,...],[item21,item22,...],[item31,item32,...],...]
- 事务
数据中每个样本称为事务,在我们的例子中 [ i t e m 11 , i t e m 12 , . . . ] [item_{11}, item_{12}, ...] [item11,item12,...]就是一个事务 - 项
事务中的元素称为项,在我们的例子里即每个购物清单中的商品 i t e m i j item_{ij} itemij都是一项 - 项集
由项组成的集合称为项集,显然项集包含于事务,根据项集包含的项的数目可以记为n-项集;例如在我们的例子中 { i t e m 21 , i t e m 22 } \{item_{21}, item_{22}\} {item21,item22}可以构成一个2-项集 - 关联规则
形如 X ⇒ Y {\displaystyle X\Rightarrow Y} X⇒Y的蕴涵式,其中 X X X, Y Y Y都是项集,分别称为先导和后继 - 支持度(support)
定义 σ ( X ) \sigma(X) σ(X)表示包含X的事务的数量, N N N表示事务的总数,则:
s u p p o r t ( A ⇒ C ) = σ ( A ∪ C ) / N {support(A\Rightarrow C) = \sigma(A\cup C)/N} support(A⇒C)=σ(A∪C)/N
取值范围: [ 0 , 1 ] [0, 1] [0,1]
支持度反映了 A A A与 C C C同时出现的概率。如果 A A A与 C C C同时出现的概率很小,说明 A A A与 C C C的关系不大;如果 A A A与 C C C同时出现的非常频繁,则说明 A A A与 C C C很可能是相关的 - 置信度(confidence)
c o n f i d e n c e ( A ⇒ C ) = s u p p o r t ( A ∪ C ) / s u p p o r t ( A ) = σ ( A ∪ C ) / σ ( A ) confidence(A\Rightarrow C) = support(A\cup C) / support(A) =\sigma(A\cup C)/\sigma(A) confidence(A⇒C)=support(A∪C)/support(A)=σ(A∪C)/σ(A)
取值范围: [ 0 , 1 ] [0, 1] [0,1]
置信度反映了关联规则的可信度:购买了项集 A A A中的商品的顾客同时也购买了项集 C C C中商品的可能性有多大 - 提升度(lift)
l i f t ( A ⇒ C ) = c o n f i d e n c e ( A ⇒ C ) / s u p p o r t ( C ) lift(A\Rightarrow C) = confidence(A\Rightarrow C) / support(C) lift(A⇒C)=confidence(A⇒C)/support(C)
取值范围: [ 0 , ∞ ) [0, \infty) [0,∞)
提升度反映了 A A A的出现对 C C C的出现概率的提升作用,提升度小于等于1时表示关联规则是无效的,反之提升度越大则表明 A A A对 C C C的提升程度越大,也表明关联性越强 - 杠杆率(leverage)
l e v e r a g e ( A ⇒ C ) = s u p p o r t ( A ⇒ C ) − s u p p o r t ( A ) ∗ s u p p o r t ( C ) leverage(A\Rightarrow C) = support(A\Rightarrow C) - support(A)*support(C) leverage(A⇒C)=support(A⇒C)−support(A)∗support(C),
取值范围: [ − 1 , 1 ] [-1, 1] [−1,1]
杠杆率反映了当先导项与后继项独立分布时,先导项与后继项一起出现的次数比预期多多少 - 确信度(conviction)
c o n v i c t i o n = ( 1 − s u p p o r t ( C ) ) / ( 1 − c o n f i d e n c e ( A ⇒ C ) ) conviction = (1 - support(C)) / (1 - confidence(A\Rightarrow C)) conviction=(1−support(C))/(1−confidence(A⇒C))
取值范围: [ 0 , ∞ ) [0, \infty) [0,∞)
与提升度类似,但用差值表示 - 频繁项集
支持度大于给定阈值的项集称为频繁项集
相关算法
Apriori algorithm(先验算法)
先验算法用于搜索数据库中的频繁项集,其核心思想为:如果一个项集是非频繁项集,那么它的所有超集也是非频繁项集,从而达到剪枝的目的。算法流程:
- 生成所有1-项集构成项集列表
- 对项集列表中的项集逐个计算支持度,如果大于给定的阈值则将它放入频繁项集,反之放入非频繁项集
- 用频繁项集生成项数+1的项集(比如当前项集列表中都是2-项集,则这一步就生成3-项集),生成的新项集要保证不包含非频繁集中的任意一个项集(否则它就是一个非频繁项集的超集,根据简单的推理可知这个项集也是非频繁的),将这些新项集放入临时项集列表
- 如果临时项集列表非空,则用临时项集列表更新原项集列表,并跳转到第2步,否则结束循环
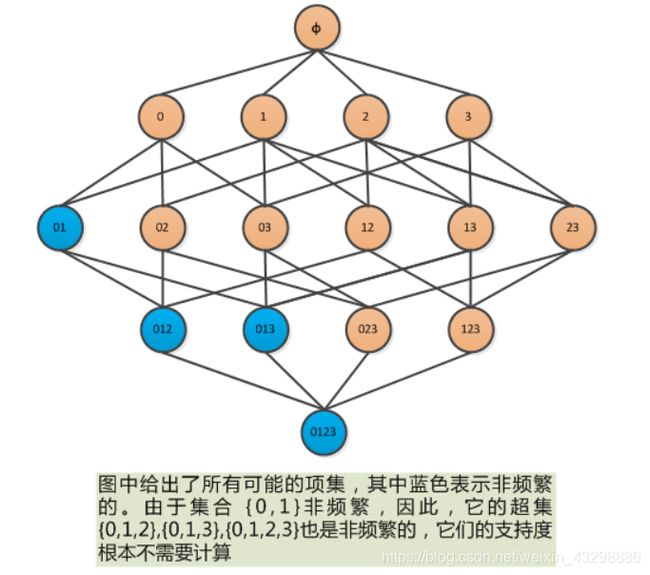
图片来源:90Zeng的博客
FP-growth算法
参考刘建平Pinard的博客
Python实现
mlxtend包已经封装了以上算法,我们只要安装这个包就可以对数据进行关联分析了
安装包
命令行执行pip install mlxtend
mlxtend.preprocessing.TransactionEncoder
这个类用于对我们的数据进行编码;由于源数据一般是字符串列表,我们需要转换为multi-hot的编码形式才能进一步处理,用法见示例
mlxtend.frequent_patterns.apriori
Apriori算法,它有以下参数:
min_support:最小支持度,默认0.5use_colnames:是否显示项的原始名称,默认为False,此时输出的项是编码后的数字max_len:频繁项集最大长度,默认为False ,即生成所有频繁项集verbose:控制迭代过程中的输出,默认为0low_memory:是否以低内存占用的模式运行算法,默认为False;若设为True将导致算法耗时变长,慎用
mlxtend.frequent_patterns.fpgrowth
FP-growth算法,它有以下参数:
min_support:最小支持度,默认0.5use_colnames:是否显示项的原始名称,默认为False,此时输出的项是编码后的数字max_len:频繁项集最大长度,默认为False ,即生成所有频繁项集verbose:控制迭代过程中的输出,默认为0
示例代码
from mlxtend.frequent_patterns import association_rules
from mlxtend.frequent_patterns import apriori
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
purchases = [['Milk', 'Broccoli', 'Sauce', 'Beef', 'Eggs', 'Yogurt'],
['Wine', 'Broccoli', 'Sauce', 'Beef', 'Eggs', 'Yogurt'],
['Milk', 'Apple', 'Beef', 'Eggs'],
['Milk', 'Fish', 'Corn', 'Beef', 'Yogurt'],
['Corn', 'Broccoli', 'Broccoli', 'Beef', 'Banana', 'Eggs']]
te = TransactionEncoder()
te_array = te.fit(purchases).transform(purchases)
df = pd.DataFrame(te_array, columns=te.columns_)
print(df)
# 采用apriori算法生成频繁项集
frequent_itemsets = apriori(df, min_support=0.6, use_colnames=True)
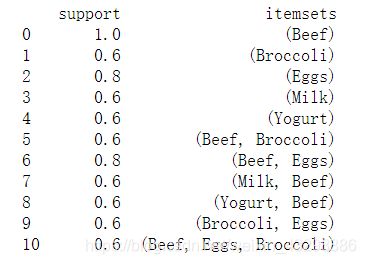
print(frequent_itemsets)
frequent_itemsets['length'] = frequent_itemsets['itemsets'].apply(lambda x: len(x))
rules = association_rules(frequent_itemsets, metric='lift', min_threshold=1)
# 选取提升度大于1且置信度大于0.5的关联规则
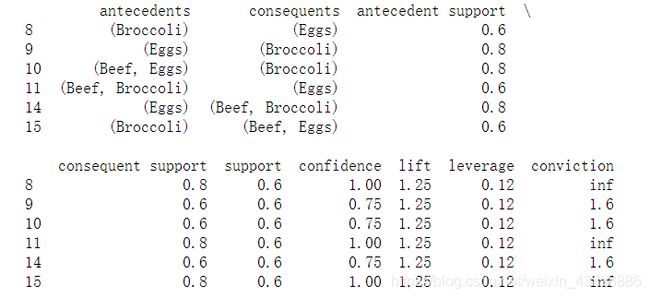
print(rules[(rules['lift'] > 1) & (rules['confidence'] > 0.5)])
当数据集中商品种类很多而交易很少时,可以使用稀疏矩阵存储交易信息以节省内存:
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori
te = TransactionEncoder()
oht_ary = te.fit(dataset).transform(dataset, sparse=True)
sparse_df = pd.DataFrame.sparse.from_spmatrix(oht_ary, columns=te.columns_)
apriori(sparse_df, min_support=0.6, use_colnames=True, verbose=1)