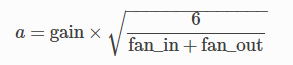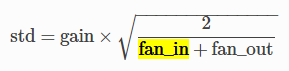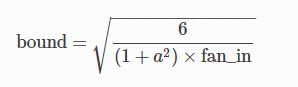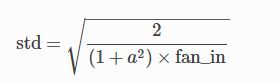深度学习基础知识（一）--- 权重初始化

1、为什么需要权重初始化？

① 为了使神经网络在合理的时间内收敛

② 为了尽量避免在深度神经网络的正向（前向）传播过程中层激活函数的输出梯度出现爆炸或消失。

 

2、如何进行初始化？

①如果将每个隐藏单元的参数都初始化为0

那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值，并传递至输出层。在反向传播中，每个隐藏单元的参数梯度值相等。因此，这些参数在使用基于梯度的优化算法迭代后值依然相等。这样所有隐层的单元都是对称的了，很难学到什么有效的信息，之后的迭代也是如此。

所以权重初始化不能将权重参数全部初始化为0，应打破这种对称性。

②如果将参数都初始化为0周围极小的值：

也不好，比如如果用sigmoid做激活函数，它在0周围是近似线性的，如果我们的参数都初始化为0附近，那么可能数据经过神经元之后，大部分都落在线性区，那么我激活函数引入非线性的作用将被削减。

③如果参数都初始化为较大的值，很显然容易使得输出落入饱和区。

 

所以合理的初始化时比较重要的，一般采用随机的初始化。

 

3、常见的几种初始化方式

①、均匀分布初始化：

将参数初始化为 均匀分布U(a,b) 上的随机值，pytorch的实现方案：

torch.nn.init.uniform_(tensor, a=0, b=1)

②、高斯初始化：

将参数初始化为 高斯分布N(0,1) 上的随机值，pytorch的实现方案：

torch.nn.init.normal_(tensor, mean=0, std=1)

③、常数初始化：

将参数初始化为一个 固定的常数val, pytorch实现方案为：

torch.nn.init.constant_(tensor, val)

上面三种初始化方法其实并不是十分理想的初始化方案，因为如果网络层数过深的话，

依然会导致 梯度爆炸 或者 梯度弥散的情况出现，

一般在使用中，可能就是神经网络 中的某一两层可能会用到上述初始化方案，比如自己写的某几层

并不建议对所有的参数都使用上述初始化方案

 

4、Xiaver 初始化方案

Xavier初始化的基本思想是，若对于一层网络的输入和输出的方差尽量不变，

这样就可以避免输出趋向于0，从而避免梯度弥散情况。

参考资料：

https://prateekvjoshi.com/2016/03/29/understanding-xavier-initialization-in-deep-neural-networks/

http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf

https://zhuanlan.zhihu.com/p/64464584

https://zhuanlan.zhihu.com/p/40175178

pytorch的实现方案①：torch.nn.init.xavier_uniform_(tensor, gain=1)

将参数初始化为均匀分布 U(-α, α) 上的随机值，其中 α 取值为：

fan_in 指输入端神经元的个数， fan_out指输出端神经元的个数，它会自己根据网络计算。

gain 是一个增益， 默认为1；

pytorch的实现方案②：torch.nn.init.xavier_normal_(tensor, gain=1)

将参数初始化为高斯分布 N(0, std^2) 上的随机值，而std的取值是：

5、Kaiming初始化方案

Kaiming初始化基本思想是，当使用ReLU做为激活函数时，Xavier的效果不好，

原因在于：当ReLU的输入小于0时，其输出为0，影响了输出的分布模式。

也就是激活函数输出均值不为0，我们上面的推导中是有假设E(X)=0的

 

因此Kaiming He初始化，在Xavier的基础上，假设每层网络有一半的神经元被关闭，于是其分布的方差也会变小。所以提出一个新的假设，那就是前向传播中，如果采用Xiaver，方差会缩小为原来一半，那么为了修正这个缩减，就使得参数初始化的范围比原来扩大一倍

（如果理解有误，欢迎指正，提前谢过）

pytorch实现方案①：

torch.nn.init.kaiming_uniform_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

将参数初始化为均匀分布U(-bound, bound)上的随机值，其中 bound 取值为：

α：该层后面一层的激活函数中负的斜率 (0 for ReLU by default)

 

mode : ‘fan_in’ (default) 或者‘fan_out’.

使用fan_in保持weights的方差在前向传播中不变；

使用fan_out保持weights的方差在反向传播中不变。

 

pytorch实现方案②：

torch.nn.init.kaiming_normal_(tensor, a=0, mode='fan_in', nonlinearity='leaky_relu')

将参数初始化为高斯分布N(0,std^2)上的随机值，而std的取值是：

α：该层后面一层的激活函数中负的斜率 (0 for ReLU by default)

 

mode : ‘fan_in’ (default) 或者‘fan_out’.

使用fan_in保持weights的方差在前向传播中不变；

使用fan_out保持weights的方差在反向传播中不变。

 

6. pytorch常见的 权重初始化 操作方法

方案一：直接对某层的data进行赋值

举例：

self.conv1.weight.data.normal_(0, 0.01)
self.conv1.bias.data.zero_()

方案二：调用nn初始化模块：

torch.nn.init.normal_(self.conv1.weight, std=0.01)
torch.nn.init.constant_(self.conv1.bias, 0)

可搭配for循环使用：

for layer in self.children():
    torch.nn.init.normal_(layer.weight, std=0.01)
    torch.nn.init.constant_(layer.bias, 0)

方案三： 定义一个自己的小函数

def _weight_init(m):
    classname = m.__class__.__name__
    if classname.find('Conv') != -1:
        torch.nn.init.xavier_(m.weight)
        torch.nn.init.xavier_(m.bias)
    if classname.find('Linear') != -1:
        torch.nn.init.normal_(m.weight, std=0.01)
        torch.nn.init.constant_(m.bias, 0)

#或者不读取下划线，直接看是不是某个类,这种方法相对来说更安全一些
def _weights_init(m):
    if isinstance(m, torch.nn.Conv2d):
        torch.nn.xavier_(m.weight)
        torch.nn.xavier_(m.bias)
    if isinstance(m, torch.nn.Linear):
        torch.nn.init.normal_(m.weight, std=0.01)
        torch.nn.init.constant_(m.bias, 0)

然后对某个Net应用：
Net.apply(_weight_init)

以上三个均为示例，具体使用情况请依据自己的网络和具体的代码，请勿生搬硬套。