2021美国大学生数学建模竞赛D题

题目

（仅作为记录留念)

问题

解决方法

音乐是人类文化遗产的一部分，并在集体经验中扮演着重要的角色。本文的目标是建立一个衡量音乐影响力的模型来审视艺术家和流派的进化和革命趋势。

在任务1中，我们建立了一个有向的音乐影响力网络，其中影响者与追随者作为节点并且用边的权重来衡量影响力的强弱。我们通过捕捉网络的聚类系数、特征向量中心性以及中间中心性三个参数来衡量每一位音乐家在网络中的中心程度、长期影响力以及重要程度。

在任务2中，我们建立了基于模糊C均值聚类算法的音乐相似性度量模型。我们以隶属度作为音乐相似性度量的指标，最终我们得到结论：同一类型的艺术家可能比不同类型的艺术家更相似。

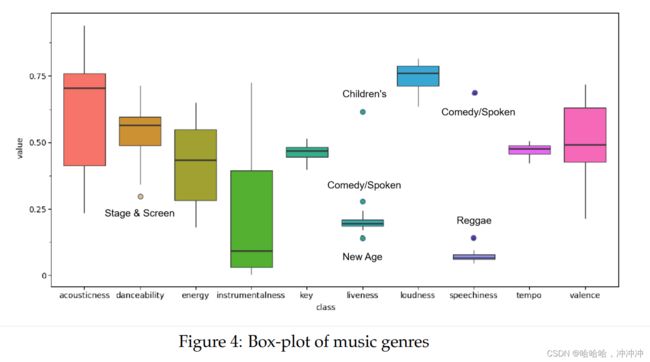
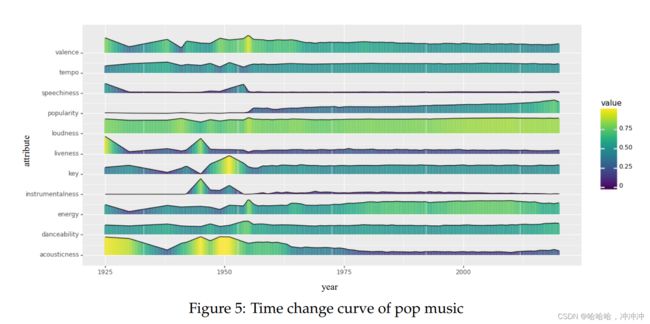
在任务3中，首先，我们对full_music_data数据集中的异常数据进行了清洗，并统计了19种音乐派别不同音乐属性，通过箱型图的离群值直观得出了不同类型的区别。接着我们以流行音乐为例做具体分析得到流行音乐的各种特征随时间的变化趋势。

在任务4中，我们对音乐影响力网络中的边的权重(影响力)与相似性指标进一步修正，通过设计基于深度优先搜索的异常点检测算法得到网络中影响力很大但是相似性却很小的节点，并由此来判别影响者是否真的会影响追随者创作的音乐。

在任务5中，我们首先设计了随时间动态变化的合作者网络，其中节点代表至少有过一次合作机会的音乐家。接着我们通过设立指标为每一个网络节点定义属性并使用Gephi计算得到相邻时间段内的合作者网络中的最具影响力节点集，并将节点集判定为最具影响力音乐家，将重心的变化作为衡量音乐发生重大转变的特征。

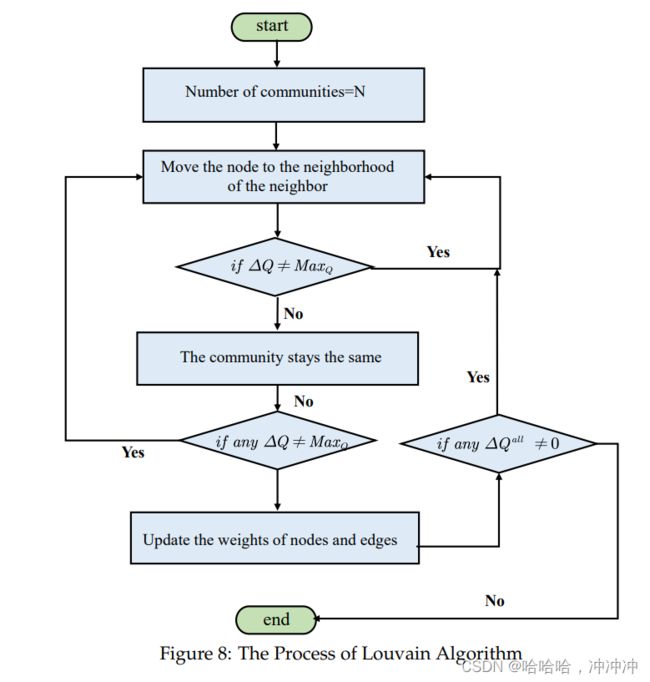
在任务6中，本文选用流行音乐作为研究对象，通过Louvain算法检测出合作者网络中的不同社区，进而得到随时间变化的5种不同音乐风格的社区。我们通过对网络节点度分析得出结论：艺术家的影响力会随着时间的推移越来越集中于少部分目前节点度较大(影响力较大)的艺术家身上。

在任务7中，本文选用音乐家之间的相似性指标与观众欢迎度作为度量音乐文化影响的指标，并通过定义网络中节点对应的熵的变化速率来识别社会、政治或技术变革(如互联网)的影响程度。
在最后我们进行了灵敏性分析以获得对我们模型的深入理解，此外我们还分析了我们模型的优缺点。

好看一点的图

主要画图的Code

#雷达图
'''
import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt
path="./data3.csv"
data1 = pd.read_csv(path)
data1 = data1[data1["class"]!="Unknown"]
'''


import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from math import pi
from matplotlib.pyplot import figure, show, rc 
plt.rcParams["patch.force_edgecolor"] = True

path="./data3.csv"
data1 = pd.read_csv(path)
data1 = data1[data1["class"]!="Unknown"]
df = data1.iloc[:,3:15]
print(df.head())
data1.iloc[:,3:15] = (df - df.min()) / (df.max() - df.min())

print(data1["year"].min(),data1["year"].max())
data1 = data1[data1["year"]>=1980] 
data1 = data1[data1["year"]<=2000]
#print(data1.head())
col = np.array(data1.columns) 
indexx = col[[3,4,5,6,7,10,11,12,13]]

print(indexx)
#dataA = data1[data1["class"]=='Pop/Rock'][indexx].mean()
#dataB = data1[data1["class"]=='Classical'][indexx].mean()

dataA = data1[data1["class"]=='Pop/Rock'][indexx].mean()
dataB = data1[data1["class"]=='Classical'][indexx].mean()
#dataC = data1[data1["class"]=='Blues'][indexx].mean()


'''
df = pd.DataFrame(dict(categories=['var1', 'var2', 'var3', 'var4', 'var5'],
                       group_A=[38.0, 29, 8, 7, 28],
                       group_B=[1.5, 10, 39, 31, 15]))
'''

df = pd.DataFrame(dict(categories=indexx,
                       group_A=dataA,
                       group_B=dataB))

print(df.head())
N = df.shape[0]
 
angles = [n / float(N) * 2 * pi for n in range(N)]
angles += angles[:1]

fig = figure(figsize=(4,4),dpi =90)  
ax = fig.add_axes([0.1, 0.1, 0.6, 0.6], polar=True)

ax.set_theta_offset(pi / 2)
ax.set_theta_direction(-1)
ax.set_rlabel_position(0)

plt.xticks(angles[:-1], df['categories'], color="black", size=10)
plt.ylim(0,1)
plt.yticks(np.arange(0,1,0.2),color="black", size=8,verticalalignment='center',horizontalalignment='right')

plt.grid(which='major',axis ="x", linestyle='-', linewidth='0.5', color='gray',alpha=0.5)
plt.grid(which='major',axis ="y", linestyle='-', linewidth='0.5', color='gray',alpha=0.5)

values=df['group_A'].values.flatten().tolist()
values += values[:1]
ax.fill(angles, values, '#7FBC41', alpha=0.3)
ax.plot(angles, values, marker='o', markerfacecolor='#7FBC41', markersize=4, color='k', linewidth=0.25,label="Pop/Rock influencer")

values=df['group_B'].values.flatten().tolist()
values += values[:1]
ax.fill(angles, values, '#C51B7D', alpha=0.3)
ax.plot(angles, values, marker='o', markerfacecolor='#C51B7D', markersize=4, color='k', linewidth=0.25,label="Classical follower")

'''
values=df['group_C'].values.flatten().tolist()
values += values[:1]
ax.fill(angles, values, '#FFFF00', alpha=0.3)
ax.plot(angles, values, marker='o', markerfacecolor='#FFFF00', markersize=4, color='k', linewidth=0.25,label="Blues")
'''



plt.legend(loc='upper left',bbox_to_anchor=(0.75, 1.09))

plt.show()

#峰峦图

import pandas as pd
import numpy as np
from plotnine import *
from scipy import interpolate
#df=pd.read_csv('Facting_Data.csv')



path="./data3.csv"
data1 = pd.read_csv(path)
data1 = data1[data1["class"]!="Unknown"]

df = data1.iloc[:,3:17]
print(df.head())
data1.iloc[:,3:17] = (df - df.min()) / (df.max() - df.min())

data1 = data1[data1["class"]=='Pop/Rock']
'''
['Pop/Rock', 'Electronic', 'Reggae', 'Country',
 'Comedy/Spoken', 'R&B;', 'Classical', 'Latin',
  'Jazz', 'Vocal', 'Folk', 'Easy Listening', 'International',
   'Avant-Garde', 'Blues', 'Stage & Screen', 'New Age', 'Religious', "Children's"]
'''
df = data1.iloc[:,[17,16,3,4,5,6,7,9,10,11,12,13]]
#df = data1.iloc[:,[17]]
print(df.head())
df = df.groupby('year').mean()
df["year1"] = df.index 
print(df)






df_melt=pd.melt(df,id_vars='year1',var_name='var',value_name='value')
mydata=pd.DataFrame( columns=['x','y','var'])       
list_var=np.unique(df_melt['var'])
N=300
for i in list_var:
    x=df.loc[:,'year1']
    y=df.loc[:,i]
    f = interpolate.interp1d(x,y)#, kind='slinear')#kind='linear', 
    x_new=np.linspace(np.min(x),np.max(x),N)
    y_new=f(x_new)
    mydata = mydata.append(pd.DataFrame({'x': x_new,'y':y_new,'var':np.repeat(i,N)}))

height=1.1
mydata['var']=mydata['var'].astype(pd.CategoricalDtype(categories= np.unique(df_melt['var']),ordered=True))
mydata['spacing']=mydata['var'].values.codes*height

labels=np.unique(df_melt['var'])
breaks=np.arange(0,len(labels)*height,height)

base_plot=(ggplot())
for i in np.unique(df_melt['var'])[::-1]:
    mydata_temp=mydata[mydata['var']==i]
    base_plot=(base_plot+
               geom_linerange(mydata_temp,aes(x='x',ymin='spacing',ymax='y+spacing',color='y'),size=1)+
               geom_line(mydata_temp,aes(x='x',y='y+spacing'),color="black",size=0.5))
base_plot=(base_plot+scale_color_cmap(name ='Spectral_r')+
           scale_y_continuous(breaks=breaks,labels=labels)+
           guides(color=guide_colorbar(title='value'))+
           theme(dpi=100,figure_size=(6,5))) 

print(base_plot)

#箱形图
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from plotnine import *

path="./data3.csv"
data1 = pd.read_csv(path)
data1 = data1[data1["class"]!="Unknown"]
df = data1.iloc[:,3:15]
print(df.head())
data1.iloc[:,3:15] = (df - df.min()) / (df.max() - df.min())  #标准化
data1 = data1.iloc[:,[20,3,4,5,6,7,10,11,12,13]]

data1=data1.groupby('class').mean()

print(data1)
print(data1.columns)
Value = data1.values
Value =Value.T
Value = Value.reshape(Value.shape[0]*Value.shape[1])
#freq =np.logspace(1,4,num=4-1+1,base=10,dtype='int')
freq =[]
for i in range(9):
    freq.append(19)



df=pd.DataFrame({'attribute': np.repeat(data1.columns, freq), 
                 'value':Value})

box_plot=(ggplot(df,aes(x='class',y="value",fill="class"))
+geom_boxplot(show_legend=False)
+scale_fill_hue(s = 0.90, l = 0.65, h=0.0417,color_space='husl')
+theme_matplotlib()
+theme(#legend_position='none',
       aspect_ratio =1.1,
       dpi=100,
       figure_size=(4,4)))
print(box_plot)
#box_plot.save("box_plot3.pdf") 


'''
box_plot=(ggplot(df,aes(x='class',y="value",fill="class"))
+geom_boxplot(notch = True, varwidth = False,show_legend=False)
+scale_fill_hue(s = 0.90, l = 0.65, h=0.0417,color_space='husl')
+theme_matplotlib()
+theme(#legend_position='none',
       aspect_ratio =1.1,
       dpi=100,
       figure_size=(4,4)))
print(box_plot)
#box_plot.save("box_plot4.pdf") 


box_plot=(ggplot(df,aes(x='class',y="value",fill="class"))
+geom_boxplot(notch = True, varwidth = True,show_legend=False)
+scale_fill_hue(s = 0.90, l = 0.65, h=0.0417,color_space='husl')
+theme_matplotlib()
+theme(#legend_position='none',
       aspect_ratio =1.1,
       dpi=100,
       figure_size=(4,4)))
print(box_plot)
#box_plot.save("box_plot5.pdf") 


#data1.to_csv("./data4.csv",encoding='utf-8')
'''

注：数据处理使用的python的pandas库，基本上是比赛的时候现学的，所以很多变量的命名不是很规范，赛后也没来得及整理，如有兴趣可以瞧瞧，自己悟吧！
链接：https://pan.baidu.com/s/1jse5T-S2uuVCbhKlATIQrQ
提取码：snda