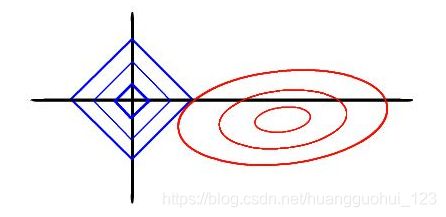
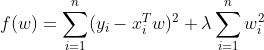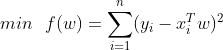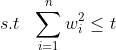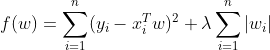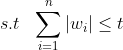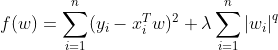机器学习——数据的共线性问题（岭回归、LASSO回归、逐步回归、主成分回归）

一、如何检验共线性

• 容忍度（Trlerance）：容忍度是每个自变量作为因变量对其他自变量进行回归建模时得到的残差比例，大小用1减得到的决定系数来表示。容忍度的值介于0和1之间，如果值越小，说明这个自变量与其他自变量间越可能存在共线性问题。
• 方差膨胀因子（Variance Inflation Factor，VIF）：VIF是容忍度的倒数，值越大则共线性问题越明显，通常以10作为判断边界。当VIF<10，不存在多重共线性；当10≤VIF<100，存在较强的多重共线性；当VIF≥100，存在严重多重共线性。
• 特征值（Eigenvalue）：实际上就是对自变量进行主成分分析，如果多个维度的特征值等于0，则可能有比较严重的共线性。
• 除此之外，还可以使用相关系数辅助判断，当相关系数R>0.8时就表示可能存在较强的相关性。

二、解决共线性的5种常用方法

要完全解决共线性问题是不可能的，我们只能解决其中严重的共线性问题，而非全部共线性问题。

1、增大样本量

通过增加样本量，来消除由于数据不足而出现的偶然共线性现象。

2、岭回归法（Ridge Regression）和LASSO回归（LASSO Regression）

岭回归分析是一种专用于多元线性回归模型共线性问题的有偏估计回归方法，实质上是一种改良的最小二乘估计法。它通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价来获得更实际和可靠性更强的回归系数。因此岭回归在存在较强共线性的回归应用中较为常用。

1）标准线性回归

我们先来回顾一下标准线性回归：

给定一组数据其中包括特征矩阵 , 目标变量向量，其中第一列为截距项，我们做线性回归是为了得到一个最优回归系数向量使得当我们给定一个的行向量能够通过预测的值。其中。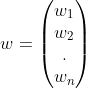

最小二乘法获取回归系数

在标准线性回归中我们需要找到是误差最小的, 即预测的值与真实的值之间的差值。

使用矩阵表示将会是的求解和程序更为简单:

将对求导可得:

【注意】

矩阵求导性质：

1）、

2）、

使其等于0，便可得到：

求得：

标准线性回归的Python实现

def std_linreg(X, Y):
    xTx = np.dot(X.T,X)
    if np.linalg.det(xTx) == 0:    #求横列式
        print('xTx is a singular matrix')   #奇异矩阵
        return
    return np.dot(np.linalg.inv(xTx),np.dot(X.T,Y))

2）岭回归（L2正则化）

如果存在较强的共线性，即中各列向量之间存在较强的相关性，会导致，从而引起对角线上的 值很大。并且不一样的样本也会导致参数估计值变化非常大。即参数估计量的方差也增大，对参数的估计会不准确。这个时候我们需要在代价函数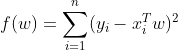上添加一个惩罚项 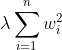，称为L2正则化。

正则化代价函数：，为岭系数。

我们希望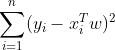尽量小，其越小，则拟合程度越高（易过拟合），模型越复杂，进而参数越多，如下图所示：

 参数越多（或者越大），则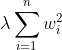越大。两者互相牵制，直到两者找到一个平衡点，这也是岭回归能够实现筛选变量，处理具有多重共线性数据的原理。

根据拉格朗日乘子法相关概念，可将上式转换为：

,其中为某个阈值。

关于拉格朗日乘子法详细解析请见【如何理解拉格朗日乘子法？ 】

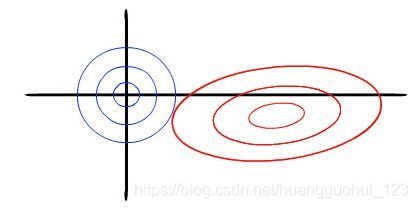
以两个自变量为例, 残差平方和可以表示为，的一个二次函数，是一个在三维空间中的抛物面，可以用等值线来表示。而限制条件， 相当于在二维平面的一个圆。这个时候等值线与圆相切的点便是在约束条件下的最优点，如下图所示，

可以得出：

• 当岭系数时，得到的解是最小二乘解
• 当岭系数趋向更大时，岭回归系数趋向于0，约束项很小

使用矩阵对正则化代价函数求解：

将对求导可得:

使其等于0，便可得到：

求得：（其中E表示单位矩阵）

岭回归的python实现方式，我们事先设定岭系数=1：

def ridge_regression(X,Y, lam=1.0):
    XTX = np.dot(X.T,X)
    m, _ = XTX.shape
    I = np.matrix(np.eye(m))   #np.eye():构建对角矩阵，默认对角1，即单位矩阵    
    return np.dot(np.linalg.inv(XTX + lam*I),np.dot(X.T,Y))

 岭系数的一般选择原则

• 各回归系数的岭估计基本稳定

• 用最小二乘法估计时符号不合理的回归系数，其岭估计的符号将变得合理

• 回归系数没有不合乎经济意义的绝对值

• 残差平方和增加不太多

 岭系数的一般选择方法

• 岭迹法

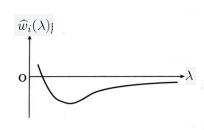
岭估计的分量作为的函数，当k在(0,] 之间变化时，在平面直角坐标系中所描绘的图像称为岭迹曲线，我们可以根据岭迹曲线的变化形状来确定适当的。常用的岭迹曲线及其显示出的相关特点如下：

在图1中，，并且比较大。这时可以将看做是对有重要影响的因素。但的图形不稳定，当从零开始略增加时，显著地下降，而且迅速趋于零，从岭系数选择的原则看，对不起作用。

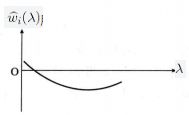
 与图1相反的情况如图2所示，，但很接近零，这时对的作用不大，但是随着略增加，骤然变为负值，从岭系数选择的原则看，对有显著的影响。

在图3中，，说明 还比较显著，但当增加时，迅速下降，且稳定为负值，这时 是对有重要影响的显著因素，从岭回归分析的角度看， 对有负影响的因素。

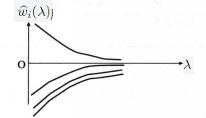
在图4中，和都很不稳定，但其和却大体稳定。这种情况往往发生在自变量和的相关性很大的场合，即在和之间存在多重共线性的情形，从选择自变量的角度，两者只保存一个就够了。这种情况可以解释某些回归系数估计的符号不合理的情形，从实际观点看，和不应有相反符号。

从全局看，岭迹分析可用来估计在某一具体问题中最小二乘估计是否适用，把所有回归系数的岭迹都绘制在一张图上，如果这些曲线比较稳定，如图5所示，利用最小二乘估计会有一定的把握。 

岭迹法缺陷

岭迹法确定k随缺少严格的令人信服的理论依据，存在着一定的主观人为性。

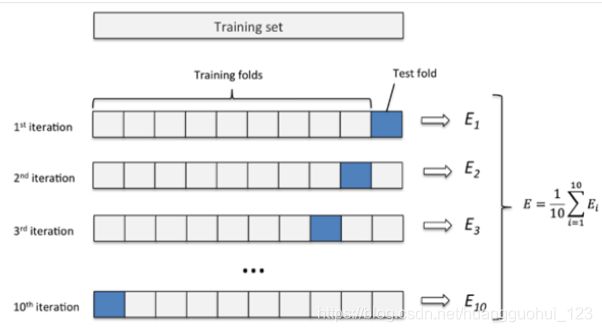
• 交叉验证法

python实现岭回归及岭回归交叉验证 

import numpy as np
from sklearn.linear_model import Ridge,RidgeCV   # Ridge岭回归,RidgeCV带有广义交叉验证的岭回归

#导入数据，切分自变量、因变量
data=np.loadtxt('data5.txt',delimiter='\t')   #读取数据文件
x=data[:,:-1]
y=data[:,-1]


#岭回归(λ=1)
model_ridge=Ridge(alpha=1.0)   #建立岭回归模型对象，需要手动指定岭系数λ值
model_ridge.fit(x,y)
model_ridge.coef_   #自变量的系数
model_ridge.intercept_   #截距

print('_________')

#岭回归_交叉验证
model_ridgecv=RidgeCV() 
model_ridgecv.fit(x,y)
model_ridgecv.coef_   #自变量的系数
model_ridgecv.intercept_   #截距
model_ridgecv.alpha_   #最佳的λ值，只有在使用RidgeCV算法时才有效

输出：

Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, random_state=None, solver='auto', tol=0.001)

array([ 8.50164360e+01, -1.18330186e-03,  9.80792921e-04, -8.54201056e-04,
        2.10489064e-05,  2.20180449e-04, -3.00990875e-06, -9.30084240e-06,
       -2.84498824e-08])

-7443.986528680895

_________

RidgeCV(alphas=array([ 0.1,  1. , 10. ]), cv=None, fit_intercept=True,
        gcv_mode=None, normalize=False, scoring=None, store_cv_values=False)

array([ 8.51015136e+01, -1.17980885e-03,  9.76130177e-04, -8.54548358e-04,
        3.87041364e-05,  2.21156282e-04,  3.15137208e-04,  4.12017107e-06,
        2.59373337e-06])

-7985.757414143803

0.1

 从结果中我们可以看出，当我们指定时，可能并不是最佳的解，通过交叉验证，最佳的解应该是时。

3）LASSO回归（L1正则化）

LASSO是在岭回归的基础上发展的。通过构造一个一阶惩罚函数获得一个精炼的模型，通过最终确定一些指标（变量）的系数为0（岭回归估计系数等于0的机会微乎其微，造成筛选变量困难），解释性很强。LASSO回归和岭回归一样是有偏估计。

LASSO代价函数：

根据拉格朗日乘子法相关概念，可将上式转换为：

,其中为某个阈值。

关于LASS回归下的的求解，这边就不详细介绍了，感兴趣可自行查阅相关资料。

与岭回归的不同在于，此约束条件使用了绝对值的一阶惩罚函数代替了平方和的二阶函数。虽然只是形式稍有不同，但是得到的结果却又很大差别。在LASSO中，当很小的时候，一些系数会随着变为0而岭回归却很难使得某个系数恰好缩减为0. 我们可以通过几何解释看到LASSO与岭回归之间的不同。

同样以两个变量为例，标准线性回归的正则化代价函数还是可以用二维平面的等值线表示，而约束条件则与岭回归的圆不同，LASSO的约束条件可以用方形表示，如下图:

相比圆，方形的顶点更容易与抛物面相交，顶点就意味着对应的很多系数为0，而岭回归中的圆上的任意一点都很容易与抛物面相交很难得到正好等于0的系数。这也就意味着，lasso起到了很好的筛选变量的作用。 

python实现LASSO回归及LASSO回归交叉验证 

import numpy as np
from sklearn.linear_model import Lasso,LassoCV,LassoLarsCV   # Lasso回归,LassoCV交叉验证实现alpha的选取，LassoLarsCV基于最小角回归交叉验证实现alpha的选取


#导入数据，切分自变量、因变量
data=np.loadtxt('data5.txt',delimiter='\t')   #读取数据文件
x=data[:,:-1]
y=data[:,-1]

#lasso回归(λ=1)
model_lasso=Lasso(alpha=1.0)   #建立岭回归模型对象，需要手动指定岭系数λ值
model_lasso.fit(x,y)
model_lasso.coef_   #自变量的系数
model_lasso.intercept_   #截距

print('_________')

#lasso回归_交叉验证
model_lassocv=LassoCV() 
model_lassocv.fit(x,y)
model_lassocv.coef_   #自变量的系数
model_lassocv.intercept_   #截距
model_lassocv.alpha_   #最佳的λ值，只有在使用LassoCV算法时才有效

print('_________')

#基于最小角回归交叉验证实现alpha的选取
model_lassolarscv=LassoLarsCV()
model_lassolarscv.fit(x,y)
model_lassolarscv.coef_   #自变量的系数
model_lassolarscv.intercept_   #截距
model_lassolarscv.alpha_   #最佳的λ值，只有在使用LassoLarsCV算法时才有效

输出：

Lasso(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=1000,
      normalize=False, positive=False, precompute=False, random_state=None,
      selection='cyclic', tol=0.0001, warm_start=False)

array([ 8.39990495e+01, -1.18556429e-03,  1.04475437e-03, -8.53005974e-04,
        2.14916969e-05,  2.14699618e-04, -3.00015988e-06, -9.21929788e-06,
        7.79318985e-08])

-7342.861374586478
_________

LassoCV(alphas=None, copy_X=True, cv=None, eps=0.001, fit_intercept=True,
        max_iter=1000, n_alphas=100, n_jobs=None, normalize=False,
        positive=False, precompute='auto', random_state=None,
        selection='cyclic', tol=0.0001, verbose=False)

array([ 0.00000000e+00, -0.00000000e+00,  3.49200306e-03, -0.00000000e+00,
        1.48547450e-04, -5.47897248e-05, -9.37424204e-07, -1.01533886e-05,
        4.78920457e-07])

1017.6227734339094

20715.847329354765
_________

LassoLarsCV(copy_X=True, cv=None, eps=2.220446049250313e-16, fit_intercept=True,
            max_iter=500, max_n_alphas=1000, n_jobs=None, normalize=True,
            positive=False, precompute='auto', verbose=False)

array([8.36747660e+01, 0.00000000e+00, 2.11454616e-04, 0.00000000e+00,
       0.00000000e+00, 0.00000000e+00, 0.00000000e+00, 0.00000000e+00,
       0.00000000e+00])

-7307.10167123643

0.054387650333886345

 LassoCV和LassoLarsCV都是对Lasso回归的优化。

综述

L2（岭回归）代价函数：

L1（LASSO回归）代价函数：

观测以上的公式，我们可以总结一个通式：

通过控制，我们可以得到不同的公式，以下为为不同值时的惩罚因子的分布：

3、逐步回归法（Stepwise Regression）

逐步回归分析，首先要建立因变量y与自变量x之间的总回归方程，再对总的方程及每—个自变量进行假设检验。当总的方程不显著时，表明该多元回归方程线性关系不成立；而当某—个自变量对y影响不显著时，应该把它剔除，重新建立不包含该因子的多元回归方程。筛选出有显著影响的因子作为自变量，并建立“最优”回归方程。

4、主成分回归（Principal Components Regression）

通过主成分分析，将原始参与建模的变量转换为少数几个主成分，每个主成分是原变量的线性组合，然后基于主成分做回归分析，这样也可以在不丢失重要数据特征的前提下避开共线性问题。

import numpy as np
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression


#导入数据，切分自变量、因变量
data=np.loadtxt('data5.txt',delimiter='\t')   #读取数据文件
x=data[:,:-1]
y=data[:,-1]

#训练pca模型
model_pca=PCA()
data_pca=model_pca.fit_transform(x)
ratio_cs=np.cumsum(model_pca.explained_variance_ratio_)  #主成分方差占比的累积值

rule_index=np.where(ratio_cs>0.8)
index=rule_index[0][0]   #获取第一次大于0.8的索引值
data_pca_result=data_pca[:,:index+1]   #提前主成分

model_linear=LinearRegression()  #建立线性回归模型对象
model_linear.fit(data_pca_result,y)  #输入主成分数据和预测变量y训练模型

model_linear.coef_ #斜率
model_linear.intercept_   #截距

输出：

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

array([1.26262171e-05])

1058.52726

 满足自变量方差大于0.8的主成分为第一个主成分，假设其为，那么方程可以写为：

【注意】

此时的跟岭回归的含义不同：岭回归的是原始数据中的第一个变量，而PCA过后的是第一个主成分——原始数据各个自变量的一个线性组合。

5、手动剔除

直接结合人工经验，对参与回归模型计算的自变量进行删减。