Triangle Attack: A Query-efficient Decision-based Adversarial Attack

Triangle Attack: A Query-efficient Decision-based Adversarial Attack
三角攻击:一种查询高效的基于决策的对抗性攻击

Abstract

基于决策的攻击对实际应用程序构成了严重的威胁，因为它将目标模型视为一个黑箱，只访问硬预测标签。最近已经做出了很大的努力来减少查询的数量;然而，现有的基于决策的攻击仍然需要数千个查询才能生成高质量的对抗示例。在这项工作中，我们发现一个良性样本，当前和下一个对抗样本可以自然地在子空间中为任何迭代攻击构建一个三角形。基于正弦定律，我们提出了一种新的三角形攻击(TA)，利用任何三角形中较长的边总是与较大的角相对的几何信息来优化扰动。然而，直接将这些信息应用于输入图像是无效的，因为它不能彻底探索输入样本在高维空间的邻域。为了解决这个问题，TA优化了低频空间的扰动，由于这种几何性质的普遍性，有效降维。对ImageNet数据集的广泛评估表明，TA在1,000个查询中实现了更高的攻击成功率，并且与现有的基于决策的攻击相比，在各种扰动预算下实现相同的攻击成功率所需的查询数量要少得多。通过如此高的效率，我们进一步验证了TA在现实API，即腾讯云API上的适用性。

1. Introduction

尽管深度神经网络(DNNs)[27,24,25]取得了前所未有的进展，但对抗实例[47]的脆弱性对安全敏感应用构成了严重威胁，例如，人脸识别[42,48,20,30,56,50,15,37,62]，自动驾驶[7,19,4,61,40]等。为了在各种现实应用中安全地部署dnn，有必要对对抗实例的内在特性进行深入分析，这启发了大量对抗攻击[36,6,3,11,8,17,5,52]和防御[34,23,64,57,58,53]的研究。现有的攻击可以分为两类:白盒攻击对目标模型有充分的了解(通常利用梯度)[21,6,34,17]，而黑盒攻击只能访问模型输出，更适用于现实场景。
黑盒攻击可以通过不同的方式实现。基于转移的攻击[32,17,60,55]利用替代模型上生成的对手直接欺骗目标模型。基于分数的攻击[9,26,2,31]假设攻击者可以访问输出日志，而基于决策(又称硬标签)的攻击[5,11,10,29,35]只能访问预测(top-1)标签。
在黑盒攻击中，基于决策的攻击由于攻击所需的信息最少，更具挑战性和实用性。在基于决策的攻击中，对目标模型的查询数量往往起着重要的作用，因为在实践中，对受害者模型的访问通常受到限制。尽管最近的工作设法将查询总数从数百万减少到数千个请求[5,29,38]，但对于大多数实际应用[35]来说，这仍然不够。
现有的基于决策的攻击[5,29,38,35]首先产生一个较大的对抗性扰动，然后通过各种优化方法使扰动最小化，同时保持对抗性特性。
如图1所示，我们发现在第t次迭代时，良性样本x、当前对抗例xadvt和下一个对抗例xadvt+1可以很自然地为任何迭代攻击构建一个三角形。根据正弦定理，在(t +1)次迭代时，对抗例xadvt+1应满足βt+2 αt > π，以保证扰动减小，即δt+1 =∥xadvt+1−x∥p < δt =∥xadvt−x∥p(当βt+2·αt = π时为等腰三角形，即δt+1 = δt)。

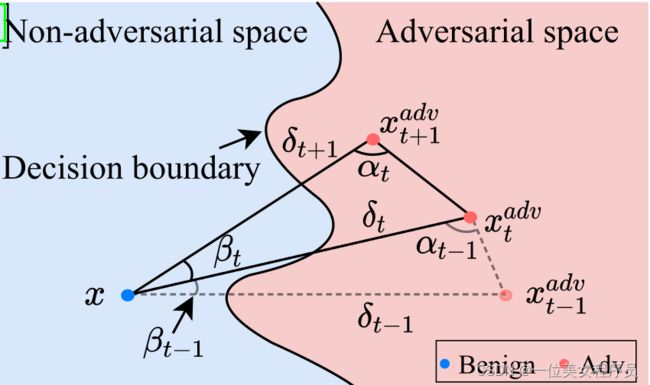
图1:TA任意迭代时的候选三角形示意图。在第t次迭代中，TA在采样子空间中构造一个角αt满足βt + 2αt > π的三角形，寻找一个新的对抗例xadvt+1，并相应地更新αt。注意，与现有的基于决策的攻击不同[5,38,35]，TA没有在决策边界上限制xadvt，而是利用几何特性最小化低频空间中的扰动;使TA本身查询效率高

基于上述几何特性，我们提出了一种新颖且查询效率高的基于决策的攻击，称为三角攻击(Triangle attack, TA)。具体来说，在第th次迭代中，我们随机选择一条穿过良性样本x的方向线来确定一个二维子空间，在这个二维子空间中，我们基于当前对抗例x^adv_t、良性样本x、学习角α_t、搜索角β_t迭代构建三角形，直到构建的三角形的第三个顶点为对抗顶点。利用几何信息，我们可以在离散余弦变换(Discrete cos Transform, DCT)[1]产生的低频空间中进行TA，有效降维，提高效率。并进一步对α_t进行了更新，使其适应于每个构造三角形的扰动优化。与大多数现有的基于决策的攻击不同，它不需要在决策边界上限制x^adv_t，也不需要在每次迭代时估计梯度，从而使TA查询高效。
我们的主要贡献总结如下:

• 据我们所知，这是第一个通过几何信息直接优化频率空间的扰动，而不限制对手在决策边界上，从而获得较高的查询效率的工作。
• 对ImageNet数据集的广泛评估表明，TA在1000个查询中表现出更高的攻击成功率，并且在5个模型上，与现有的SOTA攻击相比，TA只需要更少的查询数量就可以在相同的扰动预算下实现相同的攻击成功率[11,12,8,29,38,35]。
• TA在腾讯云API上生成了更多的对抗性实例，具有难以察觉的扰动，显示了其工业级的适用性。

2. 相关工作

自从Szegedy等人[47]确定了对抗性的例子，大规模的对抗性攻击被提出来愚弄dnn。白盒攻击，如单步梯度攻击[21]、迭代梯度攻击[36,28,34,14]、优化攻击[47,6,3]等，常利用梯度，具有良好的攻击性能。它们已被广泛用于评估防御的模型鲁棒性[34,64,41,13,16]，但由于信息有限，很难在现实世界中应用。为了使对抗性攻击能够应用于实际，各种黑盒攻击，包括基于转移的攻击[17,60,51,52,59]，基于分数的攻击[9,26,49,2,18,63,65]，基于决策的攻击[5,12,8,38,35]，越来越受到人们的关注。其中，基于决策的攻击是最具挑战性的，因为它只能访问预测标签。在这项工作中，我们旨在利用几何信息来提高基于决策的攻击的查询效率，并对现有的基于决策的攻击进行简要概述。
边界攻击[5]是第一个基于决策的攻击，它初始化一个大扰动，并在保持对抗性的情况下在决策边界上执行随机游走。这种范式在随后的基于决策的攻击中被广泛采用。OPT[11]将基于决策的攻击问题定义为具有零阶优化的重值优化问题。而siginpt[12]进一步计算方向导数的符号，而不是快速收敛的幅度。HopSkipJumpAttack (HSJA)[8]通过在决策边界上的二进制信息估计梯度方向来增强边界攻击。QEBA[29]增强了HSJA，使用从不同子空间采样的摄动，包括空间、频率和本征分量，获得更好的梯度估计。为了进一步提高查询效率，qFool[33]假设对例周围的边界曲率较小，并采用多个摄动向量进行有效的梯度估计。BO[43]采用贝叶斯优化在低维子空间中寻找对抗性扰动，并将其映射回原始输入空间，得到最终扰动。GeoDA[38]用超平面近似局部决策边界，并在超平面上搜索与良性样本最近的点作为对手。Surfree[35]在决策边界上迭代构造一个圆，在不进行梯度估计的情况下，采用二叉搜索找到所构造的圆与决策边界的交点作为对手。
现有的大多数基于决策的攻击在决策边界上的每次迭代都限制了对抗实例，并且通常采用不同的梯度估计方法进行攻击。在这项工作中，我们提出了三角攻击，通过利用正弦定律来直接最小化低频空间中的对抗扰动，而不需要梯度估计或将对抗示例限制在决策边界上，从而实现高效的基于决策的攻击。

3. 方法

在本节中，我们首先提供初步的内容。然后我们介绍了我们的动机和提出的三角攻击(TA)。

3.1 准备工作

给定分类器f，参数为θ，良性样本x∈X, 原始标签y∈Y，其中x表示所有图像，y为输出空间。对抗性攻击找到一个对手x^adv∈X来误导目标模型：

其中，ε是扰动预算。基于决策的攻击通常首先产生一个较大的对抗性扰动δ，然后使扰动最小化，如下所示:

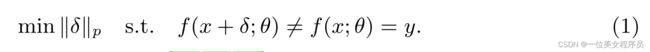
现有的基于决策的攻击[11,12,29]往往估计梯度来最小化扰动，这是耗时的。近年来，一些研究采用几何性质估计梯度或直接优化摄动。这里我们详细介绍了两种几何启发的基于决策的攻击。
GeoDA[38]认为，在数据点x附近的决策边界可以用一个超平面局部逼近，该超平面通过x附近的边界点xB，其法向量为w。因此，式(1)可以局部线性化:

这里x_B是边界上的一个数据点，可以通过多次查询的二分搜索找到，GeoDA随机抽样几个数据点来估计w，以优化每次迭代的扰动。
Surfree[35]假设边界可以用边界点x+δ周围的超平面局部逼近。在每次迭代中，它用极坐标表示对手，并搜索一个最优θ来更新扰动:

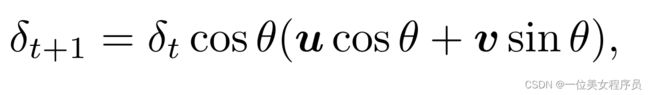
u是从x到x^adv_t的单位向量，v是u的正交向量。

3.2 动机

与大多数基于决策的攻击采用梯度估计[11,12,29,38]或在决策边界上随机游走[5,35]不同，我们的目标是利用几何性质优化摄动，而不对梯度估计进行任何查询。在产生一个较大的对抗性扰动后，基于决策的攻击将对抗性样本移动到良性样本附近，即减少对抗性扰动δ_t，同时在每次迭代中保持对抗性特性。在本研究中，如图1所示，我们发现在第t次迭代时，良性样本x、当前对抗例x^adv_t和下一个对抗例x^adv_t+1可以很自然地在子空间中为任何迭代攻击构造一个三角形。
因此，搜索下一个扰动较小的对敌例x^adv_t+1相当于搜索一个基于x和x^adv_t的三角形，其中第三个数据点x’是对敌的，且满足||x '−x||p <||x^adv_t−x||p。这启发我们利用三角形中角和边长之间的关系来搜索一个合适的三角形，以使每次迭代时的扰动最小化。然而，如第4.4节所示，直接在输入图像上应用这种几何属性会导致非常糟糕的性能。由于这种几何性质的普遍性，我们优化了DCT[1]在低频空间产生的摄动，以实现有效的降维，表现出了如第4.4节所示的巨大攻击效率。
此外，由于Brendel等人[5]提出了边界攻击(BoundaryAttack)，大多数基于决策的攻击[11,12,8,38,35]遵循的设置是每次迭代的对抗示例都应该在决策边界上。我们认为这样的限制在基于决策的攻击中是不必要的，但会在目标模型上引入太多的查询，从而无法接近边界。因此，我们在本研究中不采用此约束，并在第4.4节验证此论证。

3.3 三角攻击

在这项工作中，我们有以下假设，任何深度神经分类器f都存在对抗例子:
假设1：给定一个良性样本x和一个扰动预算ϵ，存在一个对决策边界的对抗扰动∥δ∥_p≤ϵ，该对抗扰动会误导目标分类器f。
这是我们可以找到输入样本x的对抗性例子x^adv的一个一般假设，这已经被许多著作验证过[21,6,3,5,54]。如果这个假设不成立，目标模型是理想的鲁棒性的，因此我们无法在摄动预算内找到任何对抗性的例子，这超出了我们的讨论范围。因此，我们遵循现有的基于决策的攻击框架，首先随机生成一个大型对抗性扰动，然后最小化该扰动。为了与之前的工作保持一致，我们使用二分搜索[29,38,35]在决策边界附近生成一个随机摄动，并主要关注扰动优化。
在任意对敌攻击的扰动优化过程的任意连续两次迭代中，即第t次和第(t+1)次迭代，输入样本x、当前对敌示例x^adv_t和下一个对敌示例x^adv_t+1可以很自然地在输入空间x的子空间中构造一个三角形。因此，如图1所示，减小摄动以生成x^adv_t+1，相当于搜索一个适当的三角形，其中三个顶点分别为x、x^adv_t和x^adv_t+1。
定理1 (sin定理): 假设a, b和c是三角形的边长，α， β和γ是对角，我们有a/sin α = b/sin β = c/sin γ。
由定理1可得图1中三角形的边长与对角的关系:

为了尽量地减小扰动δ_t, 第t个三角形应满足该条件

因此，减小第t次迭代时的扰动可以通过寻找一个由输入样本x、当前对抗样本x^adv_t和角β_t、α_t构成的三角形来实现，该三角形满足β_t+ 2α_t> π且第三顶点为对抗顶点。我们将这样一个三角形表示为候选三角形，将T (x, x^adv_t， α_t， β_t, S_t)表示为第三个顶点，其中St是一个采样子空间。基于此，我们提出了一种新的基于决策的攻击，称为三角形攻击(TA)，在每次迭代中搜索候选三角形并相应地调整角度α_t。
采样频率空间的二维子空间S。输入图像通常位于高维空间中，如ImageNet[27]中的224×224×3，该空间太大，攻击无法有效地探索邻域以最小化对抗扰动。前人的研究[22,29,35]表明，利用不同子空间中的信息可以提高基于决策的攻击效率。例如，QEBA[29]对随机噪声进行采样，在空间变换空间或低频空间中进行梯度估计，但用估计的梯度将输入空间中的扰动最小化。Surfree[35]优化了输入空间子空间中的摄动，该子空间由一个在低频空间中随机采样的单位向量决定。通常，低频空间包含了图像最关键的信息。由于TA在输入空间的性能较差(如第4.4节所示)和几何性质的普遍性(如图2所示)，我们在每次迭代时直接优化频率空间的扰动，以实现有效的降维。我们在低频空间(前10%)中随机抽取一条横过良性样本的d维线。来自良性样本x和当前对手x^adv_t的采样线、方向线可以确定频率空间中唯一的二维子空间S，在该子空间中我们可以构造候选三角形以最小化扰动。通过逆DCT (IDCT)将最终对手转化为输入空间。

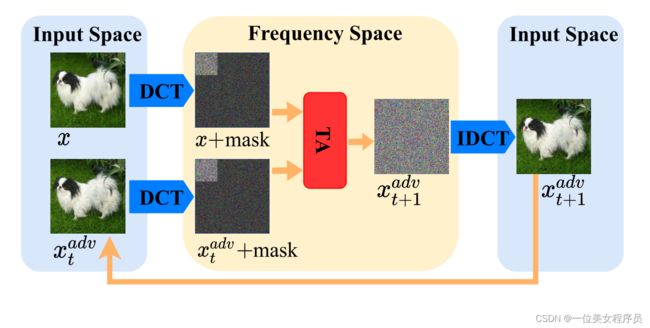
图2:第t次迭代时TA攻击的整个过程示意图。我们在频率空间中构建三角形，以有效地制作对抗示例。注意，这里我们使用DCT来演示，但我们不需要在每次迭代中对x使用它。由于DCT的一对一映射，我们仍然在频率空间中采用x和x^adv_t，没有模糊性

搜索候选三角形。给定子空间S_t，候选三角形只依赖于角β，因为α在优化过程中被更新。如图3所示，如果我们搜索一个角β，而没有找到对敌的例子(x^adv_t+1,1)，我们可以进一步构造一个反方向角度相同的对称三角形，以检验与x^adv_t+1,1具有相同摄动量级但方向不同的数据点x^adv_t+1,2。对于没有歧义的对称三角形，我们将角表示为−β。注意，在相同的角度α下，较大的角度β会使第三个顶点更接近输入样本x，即较小的扰动。确定子空间S_t后，我们首先检查角β_t,0 = max(π−2α， β’)，其中β’ = π/16是一个预先定义的小角。如果T (x, x^adv_t， α_t，β_t,0, S_t)和T (x, x^adv_t， α_t， - β_t,0, S_t)都不是对抗性的，我们放弃这个子空间，因为它不能带来任何好处。另外，我们采用二分搜索的方法，寻找一个使摄动尽可能小的最佳角度β*∈[max(π−2α， β’)， min(π−α， π/2)]。这里我们限制了β的上界，因为T (x, x^adv_t， α_t， β， S_t)将在相反的方向上。X对于β > π/2和π−α保证了一个有效的三角形。

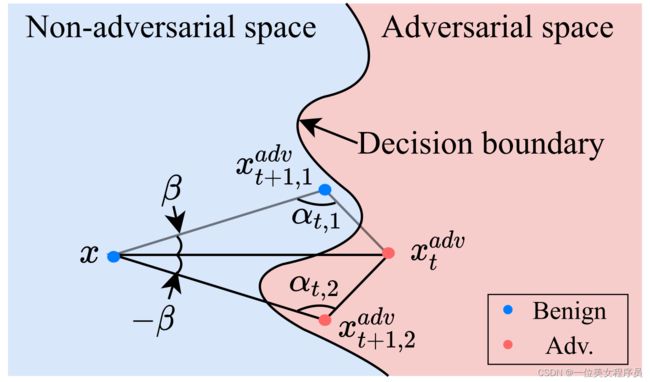
图3:对称候选三角形(x, x^adv_t和x^adv_t+1,2)的说明。当角度β不能导致对抗示例(x^adv_t+1,1)时，我们将进一步基于线= (x, x^adv_t)构建对称三角形，以检查数据点x^adv_t+1,2

调整角度α。直观地说，角度α平衡了扰动的大小和找到对抗性例子的难度:
命题1。在β角相同的情况下，α角越小越容易找到对抗性的例子，而α角越大扰动越小。
直观地看，如图4所示，角α越小，扰动越大，但越有可能越过决策边界，更容易搜索对抗性的例子，反之亦然。每次迭代都很难找到最优α，更不用说各种输入图像和目标模型了。因此，我们根据精心制作的对抗示例自适应调整角度α:

其中x^adv_t,i+1 = T (x, x^adv_t， α_t,i， β_t,i, S_t)为根据α_t,i生成的对抗样例， γ为变化率，λ为常数，τ限制α的上界和下界所产生的对抗性示例。在扰动优化过程中，考虑到失败多于成功，我们采用λ < 1来防止角度下降过快。注意，较大的角度α使它更难找到对抗性的例子。

图4:α的幅值对TA中候选三角形的影响。对于相同的采样角β，角α越大，扰动越小，但越有可能越过决策边界

但是，如果α角过小，β的边界会降低很多，这也使得T (x, x^adv_t， α_t， β_t, S_t)远离当前对抗例x^adv_t，降低了找到对抗例的概率。因此，我们添加α的上界，将其限制在一个适当的范围内。
TA在低频空间采样的子空间St中迭代搜索候选三角形，找到对抗性的例子，并相应地更新角度α。整个TA算法总结在算法1中。