用python 证实poisson过程与指数分布的关系

已知在两次到达间隔直接服从指数分布，请证明在某段固定时间内的到达次数服从Poisson 分布 。

import scipy.stats as st
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm

 


plt.figure()   #exponentail distribution between two arrivals
sample =np.random.exponential(1/5,500)
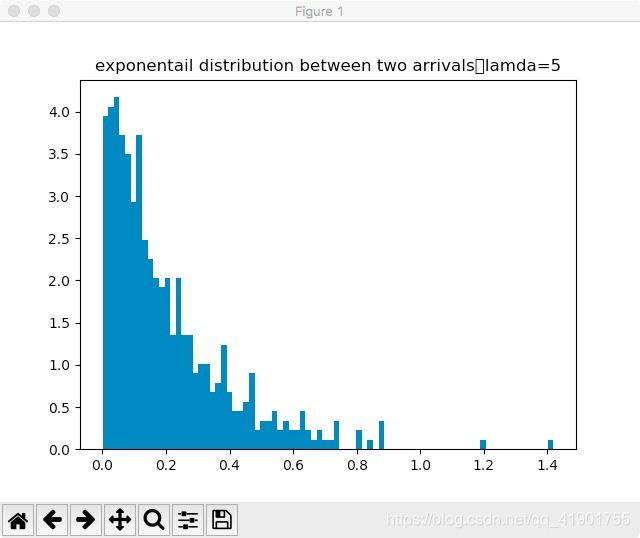
plt.hist(sample, bins=80, normed=True) 
plt.title('exponentail distribution between two arrivals，lamda=5 ZMF_ORIGINAL')
plt.show()



plt.figure()  # generating poisson process according to random exponential distribution 
T=20   # the length of t
arrival_times=np.zeros(1000)
for i in range(0,1000):     # find sample set of 1000 arrival times in T.
    interval_time_sum=np.zeros(501)
    for j in range(0,500):  # stimulate 500 times  arriving  
        interval_time_sum[j+1]= np.random.exponential(1/5) +interval_time_sum[j]    # lamda = 5 
        if interval_time_sum[j+1]>T :
            arrival_times[i]=j
            break
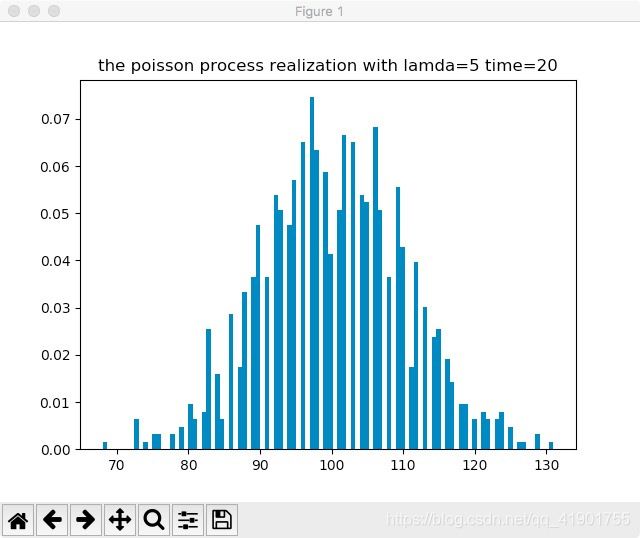
plt.hist(arrival_times, bins=100, normed=True) 
plt.title('the poisson process realization with lamda=5 time=20,ZMF_ORIGINAL')
plt.show()


plt.figure() # a poisson distribution with parameter = 5*20
x = np.random.poisson(lam=5*20, size=1000)
pillar = 200
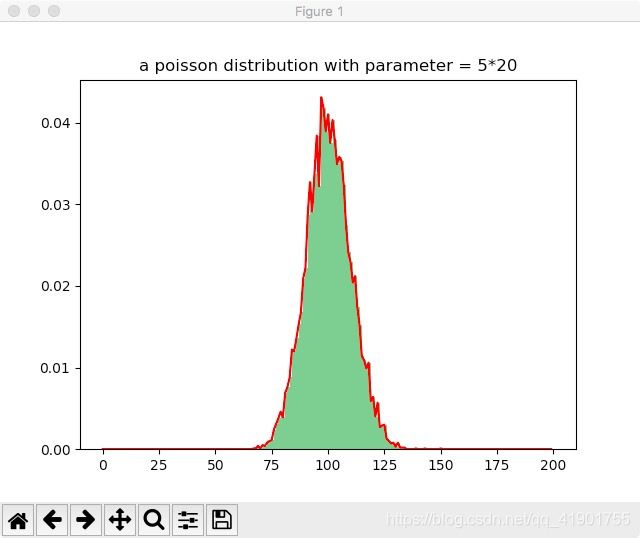
a = plt.hist(x, bins=pillar, normed=True, range=[0, pillar], color='g', alpha=0.5)
plt.plot(a[1][0:pillar], a[0], 'r')
plt.title('a poisson distribution with parameter = 5*20,ZMF_ORIGINAL')
plt.show()

程序解释：
firstly , i upload my programming for your preference, if you find any problems, please let me know and i will appreciate you very much .

my programming code consists of three parts to stimulate the poisson process .

in the first part, i generate the exponential distribution with parameter 5, which represent the probability of interval time between two arrivals .

in the second part, i statistic the probability distribution of arrival times in [0,T] （here, i define T=20） , i am surprised to find that it is really similar to poisson distribution ,which verified our learned knowledge in class !!!

and its mean arrival times is 100, which is actually lamda*T

in the third part, i generate a possion distribution with parameter 5*20 (the same parameter with the second part) to compare them .

运行结果：