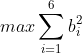基于spss的主成分分析法(Principal Component Analysis,PCA)
主成分分析(Principal Component Analysis,PCA), 将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法。
在实际课题中,为了全面分析问题,往往提出很多与此有关的变量(或因素),因为每个变量都在不同程度上反映这个课题的某些信息。
主成分:由原始指标综合形成的几个新指标。依据主成分所含信息量的大小成为第一主成分,第二主成分等等。
目录
一、前提
数据具有以下特点:
1、维度灾难
2、变量关系不一般
3、主成分与原始变量之间的关系
二、PCA算法步骤
1、模型理论
2、算法步骤
三、用途
四、基于spss的实例操作
结果如下:
1、总方差解释表格:
2、碎石图:
3、成分载荷矩阵:
4、主成分得分矩阵:
5、主成分综合得分排名
参考文献:
一、前提
数据具有以下特点:
1、维度灾难
维度灾难,简单来说就是变量的个数多。如果变量个数增加,随之需要估计的参数个数也在增加,在训练集保持不变的情况下待估参数的方差也会随之增加,导致参数估计质量下降。
2、变量关系不一般
变量关系不一般,指的是变量彼此之间常常存在一定程度的、有时甚至是相当高的相关性,这说明数据是有冗余的,或者说观测数据中的信息是有重叠的,这是我们利用主成分进行降维的前提条件,也可以说这使得变量降维成为可能(观察变量的相关系数矩阵,一般来说相关系数矩阵中多数元素绝对值大于0.5,非常适合做主成分分析,但也不是说小于的就不可以用这种方法)。
在变量个数多,相互的相关性比较大的时候,我们会不会去寻找变量中的“精华”呢?,寻找个数相对较少的综合变量呢?这是我们利用主成分降维的动机。
3、主成分与原始变量之间的关系
(1)主成分保留了原始变量绝大多数信息。
(2)主成分的个数大大少于原始变量的数目。
(3)各个主成分之间互不相关。
(4)每个主成分都是原始变量的线性组合。
针对于此,产生了主成分分析法,主要运用于数据降维。PCA把原先的n个特征用数目更少的m个特征取代,新的m个特征一要保证最大化样本方差,二保证相互独立的。新特征是旧特征的线性组合,提供一个新的框架来解释结果。接下来展开PCA的理论与实践(基于spss):
二、PCA算法步骤
1、模型理论
数据压缩也不是随心所欲地压缩。我们地目标是:让新数据地方差尽可能地大。这样地标准能使得新数据尽可能地不丢失原有数据地信息,因为方差越大,数据间的差异越大。
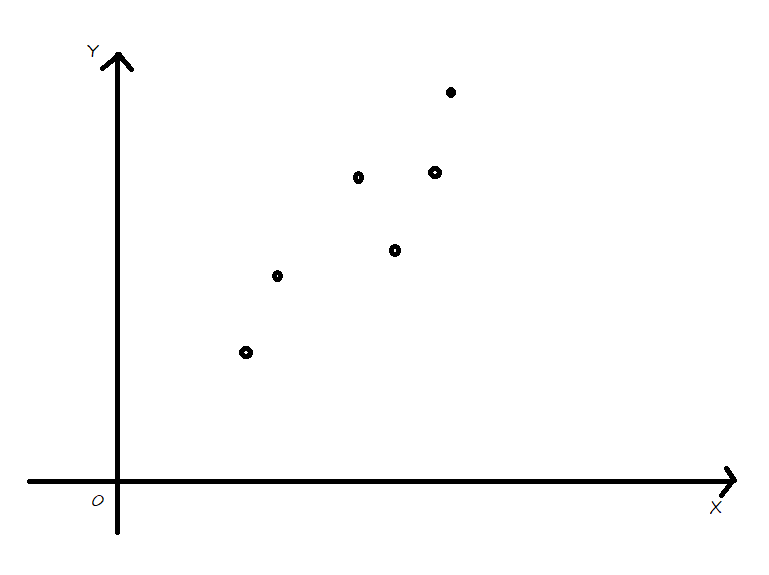
如下图所示:有六个点,每个点有两个特征,分别对应x轴和y轴。我们需要把他们压缩成一维的数据,即每个点只有一个特征。
因此要寻一条直线,让所有点投影到该直线上。该直线上的刻度即为新数据的值。
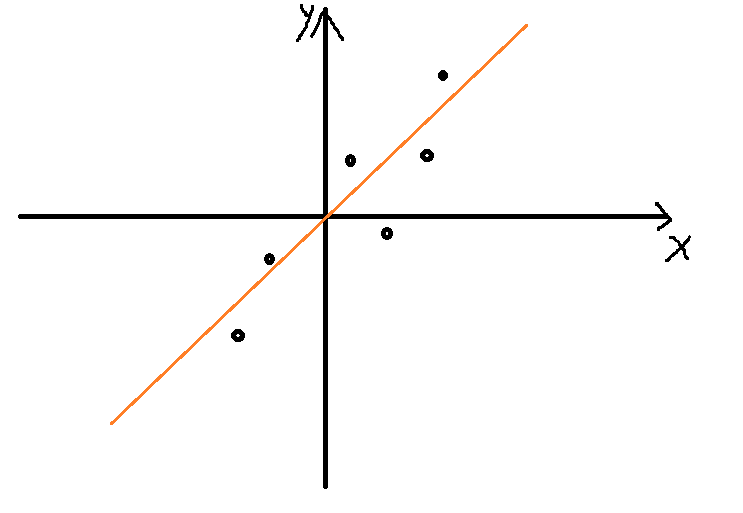
首先我们进行中心化处理。中心化处理的好处在于,我们寻求的直线必定经过原点。如下图所示,我们只需要从所有经过远点的直线中,找一条直线,使得各个数据的方差最大。
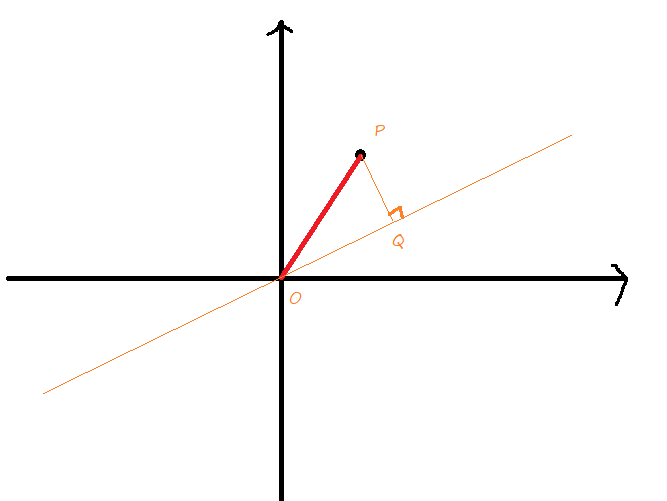
如下图所示,设P是样本的一个数据。注意到这样的一个性质:由于OP的距离是固定的,因此过原点做任何一条直线,记Q是P在该直线上的投影点,都有![]() 。
。
显然,OQ(带正负号的长度)是数据![]() 压缩后的值。
压缩后的值。
那么对于![]() 到
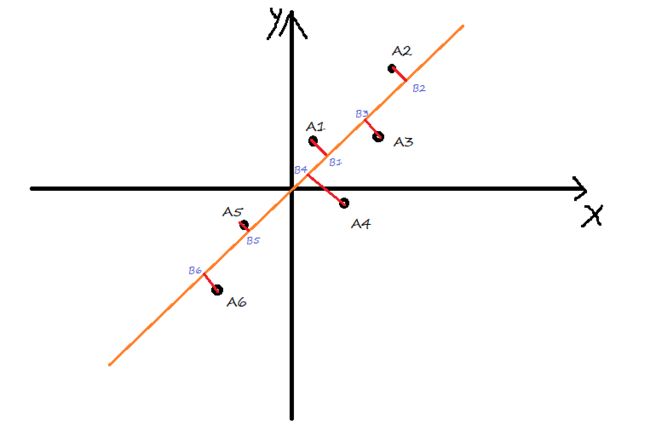
到![]() 六个点,分别做直线的垂线,交直线于
六个点,分别做直线的垂线,交直线于![]() 到
到![]() 六个点。直线可作为数轴,坐标系原点可以看成是数轴的原点。记为
六个点。直线可作为数轴,坐标系原点可以看成是数轴的原点。记为![]() 到
到![]() 六个点的刻度分别为
六个点的刻度分别为![]() 。则
。则![]() 为降维后的数据。
为降维后的数据。
由于数据做了中心化处理后,原点作为了对称轴中心,所以![]() 。
。
记![]() 至直接的距离为
至直接的距离为![]() 。由上述
。由上述![]() 可得:
可得:![]()
2、算法步骤
要解释方差最大和主成分的关系需要从方差和协方差的关系入手:
设有m条n维数据,m个样本,对原始数据标准化(减去对应变量的均值,再除以其方差),每个样本对应p个变量,x=(x∗1,x∗2,⋯,x∗n)′x=(x1∗,x2∗,⋯,xn∗)′。
- 求出自变量的协方差矩阵(或相关系数矩阵);
- 求出协方差矩阵(或相关系数矩阵)的特征值及对应的特征向量;这里是因为主成分分析的解是使原变量达到方差降序排列最大化的正交旋转(证明见张晓庭、方开泰,1982),也就是
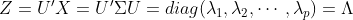
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵aa(为k*p维);
- Y=aT∗XaT∗X (Y 为k*1维)即为降维到k维后的数据,此步算出每个样本的主成分得分
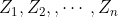 ;
; - 可将每个样本的主成分得分画散点图及聚类,或将主成分得分看成新的因变量,对其做线性回归,聚类分析,分类判别等。(下面实际操作中主要的描述就是争对主成分分析中各成分占比所得综合得分操作)
主成分几何意义是将原由(x1,x2,x3……xp)′构成的原p维RP空间的坐标轴作一正交旋转,一组正交单位向量(t1,t2,⋯,tp)(t1,t2,⋯,tp)表明了p个新坐标轴的方向,这些新的坐标轴彼此仍保持正交,yi是在ti上的投影值,λiλi反映了在t1上投影点的分散程度。
其中,第一主成分和第二主成分要求成分不相关,可考虑到验证它们的特征向量正交,相乘为0;
三、用途
-
主成分评价:在进行包含多个指标的综合评价时,客观且全面是对综合评价结果的必然要求。可惜的是,多个评价指标之间往往存在信息重叠的情况,此外还会存在量纲(计量单位)不统一、权重很难确定等问题。主成分分析方法能够解决以上问题。
-
主成分回归:在线性回归模型中,自变量之间的多重共线性是个让人头痛的问题,它的存在导致拟合出来的线性回归模型结果不尽如人意。这时可以考虑将主成分分析得到的主成分代入到回归模型进行拟合。主成分既保留原来自变量的绝大部分信息,互相之间还是相互对立的,此时再用最小二乘法拟合回归模型,得到的回归系数就能解决“估计不稳定”的缺陷。
例如,通过测试一批年轻体校学员在百米,跳远,跳高,400米,1500米,标枪等10个项目的成绩,将这些成绩进行主成分分析,得到互不相关的几个主成分(公因子),这些主成分可以根据与原项目的相关性,被解释为运动员的耐力,爆发力,弹跳等完全不同的身体核心能力,然后根据这些年轻学员在这些主成分上的得分,专项教练就可以判断这些学员是否适合成为职业运动员以及选择哪个项目作为它们的主项。
四、基于spss的实例操作
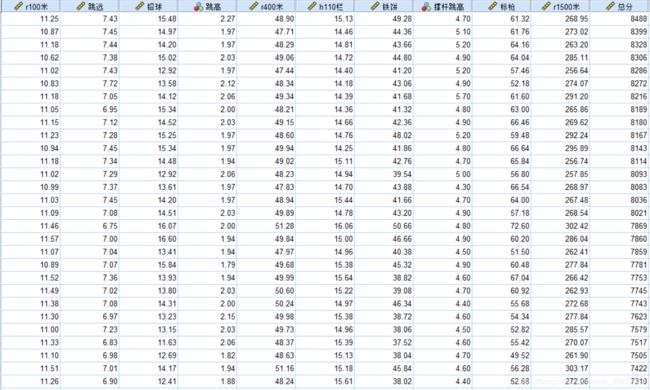
省体工大队打算从一批青年运动员里选择优秀苗子。现在对这批运动员做10个项目的测试,这10个都是田径项目。34个运动员的10个项目的成绩如下。用主成分分析方法对这些运动员的核心能力进行说明。
【分析】-【降维】-【因子分析】-【得分】勾选回归、显示因子得分系数矩阵【提取】勾选碎石图
【描述】勾选相关性矩阵,系数
结果如下:
1、总方差解释表格:
显示提取的主成分的总方差解释量。原来有10的变量(10个运动项目),通过矩阵的正交变换,产生10个新变量,每个新变量能够解释原始数据的方差比例不同,但是所有10个新变量的解释比例之和为100%。在这里,只提取特征值大于1的前两个新变量作为主成分,解释了71.034%的总方差,这个方差贡献率不是很高。当然分析者也可以根据自己的判断点击【提取】按钮选择任意数量新变量作为主成分。
此时主要成分f1,f2就为新变量1、2。
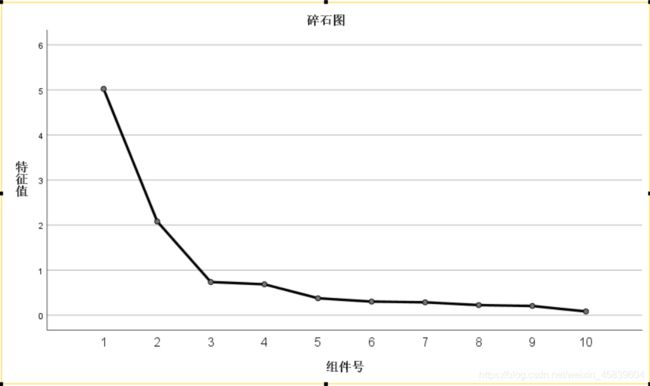
2、碎石图:
可以直观地体现10个新变量的特征值大小(也就是重要程度)
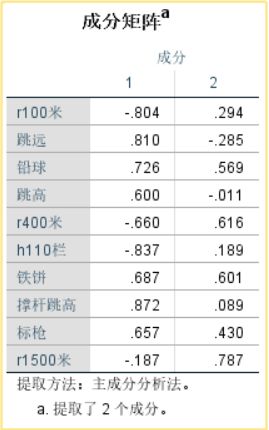
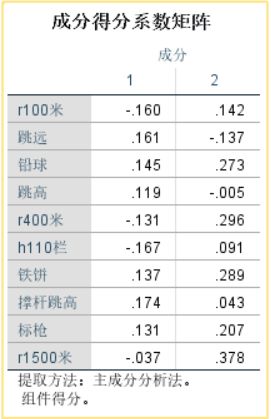
3、成分载荷矩阵:
该矩阵可以说明各主成分在各原始变量上的载荷。
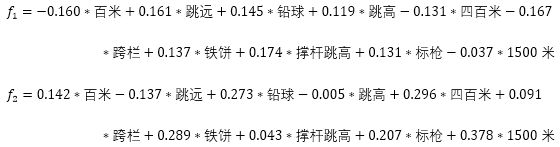
根据载荷矩阵表,可以得到各主成分的表达式:
主成分表达式中的相关系数绝对值越大,表示该主成分对原始变量的代表性越大。可以看出,第一主成分与撑杆跳高的相关系数最大;第二主成分与1500米的相关系数最大。从这个表格中会有一个有趣的发现,第一主成分可以解释为与跳跃和爆发力有关的能力,例如,跳远,跳高,铅球,撑杆跳的相关系数为正,第二主成分可以解释为与跑动和耐力有关的能力,例如四百米,1500米等运动的相关系数较大。
当然这个解释与因子分析相比是模糊的,这也是主成分分析的缺陷所在,例如,100米也需要强大的爆发力。
严格意义上说,不能直接用主成分载荷矩阵写成主成分表达式,而应该用主成分载荷除以主成分特征值的平方根(主成分系数)作为上面式子的回归系数,这是矩阵变换的过程。但是一般情况下,直接用载荷替代系数也是可以的,这不改变主成分的结构和性质。
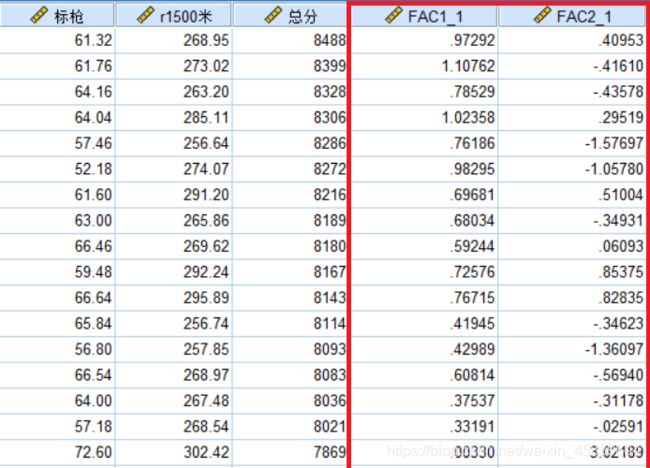
4、主成分得分矩阵:
通过得分矩阵就可以计算每个个案在2个主成分上的得分。这里的得分数值等于上面的载荷数值除以主成分的特征根(-0.160 = -0.804/5.204)。
得分系数矩阵展示的是每个项目在新变量中的得分系数,可以得出下面的得分函数:
只需将每个运动员在各个项目上的运动成绩进行标准化(这里可以使用前面层次分析法的归一化处理),然后代入到得分函数中,就可以得到每个运动员在每个新变量上的得分。
标准化操作:【分析】-【描述统计】-【描述】-勾选【将标准化值另存为变量】
最终得到每个原值进行归一化处理后的Z值:
每个运动员的在每个项目上的得分将会自动计算被保存在新生成的变量FAC1_1和FAC2_1中,如下图所示:
通过每个运动员在两个主成分上的得分,可以大概知道自己是否适合称为职业运动员,以及适合那些类型的项目,是需要速度和爆发力的运动,还是需要耐力的运动。还能分别对这两个得分变量进行降序排列,看看年轻运动员在这两个主成分上的得分排名。
5、主成分综合得分排名
如果想同时考虑两个主成分得分,对运动员进行综合能力的排名,那么就需要考虑两个主成分的权重,计算综合得分的公式为(其中lambda1、2则为上图1中的值):
通过上面的加权计算公式就可以得到每个运动员在这两个主成分上的综合得分,然后再根据综合得分就能获得综合排名。
参考文献:
[1]微信公众号生活统计学:SPSS分析技术:主成分分析;史蒂芬·库里:别看我瘦,我的核心能力强!
[2]泰山教育:主成分分析法
[3]csdn主成分分析:https://blog.csdn.net/qq_42458954/article/details/88786494
[4]百度百科:主成分分析法
[5]知乎用户武辰:关于问题如何通俗易懂地讲解什么是 PCA 主成分分析?的回答