马尔可夫过程
前言
强化学习所研究的是作为主体的智能体与作为客体的环境交互的序贯决策过程。在数学上,我们会将其规范化为一个马尔可夫决策过程(Markov Decision Process,简称为MDP)。由于MDP是强化学习所面对的问题,我们将首先介绍什么是MDP。我们将循序渐进,先介绍马尔可夫性过程,然后介绍MDP,再介绍MDP的不同分类。
马尔可夫过程
在概率论中,随机过程(Random Process)是一门非常重要的学科。学过这门课的同学可能知道,随机过程的严谨定义涉及到概率空间、事件域、流等等数学概念。在这里,我们可以简单地认为,离散时间的随机过程就是按照时间顺序排列好的一系列随机变量 X1,X2,X3,…,Xn,而连续时间的随机过程则可以视为一个含有时间的随机变量 X(T)。我们可以想象,渺小如一个人的心率变化、一台机器的功率周期,宏大到一个国家宏观经济的迭起与兴衰、海平面高度的潮起潮落,背后都有一个连续时间的随机过程。不过,我们为了方便研究,也往往将其简化为一个离散时间的随机过程。随机过程与我们的生产、生活、办公等各方面都是息息相关的。
在数学中,我们研究的是具有某些特殊概率性质的随机过程。我们往往会为假定其背后具有某个概率模型,然后就可以研究其期望、方差等概率性质。例如,我们定义“正态白噪声”为独立同分布的正态随机变量X_t 。大自然中毫无信息的噪声、或是在时间序列测量中产生的误差都可以被视为是“正态白噪声”。当然,“正态白噪声”相当于将一些独立同分布的随机变量串在一起,并没有体现出随机过程的特性,没有太多值得我们研究的地方。一般而言,我们会假定时间序列中X_t之间的因果关系、相关性等概率特性与其在时间上的顺序具有一定的关系。例如,假设时间序列中,当前X_t的取值由之前各个时刻的取值所决定,即时间序列由概率模型 P(X_{t+1} = x | X_t = x_t, X_{t-1} = x_{t-1}, \dots, X_1 = x_1) (在概率论中,我们用大写字母表示随机变量,用小写字母表示具体取值)生成,等等。这样的时间序列才有值得我们研究的地方。
马尔可夫过程(简称为马氏过程)是最经典、也是应用最为广泛的一类随机过程。关于马尔可夫性的严格定义是需要一定现代概率论的基础的,涉及到有关于事件域、流、条件数学期望、自然事件域等数学概念。一般而言,面向工科及应用数学专业的《应用随机过程》中也不会涉及马氏过程的严谨定义,只有在数学专业的《随机过程》中才能找到其严谨定义。在这里,我们不详细赘述马氏过程的严谨定义,而只是介绍其直观的含义:对于一个马氏过程, X_{t+1} 的分布只和 X_t 的取值有关,和 X_t 前面发生过的事情无关。这也就是说, P(X_{t+1} = x | X_t = x_t, X_{t-1} = x_{t-1}, X_{t-2} = x_{t-2}, \dots) = P(X_{t+1} = x | X_t = x_t) 。我们可以想象,初始值是 X 1 X_1 X1是一个随机变量,服从某个初始分布。而 X_1 的取值决定了 X_2 的分布, X_2 的取值又决定了 X_3 的分布,以此类推, X_{n-1} 的取值决定了 X_n 的分布……马氏过程就在这种一环扣一环的因果关系中形成了。
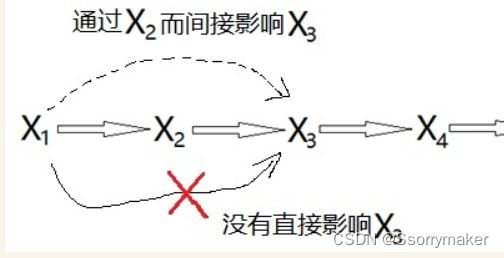
由于我们在定义时没有使用严谨的数学语言,所以难免会产生歧义。我们说 X_3 只是和 X_2 的取值有关,和 X_1 取值无关,这句话是具有歧义的——它并不是真的意味着 X_3 的分布和 X_1 的取值没有关系——明明 X_1 的取值决定了 X_2 ,而 X_2 的取值又决定了 X_3 ,怎么能说 X_3 和 X_1 没有关系呢?
要强调的是,刚才我们所说的“ X_{t+1} 只和 X_t 有关系”这句话,指的是在 X_{t+1} 之前的所有信息( x_1,x_2,\dots,x_t )全部已知的情况下, X_{t+1} 只和 x_t 有关。换句话说,如果我们的手头同时具有 x_1, x_2 的信息,要计算 X_3 的分布,事实上只需用到 x_2 就够了。这是因为 x_1 对于 X_3 的全部影响,都体现在 x_2 之中;但是,如果我们手头没有 x_2 的信息,只有 x_1 的信息,那么这个 x_1 的信息对于我们求解 X_3 无疑也是很重要的。它能给我们带来的信息不如 x_2 这么多,但也绝不是“没有关系”的。在已知 X_1 = x_1 的条件下,我们算出 X_2 的分布 P(X_2=x_2|X_1=x_1) ,再乘以即 X_3 关于 X_2 的条件分布 P(X_3 = x_3 |X_2=x_2) ,即可得到 X_2,X_3 的联合分布 P(X_2=x_2,X_3 = x_3|X_1=x_1) 。然后,可以求出 X_3 的边缘分布 P(X_3 = x_3|X_1=x_1) ,这就等于是利用了 x_1 的取值求出了 X_3 的分布。
上述性质可以加以推广,得到一个马氏链的核心性质:如果我们已知某些条件,去求解某些表达式关于这些条件的期望,则事实上我们只需要那个距离所求事件最接近的条件就够了。例如,求期望表达式 E(X_{16}^2|X_2 = x_2,X_5 = x_5,X_9 = x_9) 时,在三个条件( X_2,X_5,X_9 的取值)之中只需要用到 X_9=x_9 这一个条件就够了。所以,我们有:
E(X_{16}^2 | X_2 = x_2, X_5 = x_5, X_9 = x_9) =E(X_{16}^2 | X_9 = x_9)
另一方面,如果我们有了更加接近 t=15 时刻的信息,比如我们知道了 x_{12} ,那么 X_9=x_9 这条信息自然也用不着了,因为 x_9 对于 E[X_{16}^2] 的所有影响又全部被 x_{12} 的信息给包含在内了。所以,我们又有:
E(X_{16}^2 |X_2 = x_2, X_5 = x_5, X_9 = x_9, X_{12} = x_{12}) = E(X_{16}^2 | X_{12} = x_{12})

如果我们把关于 X_{16} 的函数 X_{16}^2 换为示性函数 I_{X_{16} = x_{16}} ,则我们可以得到上面所说的概率性质:
P(X_{16} =X_{16} | X_2 = x_2, X_5 = x_5, X_9 = x_9) =P(X_{16} = x_{16} | X_9 = x_9)
如果我们把“信息”、“条件”这些概念替换为“自然事件域”、“流”等概念,便可以得到马氏性的严格数学定义。不过在本书中,我们不苛求严谨的定义,只要求读者对马氏性有一个基本的认识:一方面,我们不能误认为 X_3 的分布与 x_1 取值没有关系,而另一方面,我们又可以简单而直接地想象马氏链的产生具有时间上的因果性:从 x_1 产生 x_2 ,从 x_2 产生 x_3 ,以此类推,形成漫长的随机过程。当我们处在这个时间序列上某个位置判断未来走势的时候,只需要用到当前的信息,而不用过去的信息。到底是“有关”还是“无关”,这需要读者自己理清思路。
除了马氏过程之外,人们感兴趣的随机过程还有许多种。例如在二阶自回归模型中,我们设 X_t = aX_{t-1} + bX_{t-2} + \epsilon_t ,其中 A,B 为常系数, \epsilon_t 是一个正态白噪声。在这个过程中,如果我们想估计 X_t ,同时知道 x_{t-1} 与 x_{t-2} 的取值相比仅仅知道 x_{t-1} 无疑是更好的,所以这个时间序列就不具有马氏性。由于马氏过程具有比较好的数学性质以及较成熟的研究成果,所以在实践中人们更加倾向于将问题建模为马氏过程。
打个比方,我们可以用马氏过程来描述某人的一生, X_1 代表他小学的状态, X_2 代表他初中的状态, X_3 代表他高中的状态。如果一个人就读于重点中学,那么他考上985或211的概率也比较大;而如果拥有985的学历,那么取得一份好的工作、走上人生巅峰的概率也比较大。人生就是在这一环紧扣一环的因果中前进的。
对于这个模型,有人可能会有疑问:我以后会经历什么、达到怎样的高度,怎么可能只和现在的我有关、和我小时候发生的事情没有关系?很多童年经历难道不是会影响终生么?如此说来,将现实中某些过程定义为马氏过程是否是不合理的?
这里涉及到一个问题,那就是你定义的“状态”究竟是什么。例如在前面所说的二阶自回归模型中, X_t = aX_{t-1} + bX_{t-2} + \epsilon_t ,则随机变量 X_t 的序列不是一个马氏过程。但是,如果我们设 y_t = (x_t, x_{t-1}) ,则二维随机向量 Y_t 的序列就构成了一个马氏过程。因为我们在估计 Y_t 的分布时,只需要用到 y_{t-1} 的信息。同理,如果我们将一个人的“状态”定义的比较完备,例如,定义一个人现在的状态既包括他的地位、学历,也包括他的性格、见识。那么,他小时候所经历的事情会对他现在的性格与见识产生影响,继而影响未来。只要将“状态”定义得比较完整,使得童年经历对于他的全部影响都已经被其现在的“状态”所包含,那么将人生历程看成马氏过程就显得相对合理了。
从某种意义上来说,一个随机过程能不能用马氏过程来建模,在于我们能不能很好地定义状态以及状态之间的转移方程。对于人生的问题,我们很难定义性格、学识这些状态,也无法判断童年经历会如何影响这种状态。阻碍我们为人生建模的是状态以及转移方程的定义,而非马氏性本身。“马氏性”成立与否主要取决于我们定义的“状态”以及其之间的转移方程是否成立。一旦将随机过程建模为马氏过程,就意味着我们在数学上有更多的手段去研究它。正确理解“马氏性”的含义对我们理解强化学习算法是十分重要的。
