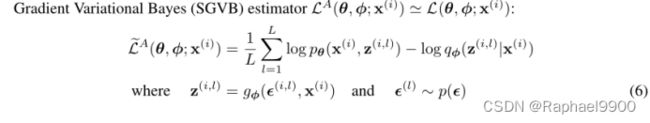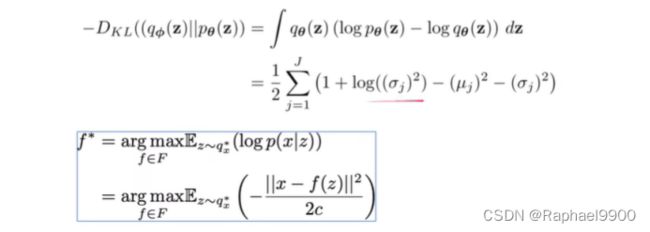Auto Encoding Variational Bayes论文精读

QA：在存在具有棘手后验分布的连续潜在变量和大型数据集的情况下，我们如何在有向概率模型中进行有效的推理和学习?

1、介绍

变分贝叶斯(VB)方法涉及到难以处理的后验逼近的优化。常见的 mean-field approach 需要近似后验期望的解析解，这在一般情况下也是难以处理的。
本文展示了变分下界的重新参数化如何产生一个简单的可微的下界无偏估计量;这个SGVB(随机梯度变分贝叶斯)估计器几乎可以在任何具有连续潜在变量或参数的模型中用于有效的近似后验推理，并且可以直接使用标准随机梯度上升技术进行优化。
本文提出了自动编码VB (AEVB)算法，通过使用SGVB估计器来优化识别模型。使推理和学习特别有效，该模型允许使用简单的先验采样执行非常有效的近似后测推理，这反过来又允许我们有效地学习模型参数，而不需要每个数据点昂贵的迭代推理方案(如MCMC)。当神经网络用于识别模型时，我们得到了variational auto-encoder（VAE）。

2、方法

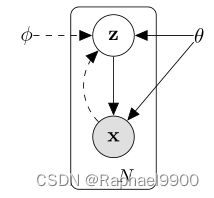
图1:所考虑的有向图形模型的类型。实线表示生成模型pθ(z)pθ(x|z)，虚线表示难解后验pθ(z|x)的变分近似qφ(z|x)。变分参数φ与生成模型参数θ共同学习。
模型联合概率分布可表示为p θ ( x , z ) = p θ ( x ∣ z ) p θ ( z ) ，模型的生成过程为
z ∼ p θ ( z )    ⟹    x ∼ p θ ( x ∣ z ) 。

上面是整个模型的图，我们希望f（z）逼近x。

2.1 问题场景

让我们考虑一个数据集X = {X (i)}Ni=1，由一些连续或离散变量X的N个样本组成。我们假设数据是由一些随机过程生成的，涉及一个未观察到的连续随机变量z。该过程包括两个步骤:
(1)一个值z(i)由某个先验分布pθ∗(z)生成;
(2)值x(i)由某个条件分布pθ∗(x|z)产生。
我们假设先验pθ∗(z)和似然pθ∗(x|z)来自分布pθ(z)和pθ(x|z)的参数族，并且它们的PDFs几乎在θ和z的任何地方都是可微的。真正的参数θ∗以及潜在变量z(i)的值对我们来说是未知的。

我们没有对边际概率或后验概率做常见的简化假设，相反，用一个通用算法，在以下情况下有效:
1、困难:边际似然积分pθ(x) =是很难算的情况(因此我们不能评估或微分边际似然)，其中真实后验密度是难算的(因此EM算法不能使用)，其中任何 reason-able mean-field VB算法所需的积分也是棘手的。这些棘手的问题是相当常见的，出现在中等复杂的似然函数pθ(x|z)的情况下，例如具有非线性隐藏层的神经网络。

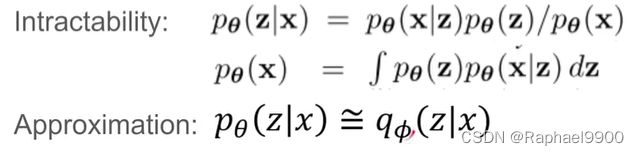
2. 一个大数据集:我们有太多的数据，批量优化成本太高;我们希望使用小批量甚至单数据点进行参数更新。基于采样的解决方案，例如Monte Carlo EM，通常会太慢，因为它涉及到每个数据点典型的昂贵采样循环。

解决方案:
1、参数θ的有效近似ML或MAP估计。
2. 对于参数θ的选择，在给定观测值x的情况下，潜在变量z的有效近似后验推理。
3.变量x的有效近似边际推理。

为了解决上述问题，引入一个识别模型qφ(z|x):一个难以处理的真后验pθ(z|x)的近似值。
从编码理论的角度来看，未观察到的变量z可以解释为潜在的表示或代码。因此，在本文中，我们也将识别模型qφ(z|x)作为概率编码器。因为给定一个数据点x，它会在可能生成数据点x的代码z的可能值上产生一个分布(例如高斯分布)。类似地，我们将pθ(x|z)称为概率解码器，因为给定一个代码z，它会产生x的可能对应值的分布。
本文的思想是，每个样本都有自己特定的正态分布qφ(z∣x)，可以把从特定正态分布采样经过编码器的z还原为x。 我们可从特定分布q(z∣x)中随机采样，生成各式各样与x类似的样本。为了使模型具备通用生成能力，如果所有的q(z∣x)都近似于标准正态分布，就能生成随机样本。
高斯混合模型的生成思想：

2.2变分界

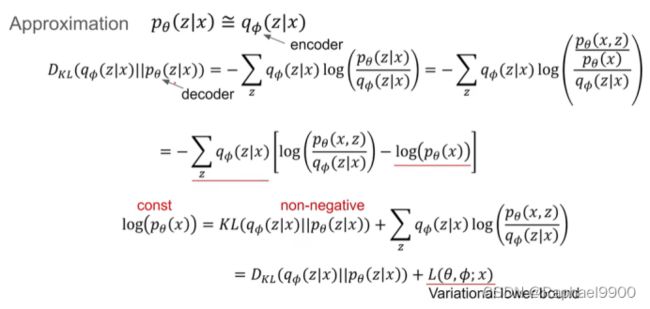
边际似然由单个数据点的边际似然对数的和组成：

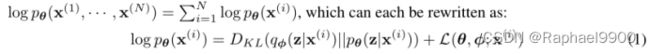
第一个RHS项是真实后验近似的KL散度。由于这个kl散度是非负的，所以第二个RHS项L(θ， φ;X (i))称为数据点i的边际似然的(变分)下界，可以写成

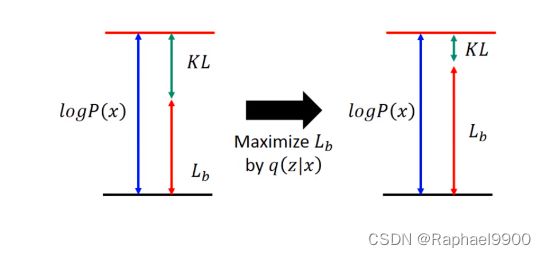
因为KL一定是非负的，所以我们增大下界Lb，可能会增大logP（x）！


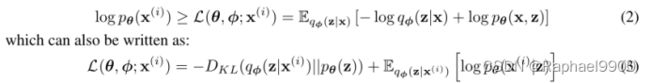
我们假设z和φ是没有关系的，可以得到：

这个梯度估计器显示出非常高的方差，是不切实际的。

2.3 SGVB估计器和AEVB算法

在2.4节中所述的某些温和条件下，对于选择的近似后验qφ(z|x)，我们可以重新参数化随机变量

通过使用可微变换

的辅助噪声变量

引入的这个噪声变量跟z不一样，这个噪声变量是跟z和φ无关的，也就是说z把所有的随机性都转移到了这个变量上，而z就变得可微分了。


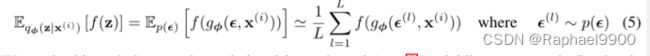
我们将这种技术应用于变分下界(公式(2))，得到我们的SGVB估计量

通常，公式(3)的kl -散度

可以解析积分，使得只有期望重构误差

需要通过抽样进行估计。然后，kl -发散项可以解释为正则化φ，鼓励近似后验值接近先验pθ(z)。这就产生了SGVB估计器。

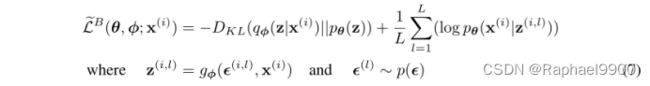
当观察公式(7)中给出的目标函数时，与自动编码器的联系就变得清晰起来。第一项是(近似后测值与先验值的KL散度)作为正则器，而第二项是预期的负重建误差 。函数gφ(.)的选择使得它将数据点x(i)和随机噪声向量e（l）映射到该数据点的近似后验样本:z(i,l) = gφ(e(l)， x(i))。其中z(i,l)∼qφ(z|x(i))。随后，样本z(i,l)被输入到函数log pθ(x(i)|z(i,l))，它等于生成模型（decoder）下给定z(i,l)的数据点时x(i)的概率密度(或质量)。

给定来自数据集X的N个数据点，我们可以基于小批量构建完整数据集的边际似然下界估计器:

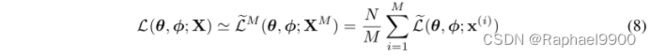
其中，小批量
是从完整数据集x中随机抽取的M个数据点的样本。在我们的实验中，我们发现只要小批量大小M足够大，例如M = 100，每个数据点的样本数量L可以设置为1。导数
，所得到的梯度可以与随机优化方法(如SGD或Adagrad [DHS10])结合使用。

2.4重新参数化技巧

为了解决我们的问题，我们调用了另一种从qφ(z|x)中生成样本的方法。设z为连续随机变量，z ~ qφ(z|x)为某个条件分布。然后，通常可以将随机变量z表示为确定性变量z = gφ(e， x)，e是一个具有独立边缘p(e)的辅助变量，gφ(.)是一个由φ参数化的向量值函数。



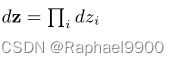
以单变量高斯情况为例:让 z∼p(z|x) = N(µ，σ^2)。在这种情况下，有效的重新参数化是z =µ+ σe，e是辅助噪声变量，e∼N(0,1)。

对于哪个qφ(z|x)我们可以选择这样一个可微变换gφ(.)和辅助变量e∼p (e) ?三个基本方法是:
1.可处理逆CDF。在这种情况下，让e~ U(0, I)，令gφ(e， x)为qφ(z|x)的逆CDF。
2. 类似于高斯分布的例子，对于任何“location-scale”分布族，我们可以选择标准分布(location = 0, scale = 1)作为辅助变量e，让g(.) =location+scale·e。
3.组合:通常可以将随机变量表示为辅助变量的不同转换。
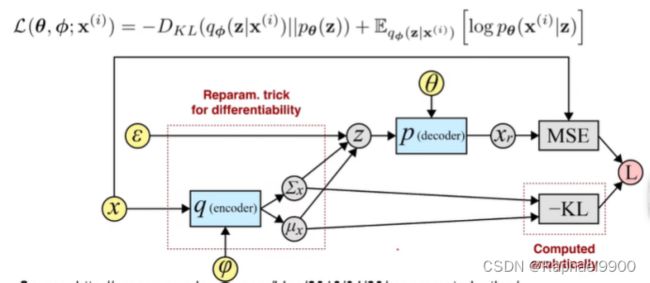
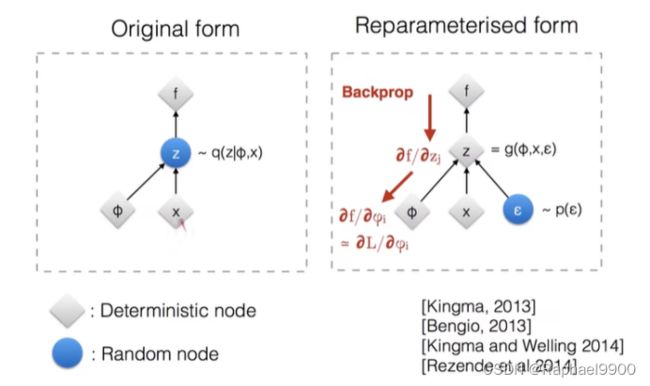
下图对于左边（原形式）是不可以微分z 的，但是右边加入重新参数化技巧之后z就可以微分了。

变分下界(要最大化的目标)包含一个KL项，通常可以分析地积分。在这里，我们给出了当先验pθ(z) = N (0, I)和后验逼近qφ(z|x(I))都是高斯分布时的解。设J为z的维数，设µ和σ表示在数据点i处的变分平均值和s.d.，设µJ和σ J简单地表示这些向量的第J个元素。
高斯MLP作为编码器或解码器：在这种情况下，让编码器或解码器是一个具有对角协方差结构的多元高斯:

其中{W3, W4, W5, b3, b4, b5}是MLP作为解码器时的权值和偏置以及θ的一部分。注意，当这个网络被用作编码器qφ(z|x)时，则z和x交换，权重和偏差为变分参数φ。



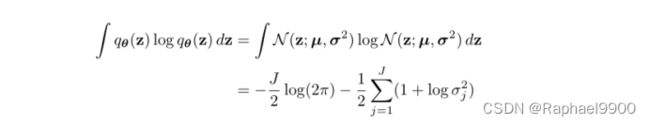
计算如下：

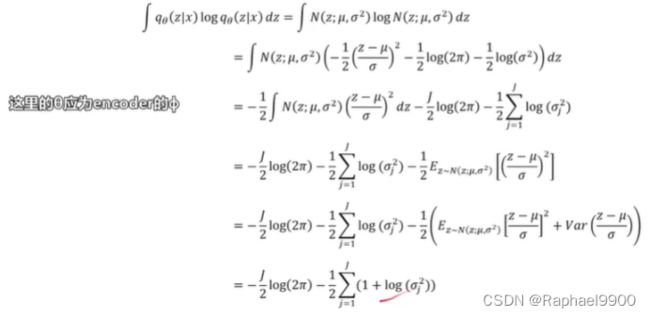
3、举例:变分自动编码器VAE

将神经网络用于概率编码器qφ(z|x)(生成模型pθ(x, z)的后验逼近)，其中参数φ和θ与AEVB算法一起优化。

可以让变分近似后验是一个具有对角协方差结构的多元高斯分布:

其中，近似后验的均值和方差（µ(i)和σ(i)）是编码MLP的输出，即数据点x(i)的非线性函数和变分参数φ。

我们从后验z(i,l)∼qφ(z|x(i))取样，使用z(i,l) = gφ(x(i)， e(l)) =µ(i) + σ(i)点积e ，e(l) ~ N (0, I)，用e我们表示一个元素乘积。该模型和数据点x(i)的结果估计量为:

4、相关工作

清醒-睡眠算法是文献中唯一适用于同一类连续潜变量模型的在线学习方法。清醒-睡眠算法采用了一个接近真实后验的识别模型。清醒-睡眠算法的一个缺点是，它需要同时优化两个目标函数，这两个目标函数一起不对应于边际似然(一个界)的优化。清醒-睡眠的一个优点是它也适用于具有离散潜在变量的模型。每个数据点的Wake-Sleep计算复杂度与AEVB相同。

AEVB算法暴露了有向概率模型(用变分目标训练)和自动编码器之间的联系。线性自动编码器和某一类生成线性-高斯模型之间的联系早已为人所知。在[Row98]中，证明了PCA对应于线性-高斯模型的一种特殊情况下的极大似然(ML)解，该模型具有先验p(z) = N (0, I)和条件分布p(x|z) = N (x;Wz，∈I)，特别是有无穷小∈的情况。

5、实验

本文训练了来自MNIST和Frey Face数据集的图像生成模型3，并在变分下界和估计的边际似然方面比较了学习算法。参数更新使用随机梯度上升，其中梯度是通过微分下界估计量∇θ，φ L(θ， φ;X)(见算法1)，加上一个小的权值衰减项，对应于先验p(θ) = N (0, I)。

本文将AEVB的性能与清醒-睡眠算法[HDFN95]进行了比较。VAE在清醒-睡眠算法和变分自编码器中使用了相同的编码器(也称为识别模型)。所有参数(包括变分参数和生成参数)均从N(0,0.01)中随机抽样初始化，并采用MAP准则进行联合随机优化。步长采用Adagrad [DHS10];Adagrad全局步长参数根据前几次迭代中训练集的性能从{0.01,0.02,0.1}中选择。使用M = 100的小批，每个数据点L = 1个样品。

Likelihood lower bound似然下界 我们训练了生成模型(解码器)和相应的编码器(也就是识别模型)，在MNIST的情况下有500个隐藏单元，在Frey Face数据集的情况下有200个隐藏单元(为了防止过拟合，因为它是一个相当小的数据集)。所选择的隐藏单元数量是基于先前关于自动编码器的文献，不同算法的相对性能对这些选择不是很敏感。图2显示了比较下界时的结果。有趣的是，多余的潜变量并不会导致过拟合，这可以用变分界的正则性来解释。

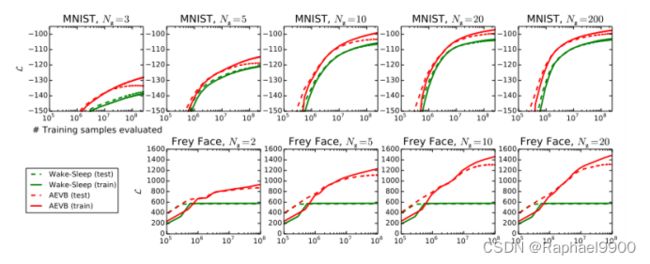
图2:对于不同维数的潜在空间(Nz)，AEVB方法与清醒-睡眠算法在优化下界方面的比较。AEVB方法收敛速度快得多，在所有实验中都得到了更好的解。

Marginal likelihood边际似然 对于非常低维的潜在空间，可以使用MCMC估计器估计学习生成模型的边际似然。对于编码器和解码器，我们再次使用神经网络，这次有100个隐藏单元和3个潜在变量;对于高维潜在空间，估计变得不可靠。同样，使用了MNIST数据集。采用混合蒙特卡罗(HMC) [DKPR87]采样器，将AEVB和清醒-睡眠方法与蒙特卡罗EM (MCEM)进行比较。我们比较了这三种算法的收敛速度，对于小的和大的训练集大小。结果如图3所示。

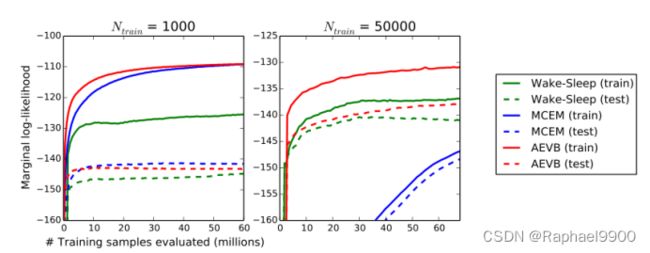
图3:对于不同数量的训练点，AEVB与清醒-睡眠算法和蒙特卡洛EM在估计边际似然方面的比较。蒙特卡洛EM不是一种在线算法，并且(与AEVB和清醒-睡眠方法不同)不能有效地应用于完整的MNIST数据集。

高维数据的可视化 如果我们选择一个低维潜在空间(例如D)，我们可以使用学习的编码器(识别模型)将高维数据投射到低维流形。