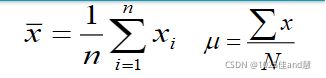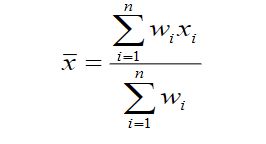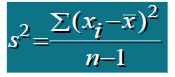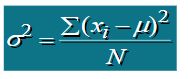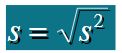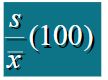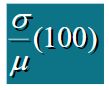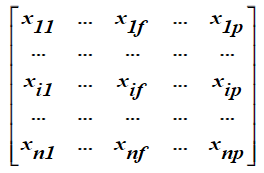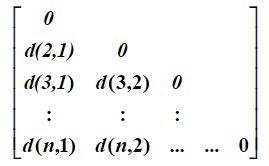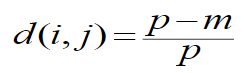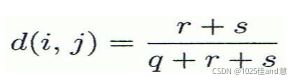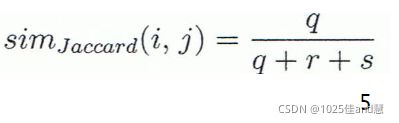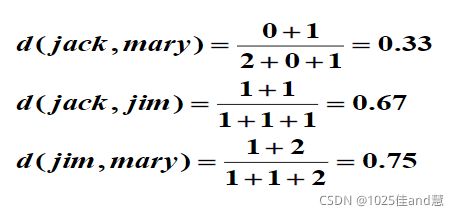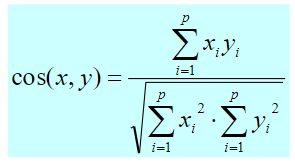数据挖掘（python实现）—认识数据

1.数据对象与属性类型

数据集合的类型：记录、图或网络、有序的列表、空间、图像和多媒体等。

数据集由数据对象构成，一个数据对象代表一个实体。又称为样本，事例，数据点，对象，元组等。

数据对象由属性来描述。

属性（也称作维度，特征，变量）：一个数据字段表示一个数据对象的某个特征。

属性类型：标称属性——与名称有关

                        类别、状态等

                        Hair_color={auburn,black,blond,brown,grey,red,white}

                        婚宴状态，职业，ID号，邮政编码

                  二元属性——是一种特殊的标称属性或布尔属性

                        只有2个状态的名词性属性（0和1）

                        对称二元：同样重要，例如性别

                        非对称：非同等重要，例如医疗检查中的阴性和阳性

                  序数属性——有意义的序，但是相继值之差是未知的

                        值有一个有意义的排序，但连续值之间的大小未知，例如衣服大小号                       

                        Size={small，medium，large}，等级等 

                  数字属性——数量的

                        区间标度：相等的单位尺度，没有真正的零点，如年;

                        比率标度：具有固定零点的数值属性，如重量，身高等。 

标称属性、二元属性和序数属性都是定性的。

离散属性和连续属性：

离散属性——一个有限的或可数无限集值，例如邮政编码

连续属性——属性值为实数，通常表示为浮点变量

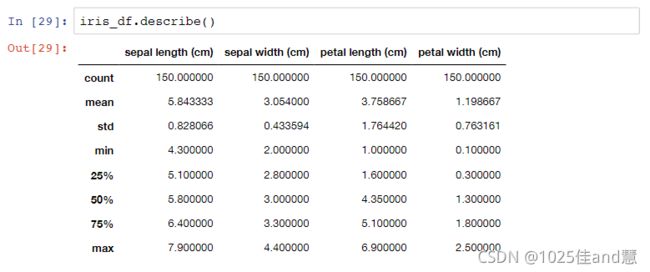
2.数据的基本统计描述

（1）数据描述性统计之集中趋势—均值，中位数，众数

均值（样本vs总体）（mean）：n是样本大小，N是总体大小

         加权算术均值：

         截断均值：去掉高低极端值

中位数（median）：奇数则为有序集的中间值，否则为中间两个数的平均

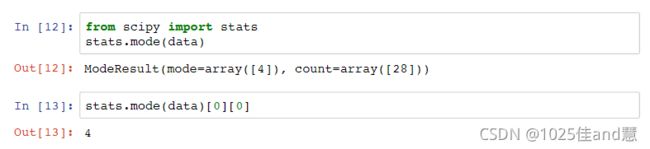
众数（Mode）：出现频率最高的值，经验公式mean-mode=3×(mean-median) 

（2）描述性统计之离散趋势—变异程度的度量

极差（全矩）：

        极差（range，全距）是数据中最大与最小间的差距

        是衡量数据变异程度最简单的描述

        全距对最大与最小数据的值的敏感性很强

分位数（分位点，percentile）：

        将一个随机变量的概率分布范围分为几个等份的数值点

        常用中位数（二分位数）、四分位数、百分位数等

四分位数（quartile）：Q1,Q2,Q3,Q4

中间四分位数极差（Inter-quartile range）：IQR=Q3-Q1

        四分位点内距是第三与第一四分位数间的差距

        是中间50%的数据的全距

        它能够克服极端值的影响

五数概况（five-number summary）：最小值，Q1，中位数，Q3，最大值

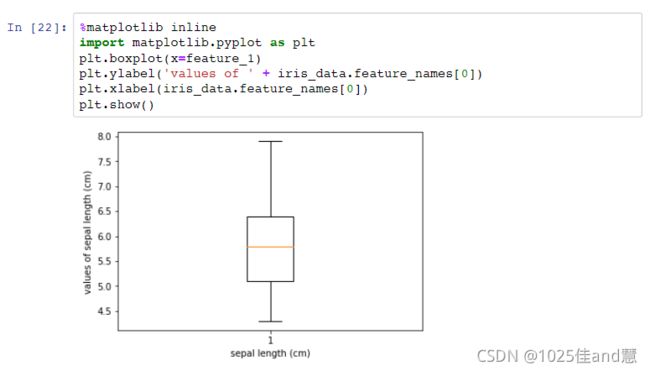
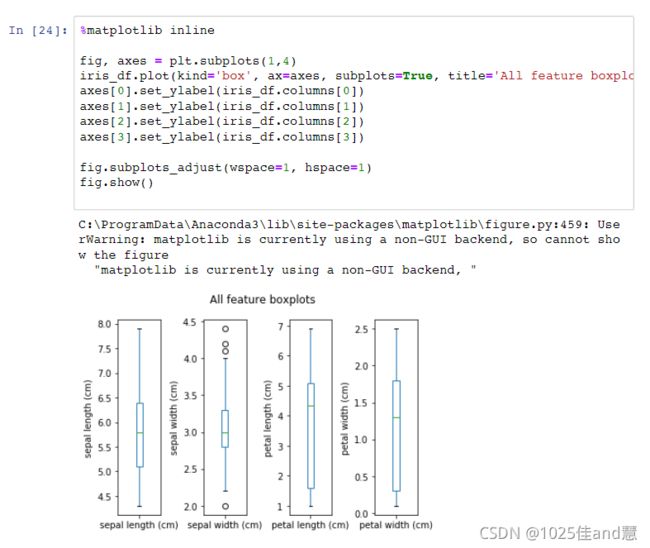
Boxplot:

        使用盒子表示数据

        盒子两端是第1/3四分位数，即盒子高度为四分位数极差IQR

        盒内的线表示中位数

        胡须：不超过四分位数1.5×IQR的最大/小数据点

        离群点（Qutliers）：单独绘出满足某个离群点阈条件的离群点

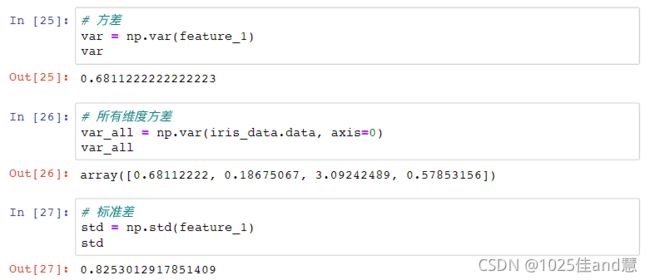
方差：方差是各数据值与平均值之间的差异

         如果数据集为样本，样本方差为

         如果数据集为总体，总体方差为 

 标准差：标准差为方差的正平方根

         如果数据集是样本，样本标准差为

         如果数据集为总体，总体标准差为 

变异系数：变异系数是标准差相对于平均数的大小的度量。

         如果数据集为样本，计算为 

         如果数据集为总体，计算为 

（3）描述性统计分析—离散趋势度量

 极差（range），四分位数（Quartiles），离群点（outliers），盒图（boxplots）

        极差（range）：max-min

        四分位数（quartile）：Q1（25百分位数percentile），Q3（75百分位数percentile）

        中间四分位数极差（Inter-quartile range）：IQR=Q3-Q1

        五数概括：min,Q1,median,Q3,max

        盒图：盒两端为四分位数，中位数标记，添加胡须，离群点独立标出

        离群点：通常是值高/低于四分位数1.5×IQR

方差/标准差（样本；总体）

        方差（Variance）：

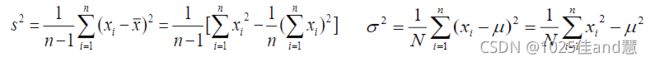标准差（Standard deviation）：方差的平方根

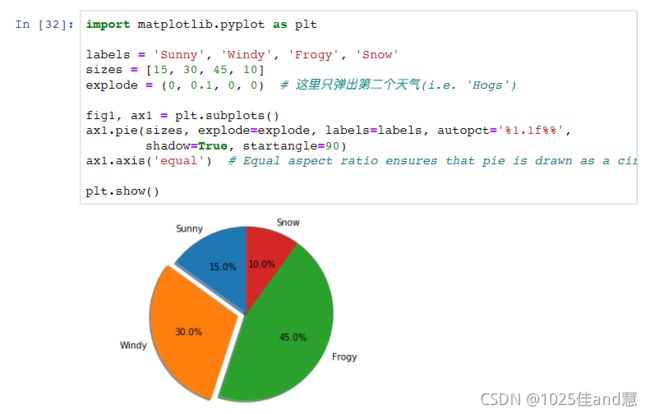
（4）描述性统计之基本统计图形

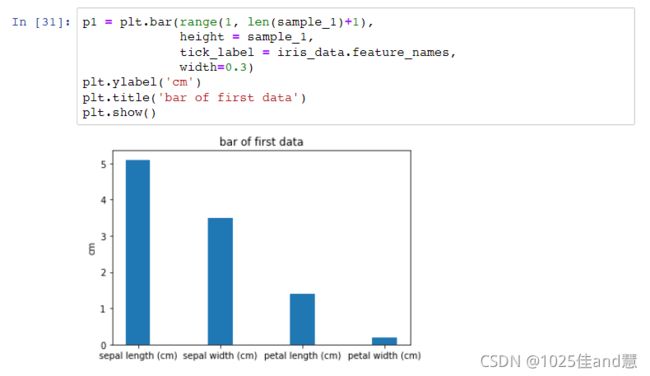
直方图（Histogram）：图形显示每个列值的频率，条形图所示

        显示有多大比例的点下落入每个类别

        类别并不是均匀的宽度时有别于条形图一个关键：条形图的面积表示值而不是条形图的高度

        类别通常指定为变量的一些非重叠区间。类别必须相邻

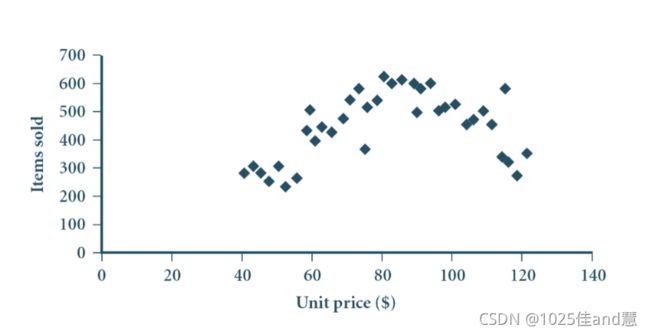
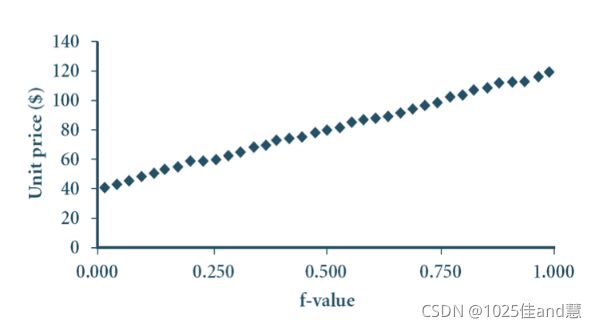
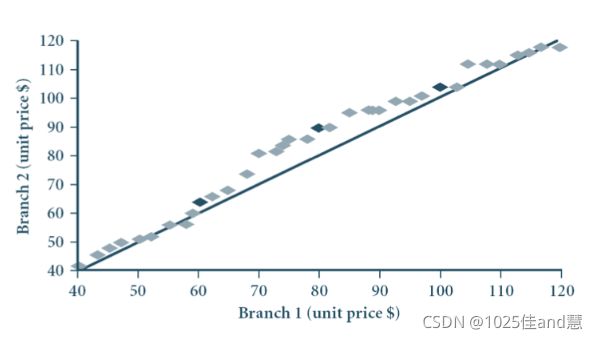
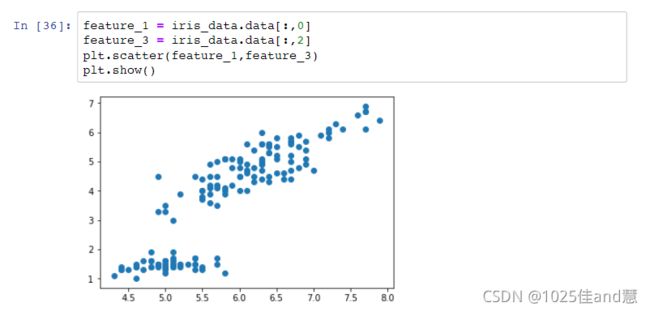
散点图（Scatter plot）：

        提供双变量的数据的第一印象：点的聚集，离群点等

        每个值对作为一个坐标点绘于平面上

        

分位数图（Quantile Plot）： 

        显示所有数据（允许用户评估全部行为和不寻常的事件）

       

 分位数-分位数图（Q-Q图）：

        对着另一个分位数，绘制一个单变量分布的分位数

        

 3.数据的相似性和相异性度量

（1）数据的相似性和相异性度量

 相似性（Similarity）：

        数值测量两个数据对象类似程度

        目标越相似时值越大

        通常介于[0,1]

相异性（Dissimilarity）：

        数值测量两个数据对象差异程度

邻近度（Proximity）

（2）数据矩阵和相异度矩阵

数据矩阵（Data matrix）：

相异性矩阵（Dissimilarity matrix）： 

 （3）标称属性（名词性）的邻近度量

2个或多个状态，例如：red,yellow,blue,green（二元属性的推广）

方法1：简单匹配：

        m：p个变量中匹配的个数

        p：全部变量的个数

        

方法2：使用一系列的二进制属性

        为M个名义状态的每一个产生一个新的二进制/二元属性

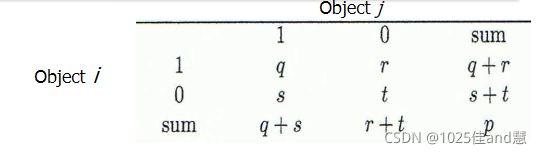
二进制数据的列联表：

         

 对称二元变量的距离侧度：

        

不对称二元变量的距离侧度 ：

        

Jaccard系数（不对称二元变量的相似性侧度）：

         

 二进制属性的相异度量

        性别是对称属性

        其他属性是非对称属性

        令 Y和 P值为1，且N值为0

                

 （4）数值属性相异性测度

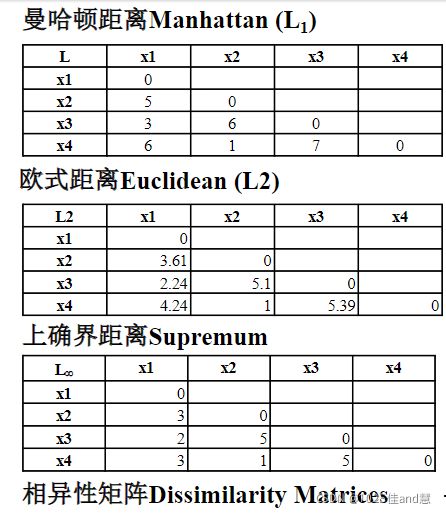
Minkowski distance：一种流行的距离测度

 h=1：曼哈顿距离（L1范数）

        

h=2：欧氏距离

         

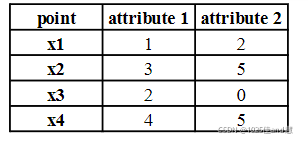
 计算例子：

 

 （5）数值属性相异性测度—标准化

Z-score：

        x：需标准化的原始数值，u：总体均值，σ：标准差

        在标准偏差单位下，原始分数和总体均值之间的距离：“-”，“+”

        数值属性相异性计算之前，一般先进行数据标准化处理

 （5）余弦相似性

文档用词频来进行量化和表上，如下

余弦相似性计算公式： 

         

 

 4.python操作实现

数据的基本统计描述—集中趋势

 

 均值

中位数

 众数

方法一：

 方法二：

数据的基本统计描述—离散趋势

 

极差

 四分位数

 四分位数极差（四分位距）

五数概况

单一箱线图

 多个箱线图

 方差和标准差

 DataFrame描述性统计

数据的基本统计描述—基本统计图

条形图

饼状图

 折线图

直方图

 散点图

分位数—分位数图

雷达图 

词云

 计算数值属性的三种距离