【Matlab】复化梯形公式求积分、求二重积分
目录
- 一、复化梯形公式求积分
-
- 1.1 题目
- 1.2 程序
- 1.3 运行结果
- 二、复化梯形公式求二重积分
-
- 2.1 题目
- 2.2 程序
-
- 2.2.1 二重积分通用程序
- 2.2.2 主函数程序
- 2.3 运行结果
一、复化梯形公式求积分
1.1 题目
利用复化梯形公式计算
I ( f ) = ∫ 1 5 s i n x x d x I(f) = \int_1^5{\frac{sinx}{x}dx} I(f)=∫15xsinxdx
的近似值,精确至7位有效数字。
1.2 程序
clc; clear all
syms x
%% 已知条件
Fx(x) = sin(x)/x;
a = 1;
b = 5;
epsilon = 5e-8;
e = 1;
T = []; % 存放Tf的值
h = b-a;
Xk1 = [a, b]; % 存放已选的 xk
Xk2 = []; % 存放将要使用的 x(k+1/2)
sumfx = 0; % sum( fx(k+1/2) )
%% 计算
digits(8)
format long
k = 0;
Tf = vpa( b - a ) / 2 * ( Fx(a) + Fx(b) );
T = [T, Tf];
fprintf('k=%d, 2^k=%d, Tk=%0.8f\n',k,2^k,Tf)
while(e>epsilon)
for i=1:length(Xk1)-1
temp = ( Xk1(i) + Xk1(i+1) ) / 2;
sumfx = sumfx + Fx(temp);
Xk2 = [Xk2,temp];
end
Xk1 = [Xk1,Xk2];
Xk1 = sort(Xk1);
k = k + 1;
Tf = vpa( 0.5 * ( Tf + h * sumfx ) );
T = [T, Tf];
e = abs(Tf - T(end-1))/3;
fprintf('k=%d, 2^k=%d, Tk=%0.8f, e=%0.8f\n',k,2^k,Tf,e)
% 更新值
h = h / 2;
sumfx = 0;
Xk2 = [];
end
If = Tf;
fprintf('复化梯形求积公式的结果为:%0.8f\n',If)
1.3 运行结果
二、复化梯形公式求二重积分
2.1 题目
(1)给定积分 I ( f ) = ∫ c d ( ∫ a b f ( x , y ) d x ) d y I(f)=\int_{c}^{d}\left(\int_{a}^{b} f(x, y) \mathrm{d} x\right) \mathrm{d} y I(f)=∫cd(∫abf(x,y)dx)dy,取初始步长 h h h和 k k k及精度 ε \varepsilon ε,应用复化梯形公式,采用逐次二分步长的方法并应用外推思想编制计算 I ( f ) I(f) I(f)的通用程序,计算至相邻两次近视值之差的绝对值不超过 ε \varepsilon ε为止;
(2)用所编程序计算积分 I ( f ) = ∫ 0 π / 6 ( ∫ 0 π / 3 tan ( x 2 + y 2 ) d x ) d y I(f)=\int_{0}^{\pi / 6}\left(\int_{0}^{\pi / 3} \tan \left(x^{2}+y^{2}\right) \mathrm{d} x\right) \mathrm{d} y I(f)=∫0π/6(∫0π/3tan(x2+y2)dx)dy
取 ε = 1 2 × 1 0 − 5 \varepsilon=\frac{1}{2} \times 10^{-5} ε=21×10−5。
2.2 程序
2.2.1 二重积分通用程序
function[result] = trapezoid(a,b,c,d,F,epsilon)
%% 初值条件
T0 = []; % 存放Tm,n(f)
T1 = []; % 存放T(1)m,n(f)
T2 = []; % 存放T(2)m,n(f)
T3 = []; % 存放T(3)m,n(f)
m = 1; % 将[a,b] m等分
n = 1; % 将[c,d] n等分; 注:虽然这里m与n相等,但分开计算。
h = (b - a) / m; % x的步长
k = (d - c) / n; % y的步长
xx = [a,b];
yy = [c,d];
e = 1; % 误差
%% 计数位
count = 0;
T0_count = 0;
T1_count = 0;
T2_count = 0;
T3_count = 0;
%% 计算
digits(10)
T = h * k / 4 * ( F(xx(1),yy(1)) + F(xx(1),yy(2)) + F(xx(2),yy(1)) + F(xx(2),yy(2)) ) ;
T0 = [T0, T];
T0_count = T0_count + 1;
count = 1;
fprintf('k=%d, 2^k=%d, T0=%0.8f\n',count,2^count,T)
while(e>epsilon)
m = 2 * m;
n = 2 * n;
h = (b - a) / m;
k = (d - c) / n;
% 计算x、y的取值
xx = [a]; % 暂时只存入左边值
yy = [c]; % 暂时只存入左边值
for i = 1:m
temp = a + i * h;
xx = [xx,temp];
end
for j = 1:n
temp = c + j * k;
yy = [yy,temp];
end
% 计算T0
T = 0;
for i = 1:m
for j = 1:n
T = T + vpa( h * k /4 * (F(xx(i),yy(j)) + F(xx(i),yy(j+1)) + F(xx(i+1),yy(j)) + F(xx(i+1),yy(j+1)) ) );
end
end
T0 = [T0,T];
T0_count = T0_count + 1;
count = count + 1;
fprintf('k=%d, 2^k=%d, T0=%0.8f',count,2^count,T)
% 计算T1
if T0_count - T1_count == 2 && T0_count >= 2
temp = 4 / 3 * T0(end) - 1 / 3 * T0(end-1);
T1 = [T1,temp];
T1_count = T1_count + 1;
fprintf(', T1=%0.8f',T1(end))
end
% 计算T2
if T1_count - T2_count == 2 && T1_count >= 2
temp = 4 / 3 * T1(end) - 1 / 3 * T1(end-1);
T2 = [T2,temp];
T2_count = T2_count + 1;
fprintf(', T2=%0.8f',T2(end))
end
% 计算T3
if T2_count - T3_count == 2 && T2_count >= 2
temp = 4 / 3 * T2(end) - 1 / 3 * T2(end-1);
T3 = [T3,temp];
T3_count = T3_count + 1;
fprintf(', T3=%0.8f',T3(end))
end
if T3_count >= 2
e = T3(end) - T3(end-1);
fprintf(', e=%0.8f',e)
end
fprintf('\n')
end
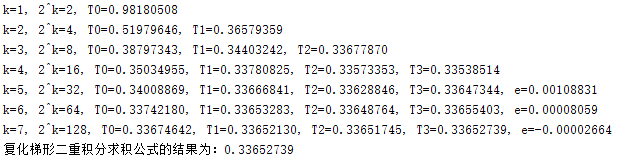
fprintf('复化梯形二重积分求积公式的结果为:%0.8f\n',T3(end))
result = T3(end);
end
2.2.2 主函数程序
clc; clear;
syms x y
F(x,y) = tan(x^2 + y^2);
a = 0;
b = pi/3;
c = 0;
d = pi/6;
epsilon = 0.5e-5;
result = trapezoid(a,b,c,d,F,epsilon);