GNN Algorithms (1): DeepWalk

目录

DeepWalk Concept

Random Walk

word2vec~CBOW model

word2vec~skip-gram model

skip-gram steps

loss function

BP 

optimizing Computational Efficiency

Conclusion

Problem & Solution

Thinking

DeepWalk Algorithms

steps

conclusion

Thinking

DeepWalk Codes

1. 定义节点和邻接矩阵

2. 定义random walk函数

3. 搭建前馈神经网络模块

4. 定义skip-grawm函数

---

DeepWalk Concept

图表示Graph Embedding based on Random Walk

-> Graph GNN based neighbor aggregation. 

Graph Embedding使用低维稠密向量的形式表示图中的节点，使得在原始图中相似的节点在低维表达空间中也相似。

DeepWalk关键基础是Random Walk和word2vec，word2vec关键基础是SkipGram

->DeepWalk通过Random Walk方式在图中进行节点采样

-> node sequence来模拟语料库中的语料，进而使用word2vec学习图中节点与节点的共线关系

-> 相邻节点的权重矩阵，进而学习到节点的向量表示。

Random Walk

Random Walk用于随机生成一条节点序列node sequence。

随机游走是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点，从其邻居中随机采样节点作为下一个访问节点，重复此过程，直到访问序列长度满足预设条件。

word2vec~CBOW model

词袋模型，CBOW的目标是根据上下文contextual words来预测当前中心词的概率，且上下文所有单词对当前中心词出现的概率影响权重是一样的，如在袋子中取词，取出足够数量的词就可以了，与取出词的先后顺序无关。

word2vec~skip-gram model

参考：Neural Network-神经网络算法本质_天狼啸月1990的博客-CSDN博客

根据中心词来预测上下文词概率。

V，语料库词汇量

N，隐藏层神经单元数量 = word embedding size

C，窗口大小，是预测单词的最大的上下文位置，那么总共的上下文词位置数目K=2c，比如预测上下文单词窗口为2，那么我们将会在(t-2), (t-1), (t+1), (t+2)的上下文位置预测contextual word。

|v|，输入向量维度，one-hot编码

[|v|, N]，hidden layer权重矩阵W的维度，权重矩阵每一列对应着一个神经元，执行Σ加权求和操作。

H[N]，hidden layer输出向量，维度是N。

W’，输出层的权重矩阵，维度是[N, |v|]。

U，输出层的输出向量，概率向量，维度是|v|，没有激活成0-1向量。

输入：only one中心词v-dimensional one-hot向量。

输出：2*c上下文词的one-hot vectors！

w(t)是中心词，也叫输入词input word，其中只有一个隐藏层，它执行权重矩阵和输入向量w(t)之间的点积运算。隐藏层中不需要使用激活函数。

然后，隐藏层中的点积运算结果被传送到输出层，输出层计算隐藏层输出向量和输出层权重矩阵之间的点积。

最后，使用softmax函数来计算在给定上下文位置中，输出层输出单词向量出现在w(t)上下文中的概率。

skip-gram steps

1) 利用one-hot编码将语料库单词转化为one-hot向量，这些向量维度[1,|V|]。

2) 输入中心词one-hot向量w(t)从|v|神经元被传递到hidden layer

3) 隐藏层执行权重矩阵W[|V|, N]和输入向量w(t)之间的点积运算。[1, V]*[V, N] -> [1, N]隐藏层不适用激活函数，所以H会直接传递到输出层。

4) 输出层执行H[1,N]和输出权重矩阵W'之间的点积运算，得到output vector u

5) 使用softmax函数，得到激活后的输出相邻output vector y。

如果要预测2c=K个上下文位置的contextual words，那么对于一个给定中心词w(t)，要生成K个相同的contextual word vector，与真实的K个one-hot vector对比，继而进行反向传播更新权重，那么对于语料库中v个单词，总共的计算次数为|v|*K。

6) 通过交叉熵损失函数loss function来进行BP反向传播，更新权重矩阵W和W'。

 是在第c个上下文位置上预测第j个单词 -> softmax后输出向量第j个分量概率代表该上下文位置是语料库中第j个单词的概率，因为第j个单词的one-hot向量是根据索引j生成的，正好对应输出向量j分量的概率。

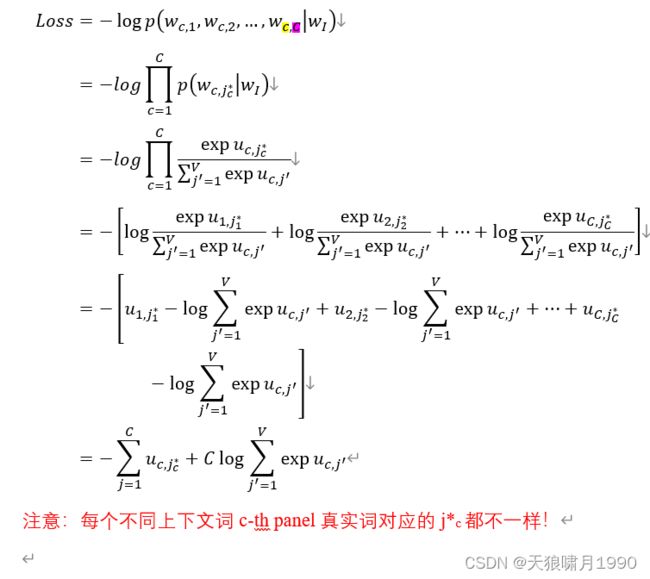
loss function

对于多个上下文词的输出向量，因为各个上下文词之间相互独立，则损失函数等于各个panel概率相乘。

且每个上下文概率计算过程中，只有一个，不妨记作，其余=0.

BP 

• 从输出层到隐藏层：更新权重

对于每天由deepwalk生成的node sequence，每个训练样本()，都需要使用上述公式更新词典中每个词的输出向量。在更新每个词向量时，需要收集该词在不同上下文cth-panel位置上的误差和，然后进行更新。一共需要V*k(k=2c)次更新。

• 从隐藏层到输入层。

Notice：skip-gram每次更新隐层权重W，只更新one-hot输入向量ti=1分量对应的那一行wi权重，其他权重因为xk=0而无法进行更新。

每次更新输出权重W'，for each c-th panel contextual word，需要更新V个单词概率。

problem：计算成本高，特别是对于大型词汇表，输出层权重矩阵W'的更新方式是不切实际的。

solution：限制必须要更新训练样例的输出向量W'的数目。

optimizing Computational Efficiency

Analysis:这种复杂性主要原因是我们采用多分类建模形式，共V个类。即认为要预测的单词是在所有单词上的多项式分布，那么肯定要拟合所有的概率值。

Ideas：

1) 将多分类改成多个二分类，同时要能够很好很快地计算训练样本实例得到似然值 -> hierarchical softmax

2) 每次训练一个样本实例的时候，不全部优化所有单词得输出向量，而是有代表性的优化某些输出向量 -> negative sampling

=> 这两种方法通过只优化输出向量更新的计算过程来实现的。

1. Hierarchical softmax

本质：用整棵二叉树充当输出层的角色。输入层到隐层和skip-gram结构类似，隐层神经元和二叉树所有内部节点都有连接，来传递向量h。

Concept:

        Hierarchical softmax是一种有效计算softmax的方式。该模型使用一颗二叉树来表示词汇表中的所有单词。所有的V都在二叉树的叶子节点上，可以证明非叶子节点一共有V-1个。对于每个叶子节点，从根节点root到该叶子节点只有一条路径，这条路径用来评估该叶子节点代表单词的概率值。二叉树结构如下图：

       在hierarchical softmax模型中，所有的单词没有输出向量表示形式，不同的是，二叉树的每一个内部节点都有一个输出向量V’n(w,j)。在迭代更新每一个训练样本(wI, wo)时，不需要优化所有V-1个非叶子节点对应的输出向量，只需要更新从根节点到训练样本输出词wo路径上经过的O(logV)量级个非叶子节点的输出向量。

1. Negative sampling

本质：用一部分有代表性的词代表所有输出向量词进行更新权重。其中，最终输出的上下文词(正样本)在采样过程中应该保留下来并进行更新，同时我们需要采集一些单词作为负样本(negative sampling)。在采样过程中，可以任意选择一种概率分布，将这种概率分布称为“噪声分布”(noise distribution)，用Pn(w)来表示。在word2vec中，作者使用了一种简单的unigram distribution。

Conclusion

• Skip-gram优缺点

优点：

无监督，可以用于任何文本

相比其他的单词转向量法，skip-gram需要的memory更少。

它只需要两个维度[N, |v|]，通常情况下，N约为300，|v|约为数百万。

缺点：

       找到N和C的最佳值很困难

       Softmax计算耗费时间很长

       训练这个算法耗时较长

• Skip-gram算法目的是在给定单词的条件下，计算上下文单词出现的概率。
• 通过skip-gram将单词转换为向量，能够融合单词的上下文语义信息，使语义相似单词的向量在嵌入空间中距离很近

word2vec，根据skip-gram训练好hidden layer权重矩阵W后，仅保留hidden layer权重矩阵W生成的embedding vector就是word2vec向量。

• Skip-gram输入层到隐藏层和CBOW一样。隐藏层到输出层输出c个多项式分布，每个多项式分布代表第c个上下文位置(c-th panel)上所有单词的概率分布，并且W’由c个上下文panel共享à即c个多项式相同。

Problem & Solution

计算成本高，如果我们又10000个单词的词汇表，想嵌入300维词向量，那么权重矩阵有10000 * 300个参数，在如此庞大的神经网络中进行梯度下降是很慢的！

Solution:

1. 单个词组成词组；删除停用词
2. 对高频词进行抽样来减少训练样本个数。
3. ‘negative sampling’抽取5-10个负样本只更新一小部分权重，从而降低计算负担。Because training需要输入训练样本并不断调整全部神经元的权重，而且每经过一个训练样本的训练，它的权重就进行一次调整。

Thinking

上述降低计算成本的第二项解决方法，高频词不一定是最有意义的单词，可以根据TF·IDF来抽取最有意义的单词，来降低词汇量。

DeepWalk Algorithms

DeepWalk算法包括两个步骤：

1. 第一步为随机游走采样节点序列。构建同构网络heterogeneous graph，从网络中的每个节点开始分别进行Random Walk采样，得到局部相关联的训练数据。
2. 第二部为使用word2vec based on skip-gram学习表达向量。对采样数据进行skipgram训练，将离散的网络节点表示成向量化，最大化节点共现，à使用Hierarchical softmax来做超大规模分类的分类器。

Shuffle，洗牌，表示随机化顺序，避免数据投入顺序对网络训练造成影响，避免训练陷入局部最优化。数据集一定充分打散(shuffle)

steps

DeepWalk中的Random Walk生成node sequence

• skip-gram: 中心点vi预测上下序列位置节点的one-hot向量vector’
• 预测节点概率向量与真实序列该位置节点的one-hot vector的损失函数，进行反向传播
• move to next vertex and continue training

conclusion

1. deepwalk用于将graph节点向量化以便后续的深度学习
2. random walk得到一条node sequence，如果将其当做一个句子，那么节点为句子中的word。

Thinking

Question:

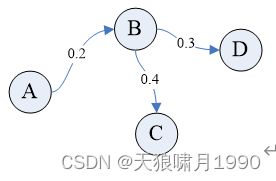
Random Walk得到的序列node sequence并没有体现出节点间连接connection的权重，即Random Walk随机得到的node sequence并不一定是连接最紧密(概率最高)的节点序列，那么用其来进行反向传播backward，是否是权重矩阵W最合适的方式。

如果提升节点序列顺序，是否会优化word embedding效果？

 

比如：Random Walk可能生存1条node sequence：A->B->D，但连接最紧密的A->B->D是否更有助于BP和更新权重矩阵W?

DeepWalk Codes

1. 定义节点和邻接矩阵

import os
project_path = os.getcwd()

import numpy as np
import pandas as pd

import torch
import torch.nn as nn
import random

adj_list = [[1,2,3],[0,2,3],[0,1,3],[0,1,2],[5,6],[4,6],[4,5],[1,3]]
size_vertex = len(adj_list) # number of vertices

w = 3 # window size
d = 2 # embedding size
y = 200 # walks per ventext
t = 6 # walk length
lr = 0.025 # learning rate

2. 定义random walk函数

def RandomWalk(node, t):
    walk = [node]

    for i in range(t - 1):
        list_length = len(adj_list[node])-1
        node_index = random.randint(0, list_length)
        node = adj_list[node][node_index]
        walk.append(node)
    return walk

3. 搭建前馈神经网络模块

class Model(torch.nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.phi = nn.Parameter(torch.rand((size_vertex, d), requires_grad=True))  # size_vertex是one-hot向量维度，d是word embedding维度
        self.phi2 = nn.Parameter(torch.rand((d, size_vertex), requires_grad=True))

    def forward(self, one_hot):
        hidden = torch.matmul(one_hot, self.phi)
        out = torch.matmul(hidden, self.phi2)
        return out

model = Model()

4. 定义skip-grawm函数

def skip_gram(wvi, w):
    # wvi表示random walk生成的node sequence；w = 3 window size
    for j in range(len(wvi)):

        # # 计算上下文词数量C
        # c = min(j + w + 1, len(wvi)) - max(0, j - w)

        # 损失函数loss=每个panel的第ti=1那个位置误差error之和
        # generate one hot vector
        one_hot = torch.zeros(size_vertex)
        one_hot[wvi[j]] = 1  # 中心词输入one-hot向量
        # 未激活的输出向量
        out = model(one_hot)

        loss = 0
        # for c-th panel
        for k in range(max(0, j - w), min(j + w + 1, len(wvi))):  # 确定中心点j左右范围，k遍历中心点j的左右位置
            # 损失函数e=每个panel的第j个位置误差之和
            error = torch.log(torch.sum(torch.exp(out))) - out[wvi[k]]
            loss += error
        loss.backward()

        for param in model.parameters():
            param.data.sub_(lr * param.grad)
            param.grad.data.zero_() # param.grad就是每次迭代计算的误差error，需要每次重置为0