如何使用scipy.stats快速对统计量拟合多种统计分布并进行可视化

由于我们在对统计量统计频率后，往往需要对统计量拟合其合适的分布，但scipy.stats提供了超过80种的统计分布，我们不可能手工对其进行尝试，因此以下代码将选择多种常用的统计分布快速对统计量进行拟合，并通过卡方检验返回其最适合的3种分布以及其对应的参数，最后将统计量的分布与其拟合的分布进行可视化。

1. 载入数据，并将数据进行array化

import pandas as pd
import numpy as np
import scipy
from sklearn.preprocessing import StandardScaler
import scipy.stats
import matplotlib.pyplot as plt
%matplotlib inline
# Load data and select first column

from sklearn import datasets
y=np.array(df_test.week)

# Create an index array (x) for data

x = np.arange(len(y))
size = len(y)

2. 进行统计量的分布展示

plt.hist(y)
plt.show()

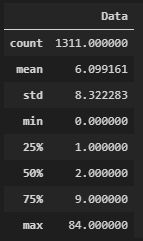
3. 展示统计量的统计概况

y_df = pd.DataFrame(y, columns=['Data'])
y_df.describe()

4. 对数据进行标准化

sc=StandardScaler() 
yy = y.reshape (-1,1)
sc.fit(yy)
y_std =sc.transform(yy)
y_std = y_std.flatten()
y_std
del yy

5. 快速拟合10种分布并进行卡方检验，再从高到低返回最合适的分布，卡方值和p值，最后用最大似然函数返回最合适的3种分布所对应的参数。

注意：
由于卡方检验中，在计算期望频率的数组中可能会出现NaN，如果不进行处理，将使得累计的期望频率和（cum_expected_frequency）也计算为NaN，进而导致卡方检验值为空，故在这里需要对NaN进行替换，因此可考虑填0来替换NaN值 （在下列代码中有进行标注）。

# Set list of distributions to test
# See https://docs.scipy.org/doc/scipy/reference/stats.html for more

# Turn off code warnings (this is not recommended for routine use)
import warnings
warnings.filterwarnings("ignore")

# Set up list of candidate distributions to use
# See https://docs.scipy.org/doc/scipy/reference/stats.html for more

dist_names = ['beta',
              'expon',
              'gamma',
              'lognorm',
              'norm',
              'pearson3',
              'triang',
              'uniform',
              'weibull_min', 
              'weibull_max']

# Set up empty lists to stroe results
chi_square = []
p_values = []

# Set up 50 bins for chi-square test
# Observed data will be approximately evenly distrubuted aross all bins
percentile_bins = np.linspace(0,100,51)
percentile_cutoffs = np.percentile(y_std, percentile_bins)
observed_frequency, bins = (np.histogram(y_std, bins=percentile_cutoffs))
cum_observed_frequency = np.cumsum(observed_frequency)

# Loop through candidate distributions

for distribution in dist_names:
    # Set up distribution and get fitted distribution parameters
    dist = getattr(scipy.stats, distribution)
    param = dist.fit(y_std)
    
    # Obtain the KS test P statistic, round it to 5 decimal places
    p = scipy.stats.kstest(y_std, distribution, args=param)[1]
    p = np.around(p, 5)
    p_values.append(p)    
    
    # Get expected counts in percentile bins
    # This is based on a 'cumulative distrubution function' (cdf)
    cdf_fitted = dist.cdf(percentile_cutoffs, *param[:-2], loc=param[-2], 
                          scale=param[-1])
    expected_frequency = []
    for bin in range(len(percentile_bins)-1):
        expected_cdf_area = cdf_fitted[bin+1] - cdf_fitted[bin]
        expected_frequency.append(expected_cdf_area)
    
    # calculate chi-squared
    expected_frequency = np.array(expected_frequency) * size
    cum_expected_frequency = np.cumsum(expected_frequency)
    
    # 注意：由于cum_expected_frequency的数组中可能会出现NaN，如果不替换NaN，将无法返回卡方的结果，故在这里需要对NaN进行替换，我这里替换的方式是填0。
    l = ((cum_expected_frequency - cum_observed_frequency) ** 2) / cum_observed_frequency
    l[np.isnan(l)] = 0
    ss = sum (((cum_expected_frequency - cum_observed_frequency) ** 2) / cum_observed_frequency)
    chi_square.append(ss)
        
# Collate results and sort by goodness of fit (best at top)

results = pd.DataFrame()
results['Distribution'] = dist_names
results['chi_square'] = chi_square
results['p_value'] = p_values
results.sort_values(['chi_square'], inplace=True)
    
# Report results

print ('\nDistributions sorted by goodness of fit:')
print ('----------------------------------------')
print (results)

如下图可知，对于这里的统计量，最合适的分布是指数分布。

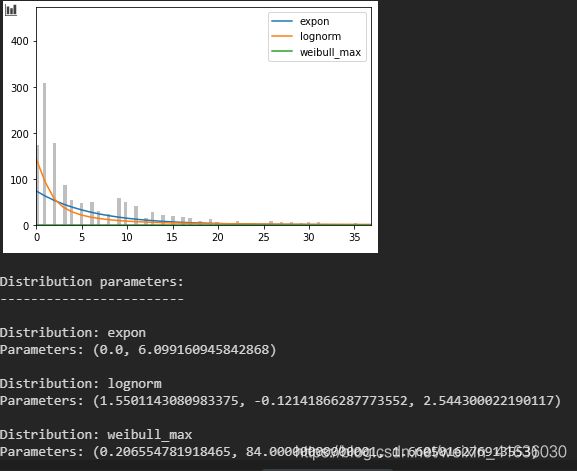
6. 将前3种分布与统计量进行拟合画图，并返回对应的参数值

# Divide the observed data into 100 bins for plotting (this can be changed)
number_of_bins = 100
bin_cutoffs = np.linspace(np.percentile(y,0), np.percentile(y,99),number_of_bins)

# Create the plot
h = plt.hist(y, bins = bin_cutoffs, color='0.75')

# Get the top three distributions from the previous phase
number_distributions_to_plot = 3
dist_names = results['Distribution'].iloc[0:number_distributions_to_plot]

# Create an empty list to stroe fitted distribution parameters
parameters = []

# Loop through the distributions ot get line fit and paraemters

for dist_name in dist_names:
    # Set up distribution and store distribution paraemters
    dist = getattr(scipy.stats, dist_name)
    param = dist.fit(y)
    parameters.append(param)
    
    # Get line for each distribution (and scale to match observed data)
    pdf_fitted = dist.pdf(x, *param[:-2], loc=param[-2], scale=param[-1])
    scale_pdf = np.trapz (h[0], h[1][:-1]) / np.trapz (pdf_fitted, x)
    pdf_fitted *= scale_pdf
    
    # Add the line to the plot
    plt.plot(pdf_fitted, label=dist_name)
    
    # Set the plot x axis to contain 99% of the data
    # This can be removed, but sometimes outlier data makes the plot less clear
    plt.xlim(0,np.percentile(y,99))

# Add legend and display plot

plt.legend()
plt.show()

# Store distribution paraemters in a dataframe (this could also be saved)
dist_parameters = pd.DataFrame()
dist_parameters['Distribution'] = (
        results['Distribution'].iloc[0:number_distributions_to_plot])
dist_parameters['Distribution parameters'] = parameters

# Print parameter results
print ('\nDistribution parameters:')
print ('------------------------')

for index, row in dist_parameters.iterrows():
    print ('\nDistribution:', row[0])
    print ('Parameters:', row[1] )

结果展示：
由下图可知，指数分布表现最好，且通过MLE估计出其参数为（0.0, 6.01）。

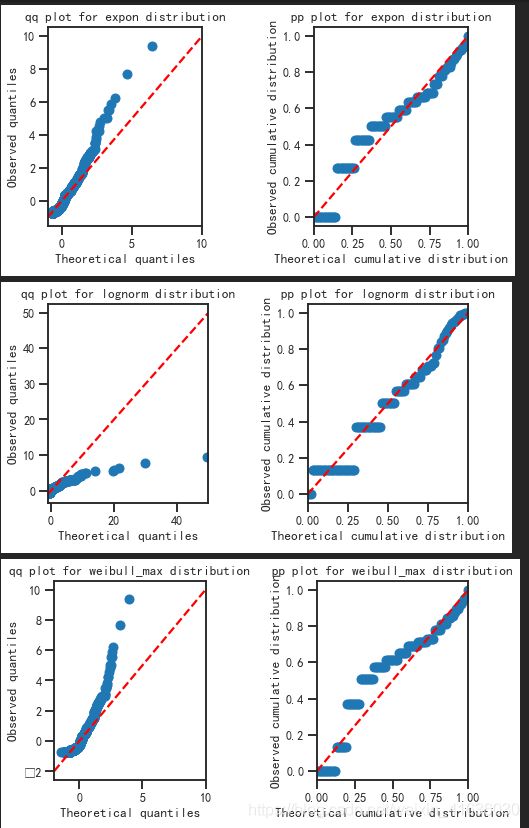
7. 用qq和pp plot去检验该分布有多适合当前的统计量

## qq and pp plots
    
data = y_std.copy()
data.sort()

# Loop through selected distributions (as previously selected)

for distribution in dist_names:
    # Set up distribution
    dist = getattr(scipy.stats, distribution)
    param = dist.fit(y_std)
    
    # Get random numbers from distribution
    norm = dist.rvs(*param[0:-2],loc=param[-2], scale=param[-1],size = size)
    norm.sort()
    
    # Create figure
    fig = plt.figure(figsize=(8,5)) 
    
    # qq plot
    ax1 = fig.add_subplot(121) # Grid of 2x2, this is suplot 1
    ax1.plot(norm,data,"o")
    min_value = np.floor(min(min(norm),min(data)))
    max_value = np.ceil(max(max(norm),max(data)))
    ax1.plot([min_value,max_value],[min_value,max_value],'r--')
    ax1.set_xlim(min_value,max_value)
    ax1.set_xlabel('Theoretical quantiles')
    ax1.set_ylabel('Observed quantiles')
    title = 'qq plot for ' + distribution +' distribution'
    ax1.set_title(title)
    
    # pp plot
    ax2 = fig.add_subplot(122)
    
    # Calculate cumulative distributions
    bins = np.percentile(norm,range(0,101))
    data_counts, bins = np.histogram(data,bins)
    norm_counts, bins = np.histogram(norm,bins)
    cum_data = np.cumsum(data_counts)
    cum_norm = np.cumsum(norm_counts)
    cum_data = cum_data / max(cum_data)
    cum_norm = cum_norm / max(cum_norm)
    
    # plot
    ax2.plot(cum_norm,cum_data,"o")
    min_value = np.floor(min(min(cum_norm),min(cum_data)))
    max_value = np.ceil(max(max(cum_norm),max(cum_data)))
    ax2.plot([min_value,max_value],[min_value,max_value],'r--')
    ax2.set_xlim(min_value,max_value)
    ax2.set_xlabel('Theoretical cumulative distribution')
    ax2.set_ylabel('Observed cumulative distribution')
    title = 'pp plot for ' + distribution +' distribution'
    ax2.set_title(title)
    
    # Display plot    
    plt.tight_layout(pad=4)
    plt.show()

结果展示：
从下图的qqplot可以看出，指数分布将更加适合当前的统计量

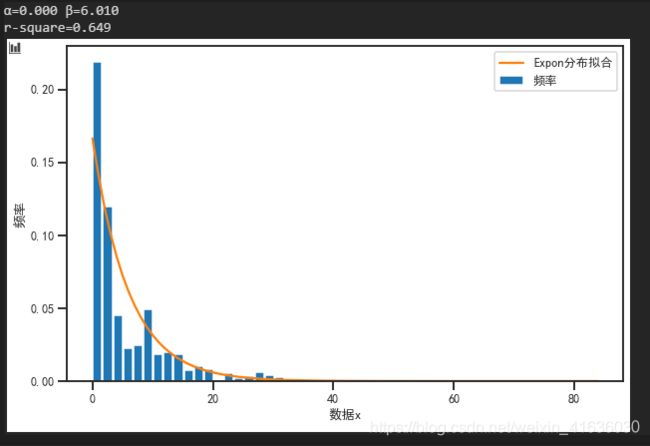
8. 对统计量与拟合的概率分布进行可视化对比

import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as st
import numpy as np


class Exponfitplot:
    def __init__(self, x, num_bins, legends=None, labels=None, fsize=(10, 6.18), show_info=True):
        #:param x: 数据x列表
        #:param num_bins: x的分组数
        #:param legends: 图例名，默认为 "频率", "Expon分布拟合"
        #:param labels:坐标轴标题名，默认为 "数据x", "数据y"
        #:param show_info:是否显示拟合结果信息
        if legends is None:
            legends = ["频率", "Expon分布拟合"]
        if labels is None:
            labels = ["数据x", "频率"]
        self.x = x
        self.num_bins = num_bins
        self.paras = (0, 6.01)
        self.fsize = fsize
        self.legends = legends
        self.labels = labels
        self.show_info = show_info

    def change_legend(self, new_legends):
        # 更改图例
        self.legends = new_legends

    def change_label(self, new_labels):
        # 更改坐标轴标题
        self.labels = new_labels

    def change_para(self, new_paras):
        # 更改gamma分布的参数
        self.paras = new_paras

    def draw_plot(self):
        fs = self.fsize  # 画布大小
        # alpha = self.paras[0]  # gamma分布中的参数α
        # beta = self.paras[1]  # gamma分布中的参数β

        # 利用seaborn库对字体大小进行统一设置，为fgsize[1]的0.12倍，即画布纵向大小为1000时，font_scale=1.2
        sns.set_style("ticks")
        sns.set_context("talk", font_scale=fs[1]*0.12)
        plt.rcParams['font.sans-serif'] = ['SimHei']

        # 设置画布
        plt.figure(figsize=fs)

        # ax:绘制频率直方图
        plt.hist(self.x, self.num_bins, density=1, rwidth=0.9, label=self.legends[0])
        plt.xlabel(self.labels[0])
        plt.ylabel(self.labels[1])

        # ax2:绘制gamma拟合曲线
        self.x.sort()
        y = st.expon.pdf(self.x, 0, scale=6.01)
        plt.plot(self.x, y, '-', label=self.legends[1])
        if self.show_info:
            info = "α={:.3f} β={:.3f}\nr-square={:.3f}".format(self.paras[0], self.paras[1], st.linregress(self.x, y)[2]**2)
            print(info)
        # 显示多图例
        plt.legend(loc=1, bbox_to_anchor=(1, 1))


if __name__ == "__main__":
    np.random.seed(19680801)
    iqs = np.array(df_test.week) # 待绘制直方图的数据
    bins = 50  # 数据分组数
    gammaplot = Exponfitplot(iqs, bins)
    gammaplot.draw_plot()
    plt.show()

结果展示：
从下图中可以看出，expon(x, loc= 0, scale = 6.01) 的指数分布对于该统计量的拟合效果比较好

9. 校验：定义该指数函数，并根据统计量的值返回对应的指数分布的概率

f_0 = scipy.stats.expon.pdf(0, loc = 0, scale = 6.01)
print('the probablity of exponential distribution is {0} when x = 0'.format(f_0))

结果展示：