论文《Context Contrasted Feature and Gated Multi-scale Aggregation for Scene Segmentation》笔记
 论文来自 CVPR2018
论文来自 CVPR2018
代码:https://github.com/henghuiding/CCL
出发点
深度卷积神经网络在语义分割中,明显目标的特征会占主导地位,导致不明显地物的信息被弱化或忽略。背景信息是场景分割的关键,并且有很多工作关注了这一点。但是,上下文信息通常有更平滑的表征并会被明显目标所主导,这对不明显目标的识别是有害的。
因此,本文提出了 Context contrasted local features 以更好地利用上下文信息同时从背景信息中关注局部信息;进一步地,使用了一个 context contrasted based local(CCL) 模型获得多尺度和多等级的 context contrasted local features。除此之外,因为传统的多尺度信息融合的方法有(1)多尺度输入(2)跳跃连接。但是已有的使用跳跃连接的网络只是简单的对特征进行相加融合,因此不同尺度的重要性差异被忽略。所以本文提出了一个选择(门控)相加机制(choice mechanism)【听起来可能有点难理解,但作者后面有解释为什么使用 ”gates“ 以和简单的固定值和可学习参数区分开来】 以更好地控制多尺度信息的融合。
多尺度融合
本文首次提出在单个网络中使用门控相加来选择性地融合特征。
网络结构如下图所示
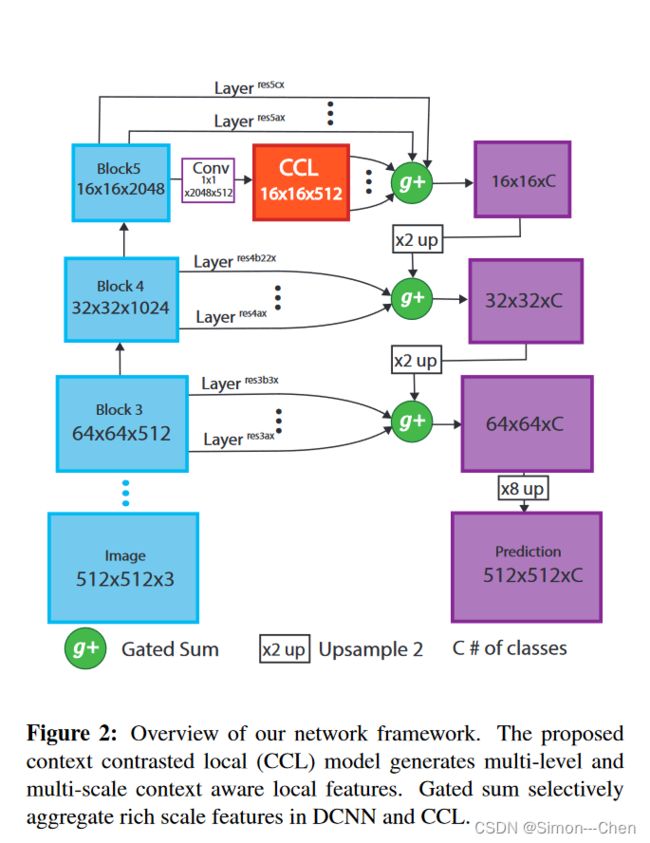
模型包含一个 CCL 模块用来产生顾及背景环境的多尺度和多级别的特征,以及一个门控融合模块用于选择性地融合多个尺度的特征。
场景分割中的目标非常复杂,不加区分地采集背景信息将带来噪声,如下图所示,与图中的两个人相比,身后的汽车属于不明显目标,从像素 A 附近收集的 local(局部) 特征对于其它像素来说是可分的,但是没有考虑到全局信息如建筑物和道路,这可能无法为像素 A 获得鲁棒的高级语义特征。然而,如图中第一行第三个小图所示,融合背景将会带来处于主导位置的对象(图中的人)的特征,因此汽车上像素的特征(如 Pixel A) 会被人的特征所淹没(dominated),汽车的一些信息将会在最终的预测层被忽略,导致错误的预测结果。不同位置的上下文信息容易被明显地物特征所主导。
因此,要对 Pixel A采集合适和具有可分性的高级特征是非常困难的,为了解决这一问题,本文提出将局部信息和上下文信息的生成分开,然后通过局部特征和上下文特征的对比(相减)来融合两个信息:
C L = F l ( F , Θ l ) − F c ( F , Θ c ) CL = F_l(F, \Theta_l) - F_c(F, \Theta_c) CL=Fl(F,Θl)−Fc(F,Θc)
F 为输入的特征, F l F_l Fl 是 local convolution 的函数, F c F_c Fc 代表的是上下文特征的 convolution, Θ l \Theta_l Θl 和 Θ c \Theta_c Θc 分别为两者的参数, CL 为得到的 context contrasted local features.

局部信息和分离的背景信息之间的对比,不仅可以利用有用的背景信息,而且能够通过与背景信息的对比强调局部信息(上图第二行图三)。
Context Contrasted Local (CCL) Model
CCL模型如下图所示

CCL 由多个连续的 context-local 模块(上图第二行)组成。使用门控相加来选择性地融合不同级别的 context contrasted local features。 CCL 中每一个 Context-local 模块首先使用两个不同的空洞率的卷积获取不同尺度的特征,同时获得上下文和局部信息,通过相减获得 context-contrasted local features, 然后通过一个门控相加对多尺度特征进行融合得到 score map(概率图)。
Gated Multi-scale Aggregation (门控多尺度融合)
使用 skip layers (跳跃连接层)对不同尺度的特征进行简单的相加,只是不加选择地汇集不同跳跃连接层的信息,有些甚至是不适合或者对分类效果有害的。简单说就是,没有对特征进行选择。
本文提出了使用门控相加(gated sum) 来选择不同尺度的特征,如下图所示

本文使用门控相加的主要动机是,让网络基于特征图的尺度自适应地决定适每个像素的感受野。gated sum 可以使得网络自己根据特征图的信息,选择融合那些尺度的特征图。
如上图所示,假设 来自不同尺度的特征 F p n \Bbb F_p^n Fpn, 通过 N 个跳跃连接层 产生了 N 个 得分图(score maps, 经过sigmoid/Softmax 可得到概率图) S p c , n \Bbb S_p^{c,n} Spc,n,也就是说:
S p c , n = F s n ( F p n , Θ s n ) \Bbb S_p^{c,n} = \cal F_s^n(\Bbb F_p^n, \Theta_s^n) Spc,n=Fsn(Fpn,Θsn)
p 表示来自网络不同位置的特征; n ∈ 1 , 2 , . . . , N n \in {1,2,...,N} n∈1,2,...,N; c ∈ 1 , 2 , . . . , C c \in {1,2,...,C} c∈1,2,...,C ,并且 C C C 是类别数;
F s n 是 \cal F_s^n 是 Fsn是 第 n 层跳跃层的分类器函数, Θ s n \Theta_s^n Θsn 对应分类器的参数。
F n p \Bbb F_n^p Fnp 是维度为 H × W × # C h a n n e l s H \times W \times \#Channels H×W×#Channels 的输入特征 。
对于每一个 skip layer, 首先产生一个形状为 H × W × 1 H \times W \times 1 H×W×1 的概率图 I p n \Bbb I_p^n Ipn
I n p = F i n ( F p n , Θ i n ) \Bbb I_n^p = \cal F_i^n(\Bbb F_p^n,\Theta_i^n) Inp=Fin(Fpn,Θin)
F i n \cal F_i^n Fin 是第 n 个 Conv+Sigmoid 层(本文称之为 info-skip 层), Θ i n \Theta_i^n Θin为对应的参数
因为这些不同位置的跳跃层获得的 得分图和信息图 是在同一个 DCNN 内的,也就是说,这些特征图之间的从低级到高级的序列关系应该要考虑进来
所以本文采用 RNN 来学习序列关系,基于 RNN,获得不同尺度特征图之间的序列关系。
接着,得到的信息图 I p n \Bbb I_p^n Ipn 被以序列的形式输入 RNN 来学习它们之间的关系
h p n = t a n h ( W n ( I p n h p n − 1 ) h_p^n = tanh(W^n(_{\Bbb I_p^n}^{h_p^{n-1}}) hpn=tanh(Wn(Ipnhpn−1)
h p n h_p^n hpn 是 RNN 的第 n 个输出。为了使网络更加高效,所有位置的输出计算都是并行的, W n W^n Wn 是所有位置的共享参数。
(上图中的 Global Refine 模块)为了使每一个信息图都可以关注到全局信息,对 RNN 的输出进行拼接, H p = ( h p 1 . . . h p N ) T H_p = (h_p^1...h_p^N)^T Hp=(hp1...hpN)T, 然后通过全局信息进行优化:
H ‾ p = F g ( H p , Θ g ) + H p \overline H_p = \cal F_g (\it H_p, \Theta_g) + H_p Hp=Fg(Hp,Θg)+Hp
F g \cal F_g Fg 是一个 1 x 1 x N x N 的 Conv, Θ g \Theta_g Θg 是对应的参数。
然后将 H ‾ p \overline H_p Hp 分开, H ‾ p = ( h ‾ p 1 . . . h ‾ p N ) T \overline H_p = (\overline h_{p}^{1}...\overline h_p^{N})^T Hp=(hp1...hpN)T,并用于生成 gates G p n G_p^n Gpn
G p n = N ⋅ e h ‾ p n ∑ i = 1 N e h ‾ p i G_p^n = N \cdot \frac{e^{\overline h_p^n}}{\sum _{i=1}^Ne^{\overline h_p^i}} Gpn=N⋅∑i=1Nehpiehpn
每个位置 p 的 G p n G_p^n Gpn,被归一化至 N
最终,N 个特征图通过 gated sum 进行选择性地融合:
S ‾ p c = ∑ n = 1 N G p n S p c , n \overline {\Bbb S}_p^c = \sum_{n=1}^N G_p^n \Bbb S_p^{c,n} Spc=n=1∑NGpnSpc,n
S p c , n \Bbb S_p^{c,n} Spc,n 是不同尺度的特征经过分类器后得到的, S ‾ p c \overline {\Bbb S}_p^c Spc 为 gated sum 的输出
S p c , n \Bbb S_p^{c,n} Spc,n 有多少信息可以通过取决于 gates 值 G p n G_p^n Gpn, G p n G_p^n Gpn 越大,意味着对分类更有利。 G p n G_p^n Gpn 越小,意味着对于位置 p, 第 n 个 skip layer 的特征对分类帮助越低。
G p n G_p^n Gpn 好比一个权重,决定不同层的特征信息通过的程度
更重要的是,gates 的值 G p n G_p^n Gpn(上图中 Sum 模块的输入)不是一个固定的值,也不是直接从训练数据中学习来的。而是通过训练数据训练好的模型在测试数据上产生的, 所以, G p n G_p^n Gpn 不仅取决于训练数据,而且取决于输入的测试数据,并随着输入的特征图而变化。
因此,作者使用 “gates" 来表示和 固定值与学习参数的区别
sum: sum 是gated sum 的一个特例, gated sum 在 所有 gates 为 1 时,等同于 sum,
gated sum: 选择性地融合特征图,gates 值可以根据测试数据自适应地进行调整,控制 skip layer 的信息流通
为什么说 gates 值 G p n G_p^n Gpn 由训练数据和测试数据同时决定呢?
个人理解是,主要还是 Global Refine 模块中的 Normalization (归一化),归一化只需要用到输入特征图的统计信息,没有需要学习的参数。因此 G p n G_p^n Gpn 既取决于模型中训练得到的参数,也同时决定于测试数据的特征图。
Experiments
实验部分主要看图表就好,或者关注作者时如何做消融实验来验证自己提出的模块的,还有就是学习作者是如何分析的。
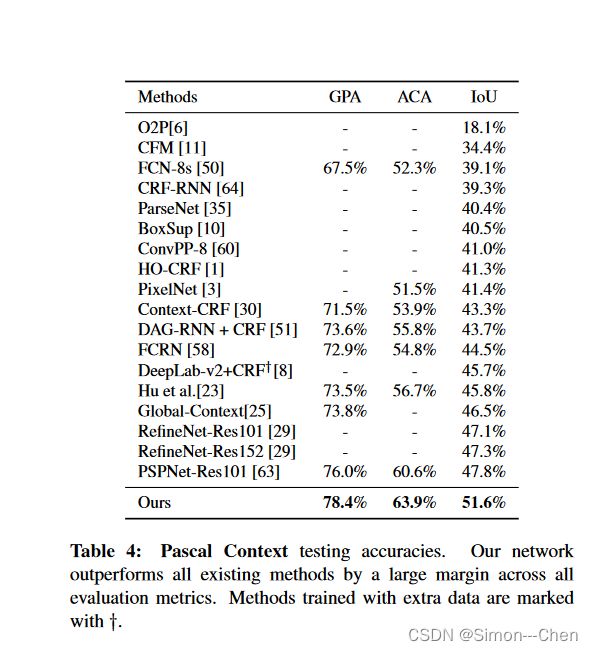
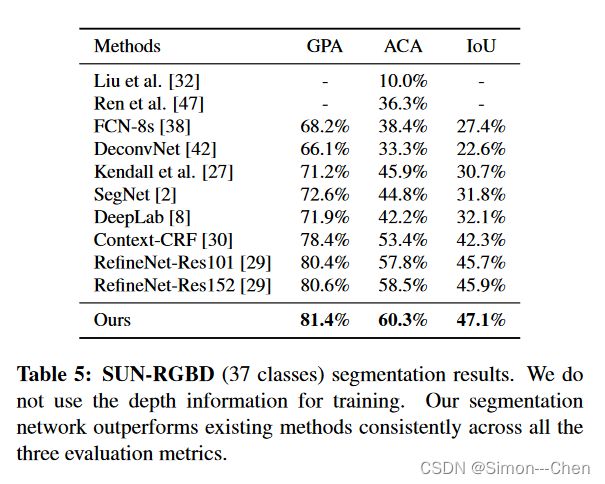
下表是与多尺度上下文信息提取模块 ASPP, CRF 以及 DAG-RNN 和 basline 的对比实验

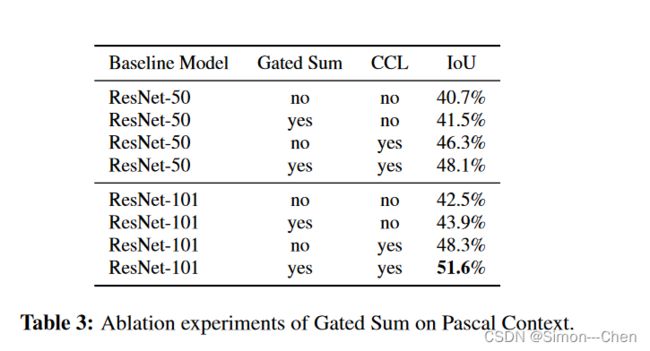
下表是 CCL 在 Pascal Context 数据集上的消融实验

门控相加的消融实验