Koch雪花曲线的MATLAB实现
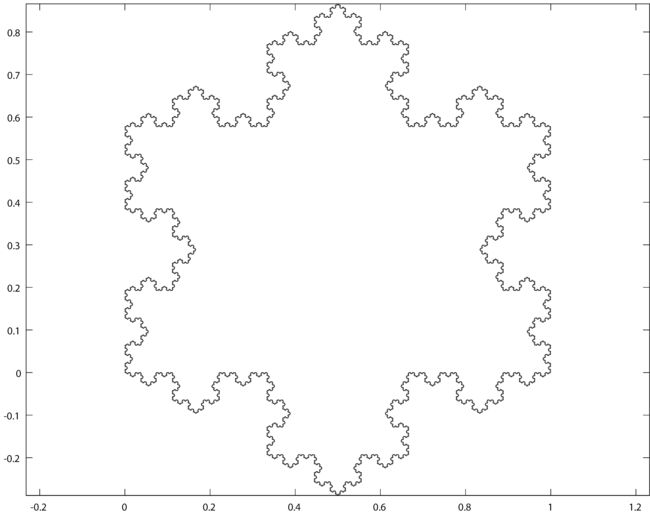
Koch曲线是分形图案的一个代表,对其研究很有意义,在此不敢多说。请见matrix67的博客:
http://www.matrix67.com/blog/archives/243
用一个复数序列代表整个图形,序列首尾相连,在复平面上的依次相连就构成了每一次的图形;对复数序列进行一次迭代,可以生成更细分的图形。下面分析迭代的计算过程。
迭代次数用n表示,映射 T x n ↦ x n + 1 T\mathbf x_n\mapsto \mathbf x_{n+1} Txn↦xn+1代表了从这一次的图形到下一次这个迭代过程,第n次的序列 x n = { x 1 , x 2 , ⋯ , x k n } ∈ C k n \mathbf x_n=\left\{\begin{matrix} x_1,x_2,\cdots,x_{k_n}\end{matrix}\right\}\in\Complex^{k_n} xn={x1,x2,⋯,xkn}∈Ckn,这里共有几个点是用 k n k_n kn来表示的。例如, n = 1 n=1 n=1时,代表初始的正三角形,复数序列 x 1 = { x 1 , x 2 , x 3 , x 1 } = { 0 , 1 , 1 / 2 ( 1 + 3 ı ) , 0 } \mathbf x_1=\left\{\begin{matrix} x_1,x_2,x_3,x_1\end{matrix}\right\}=\left\{\begin{matrix} 0,1,1/2(1+\sqrt 3\imath),0\end{matrix}\right\} x1={x1,x2,x3,x1}={0,1,1/2(1+3ı),0}。
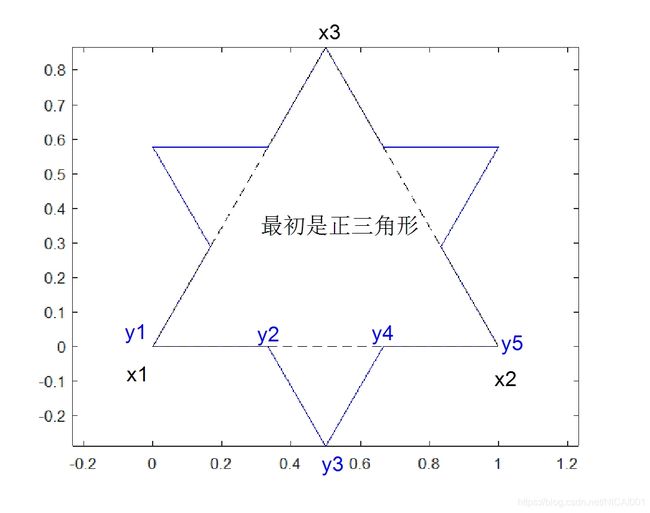
之所以用复数来表示,是为了方便对每一段进行映射。上图三角形的三条边,都是按照如下流程
- 等分三段,第1个点和第5个点与原来一样;
- 添加第2个点,在原矢量 x 1 → x 2 x_1\to x_2 x1→x2的 1 / 3 1/3 1/3处;
- 添加第3个点,矢量 y 2 → y 3 y_2 \to y_3 y2→y3长度不变,方向顺时针转 π / 3 \pi/3 π/3;
- 添加第4个点,在原矢量 x 1 → x 2 x_1\to x_2 x1→x2的 2 / 3 2/3 2/3处。
已知对复数乘以一个模值为1的复数 e ı θ e^{\imath \theta} eıθ可以改变其辐角,而不改变其大小,改变的方向是逆时针 θ rad \theta \text{rad} θrad。所以对第一段 x 1 → x 2 x_1\to x_2 x1→x2采取如下算法:
- Δ x = x 2 − x 1 \Delta x=x_2-x_1 Δx=x2−x1, y 1 = x 1 , y 5 = x 5 y_1=x_1,y_5=x_5 y1=x1,y5=x5
- y 2 = x 1 + 1 / 3 Δ x y_2=x_1+1/3\Delta x y2=x1+1/3Δx
- y 3 = y 2 + 1 3 e − π / 3 ı Δ x y_3=y_2+\frac1 3e^{-\pi/3\imath}\Delta x y3=y2+31e−π/3ıΔx
- y 4 = y 2 + 1 / 3 Δ x y_4=y_2+1/3\Delta x y4=y2+1/3Δx
至于总共有多少段,那不必要求证,关键是对上一个序列 x n = { x 1 , x 2 , ⋯ , x k n } \mathbf x_n=\left\{\begin{matrix} x_1,x_2,\cdots,x_{k_n}\end{matrix}\right\} xn={x1,x2,⋯,xkn}的每一个分段向量 x k → x k + 1 x_k\to x_{k+1} xk→xk+1都能进行如上计算。
Koch曲线代码
这个程序用MATLAB实现是极其简单的。
% Edited by NICAI001
% 通过复数曲线绘制Koch雪花
x_n=[1 (1+sqrt(3)*1i)/2 0 1];
slice=6; %这里是迭代次数
for n=1:slice
x_p=x_n;
lastSeg=length(x_n)-1;
for k=0:lastSeg-1
dX=(x_p(k+2)-x_p(k+1))/3;x_n(4*k+1)=x_p(k+1);
x_n(4*k+2)=x_p(k+1)+dX;
x_n(4*k+3)=x_n(4*k+2)+dX*(1/2-sqrt(3)*1i/2);
x_n(4*k+4)=x_p(k+1)+2*dX;
end
x_n(4*lastSeg+1)=x_p(lastSeg+1);
end
plot(x_n,'k--'),hold on;
axis equal;
类似地对代码稍作改动可以绘制以下图案
y=[1 1i+1 1i 0 1];
slice=5;
for k=1:slice;
x=y;n=length(x)-1;
for s=0:n-1
dz=(x(s+2)-x(s+1))/3;
y(5*s+1)=x(s+1);y(5*s+2)=x(s+1)+dz;
y(5*s+3)=y(5*s+2)-dz*1i;y(5*s+4)=y(5*s+3)+dz;
y(5*s+5)=y(5*s+4)+dz*1i;
end
y(5*n+1)=x(n+1);
end
plot(y),axis equal;
以上代码中y向量的初始值改成了正方形图案;dz没有变,仍然是原x向量三等分的值;但dz所乘的单位复数变为了-1i和1i,表示在dz方向上右偏或左偏90度;最后由于分割时原来一段上出现了5个点,最后要加上一个点 y(5)。
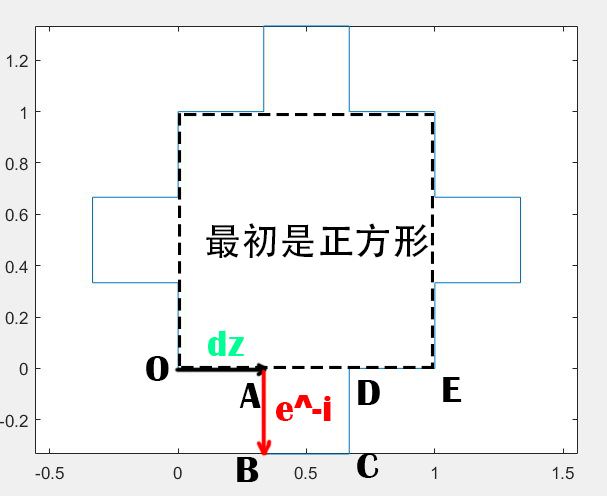
觉得之前的博客没有把问题说清楚,所以再来修改一下。

