【GIS开发】绘制三维数字地球(OpenGL、C++、glfw、glut)
文章目录
- 1、计算公式
- 2、绘图接口
-
- 2.1 glDrawArrays
- 2.2 glDrawElements
- 3、代码实现
- 4、运行结果(整体地球)
-
- 4.1 opengl / glut / c++ (3d)
- 4.2 opengl / glfw / glad / stb_image / c++ (3d)
- 4.3 opengl / glfw / glad / stb_image /c++ (3d,天空盒,高度贴图)
- 4.4 opengl / win32/ glew / FreeImage / c++ (3d,大气层)
- 4.5 opengl / freeglut / glew / FreeImage / c++ (3d,法线贴图)
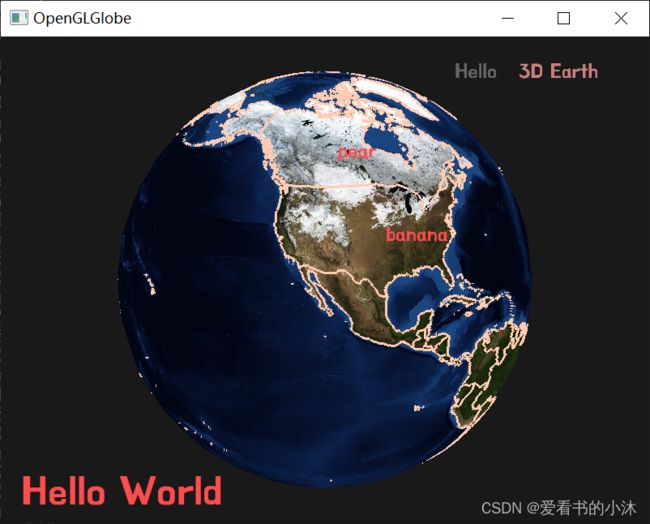
- 4.6 opengl / glfw / glad / stb_image / freetype / c++ (2d/3d,加载geojson)
- 4.7 opengl / glfw / glad / FreeImage / c++ (3d,白天层/黑夜层/云层)
- 5、运行结果(瓦片地球)
-
- 5.1 opengl / sdl / boost::asio / c++ (2d,瓦片贴图)
- 5.2 opengl / glfw / glew / curl / proj4 / gdal / stb_image / c++ (3d,瓦片贴图)
- 5.3 opengl / glfw / glad / boost::asio / proj4 / stb_image / c++ (3d,瓦片贴图)
- 结语
1、计算公式
球的三维坐标表示为:
x 2 + y 2 + z 2 = R 2 x^2 + y^2 + z^2 = R^2 x2+y2+z2=R2
引入球的参数坐标方程进行离散化。以(u,v)表示球面上某一点的坐标,且u,v的取值范围为[0 , 1],定义(u,v)到(x,y,z)的转换如下:
{ x = R × s i n ( π × v ) c o s ( 2 π × u ) y = R × s i n ( π × v ) s i n ( 2 π × u ) z = R × c o s ( π × v ) \begin{cases} x=R×sin(\pi×v)cos(2\pi×u) \\ y=R×sin(\pi×v)sin(2\pi×u) \\ z=R×cos(\pi×v) \end{cases} ⎩⎪⎨⎪⎧x=R×sin(π×v)cos(2π×u)y=R×sin(π×v)sin(2π×u)z=R×cos(π×v)
2、绘图接口
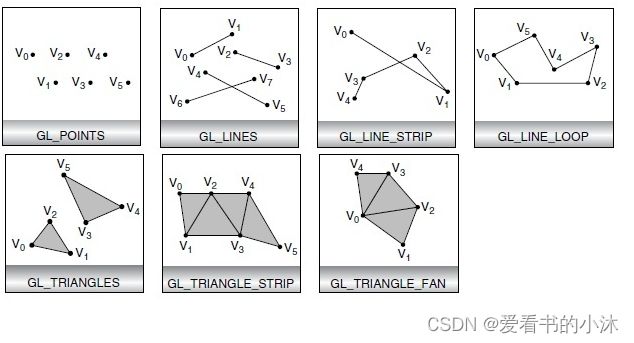
在OpenGL中,所有图形都是通过分解成三角形的方式进行绘制。
glDrawArrays 和 glDrawElements 的作用都是从一个数据数组中提取数据渲染基本图元。
- GL_POINTS:把每一个顶点作为一个点进行处理,顶点n即定义了点n,共绘制N个点。
- GL_LINES:连接每两个顶点作为一个独立的线段,顶点2n-1和2n之间共定义了n条线段,总共绘制N/2条线段。
- GL_LINE_STRIP:绘制从第一个顶点到最后一个顶点依次相连的一组线段,第n和n+1个顶点定义了线段n,总共绘制n-1条线段。
- GL_LINE_LOOP:绘制从第一个顶点到最后一个顶点依次相连的一组线段,然后最后一个顶点和第一个顶点相连,第n和n+1个顶点定义了线段n,总共绘制n条线段。
- GL_TRIANGLES:把每三个顶点作为一个独立的三角形,顶点3n-2、3n-1和3n定义了第n个三角形,总共绘制N/3个三角形。
- GL_TRIANGLE_STRIP:绘制一组相连的三角形,对于奇数n,顶点n、n+1和n+2定义了第n个三角形;对于偶数n,顶点n+1、n和n+2定义了第n个三角形,总共绘制N-2个三角形。
- GL_TRIANGLE_FAN:绘制一组相连的三角形,三角形是由第一个顶点及其后给定的顶点确定,顶点1、n+1和n+2定义了第n个三角形,总共绘制N-2个三角形。
其中:
GL_TRIANGLES:V0V1V2, V3V4V5, V6V7V8……
GL_TRIANGLE_FAN:V0V1V2, V0V2V3, V0V3V4……
GL_TRIANGLE_STRIP:V0V1V2, V1V2V3, V2V3V4……
2.1 glDrawArrays
The glDrawArrays function specifies multiple primitives to render.
void WINAPI glDrawArrays(
GLenum mode,
GLint first,
GLsizei count
);
mode:
GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_QUAD_STRIP, GL_QUADS, and GL_POLYGON.
first:
The starting index in the enabled arrays.
count:
The number of indexes to render.
2.2 glDrawElements
The glDrawElements function renders primitives from array data.
The glDrawElements function is only available in OpenGL version 1.1 or later.
void WINAPI glDrawElements(
GLenum mode,
GLsizei count,
GLenum type,
const GLvoid *indices
);
mode:
The kind of primitives to render. It can assume one of the following symbolic values: GL_POINTS, GL_LINE_STRIP, GL_LINE_LOOP, GL_LINES, GL_TRIANGLE_STRIP, GL_TRIANGLE_FAN, GL_TRIANGLES, GL_QUAD_STRIP, GL_QUADS, and GL_POLYGON.
count:
The number of elements to be rendered.
type:
The type of the values in indices. Must be one of GL_UNSIGNED_BYTE, GL_UNSIGNED_SHORT, or GL_UNSIGNED_INT.
indices:
A pointer to the location where the indices are stored.
绑定VAO时也会自动绑定EBO。
不要在解绑VAO之前解绑EBO(GL_ELEMENT_ARRAY_BUFFER)。
3、代码实现
#pragma once
#include "Point3d.h"
#include #include "EarthGrid3d.h"
EarthGrid3d::EarthGrid3d()
{
_uStepsNum = 120;
_vStepNum = 120;
}
void EarthGrid3d::generalSphereGrid()
{
double ustep = 1 / (double)_uStepsNum, vstep = 1 / (double)_vStepNum;
int np = 0;
int nf = 0;
_verticesNum = (_vStepNum*_uStepsNum + 1)*(3 + 2);
_verticesArr = new float[_verticesNum];
_indicesNum = (_uStepsNum * 2 + _uStepsNum * 2 * (_vStepNum - 2)) * 3;
_indicesArr = new int[_indicesNum];
//
// 北极的一个点
{
Point3d pt0 = getSpherePoint(0, 0);
_verticesArr[5 * np] = pt0.x;
_verticesArr[5 * np + 1] = pt0.y;
_verticesArr[5 * np + 2] = pt0.z;
_verticesArr[5 * np + 3] = 0.5;
_verticesArr[5 * np + 4] = 0;
np++;
}
// 中间的点
for (int j = 1; j < _vStepNum; j++) //v-1个点(共v+1个点)
{
for (int i = 0; i <= _uStepsNum; i++) //u+1个点 (共u+1个点)
{
Point3d pt = getSpherePoint(ustep*i, vstep*j);
_verticesArr[5 * np] = pt.x;
_verticesArr[5 * np + 1] = pt.y;
_verticesArr[5 * np + 2] = pt.z;
_verticesArr[5 * np + 3] = 1 - ustep * i;
_verticesArr[5 * np + 4] = vstep * j;
np++;
}
}
// 南极的一个点
{
Point3d pt1 = getSpherePoint(1, 1);
_verticesArr[5 * np] = pt1.x;
_verticesArr[5 * np + 1] = pt1.y;
_verticesArr[5 * np + 2] = pt1.z;
_verticesArr[5 * np + 3] = 0.5;
_verticesArr[5 * np + 4] = 1;
//np++;
}
//
// 上下2行的三角形组
for (int i = 0; i < _uStepsNum; i++) {
//第一层u个三角形
_indicesArr[nf++] = 0;
_indicesArr[nf++] = 1 + i;
_indicesArr[nf++] = 2 + i;
//最后一层u个三角形
_indicesArr[nf++] = np - 1;
_indicesArr[nf++] = np - 2 - i;
_indicesArr[nf++] = np - 3 - i;
}
// 中间的v-2行的三角形组
for (int j = 0; j < _vStepNum - 2; j++) { //共v-2行
for (int i = 0; i < _uStepsNum; i++) { //共u列
/*
* |\
* | \
* |__\
*/
_indicesArr[nf++] = (_uStepsNum + 1)*j + 1 + i;
_indicesArr[nf++] = (_uStepsNum + 1)*(j + 1) + 1 + i;
_indicesArr[nf++] = (_uStepsNum + 1)*(j + 1) + 2 + i;
/*
* __
* \ |
* \ |
* \|
*/
_indicesArr[nf++] = (_uStepsNum + 1)*j + 1 + i;
_indicesArr[nf++] = (_uStepsNum + 1)*(j + 1) + 2 + i;
_indicesArr[nf++] = (_uStepsNum + 1)*j + 2 + i;
}
}
}
void EarthGrid3d::generalSphereLines()
{
double ustep = 1 / (double)_uStepsNum, vstep = 1 / (double)_vStepNum;
int np = 0;
_linesNum = (_vStepNum*_uStepsNum)*6;
_linesArr = new float[_linesNum];
// 绘制24条经线
for (int i = 0; i < _uStepsNum; i+= _uStepsNum/24)
{
for (int j = 0; j < _vStepNum; j++)
{
Point3d pt = getSpherePoint(ustep*i, vstep*j, 1.01f);
_linesArr[3 * np] = pt.x;
_linesArr[3 * np + 1] = pt.y;
_linesArr[3 * np + 2] = pt.z;
np++;
Point3d pt2 = getSpherePoint(ustep*i, vstep*(j+1), 1.01f);
_linesArr[3 * np] = pt2.x;
_linesArr[3 * np + 1] = pt2.y;
_linesArr[3 * np + 2] = pt2.z;
np++;
}
}
// 绘制1条纬线(赤道)
for (int i = 0; i < _uStepsNum; i++)
{
int j = _vStepNum / 2;
//for (int j = 0; j < _vStepNum; j++)
{
Point3d pt = getSpherePoint(ustep*i, vstep*j, 1.01f);
_linesArr[3 * np] = pt.x;
_linesArr[3 * np + 1] = pt.y;
_linesArr[3 * np + 2] = pt.z;
np++;
Point3d pt2 = getSpherePoint(ustep*(i+1), vstep*j, 1.01f);
_linesArr[3 * np] = pt2.x;
_linesArr[3 * np + 1] = pt2.y;
_linesArr[3 * np + 2] = pt2.z;
np++;
}
}
}
4、运行结果(整体地球)
4.1 opengl / glut / c++ (3d)
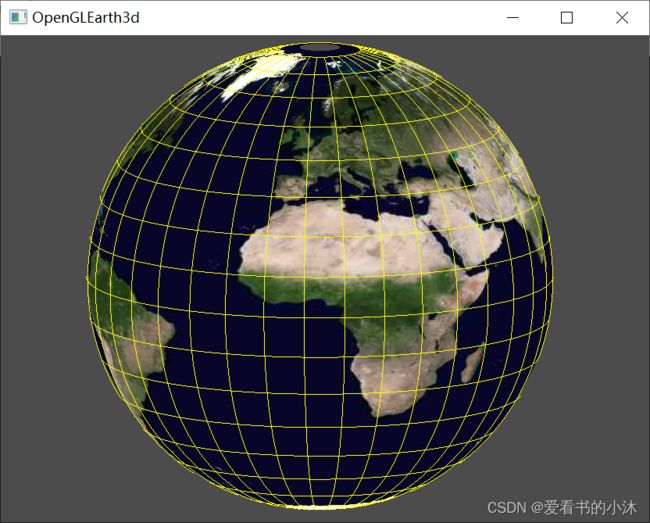
4.2 opengl / glfw / glad / stb_image / c++ (3d)
4.3 opengl / glfw / glad / stb_image /c++ (3d,天空盒,高度贴图)
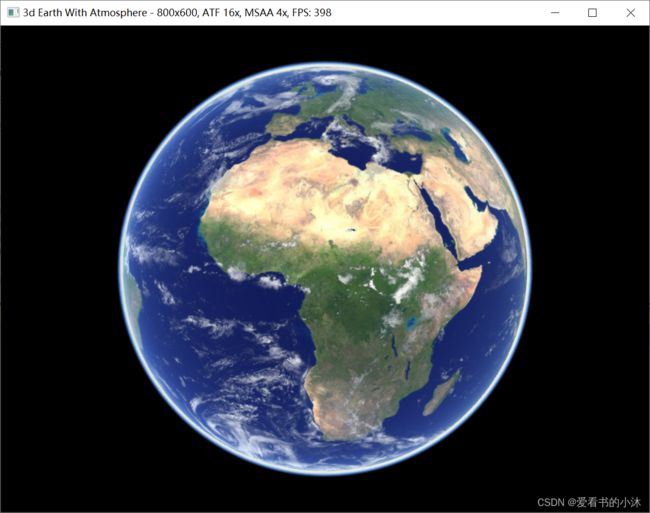
4.4 opengl / win32/ glew / FreeImage / c++ (3d,大气层)
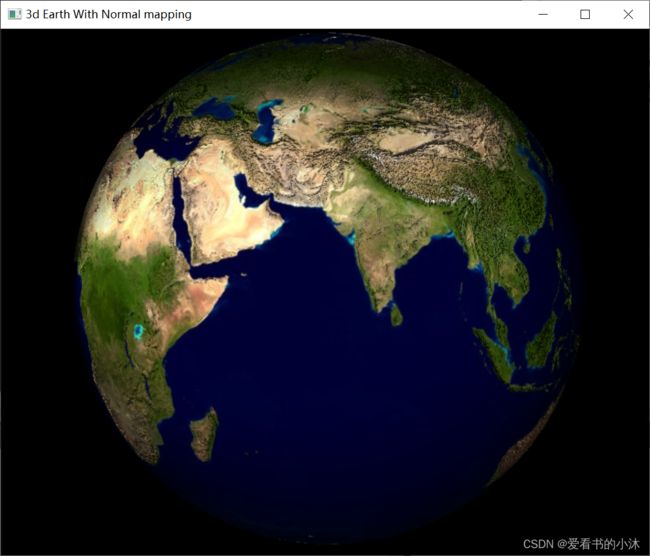
4.5 opengl / freeglut / glew / FreeImage / c++ (3d,法线贴图)
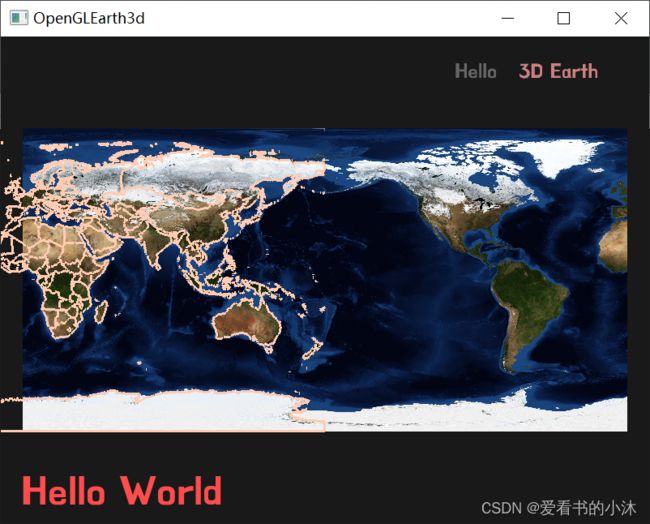
4.6 opengl / glfw / glad / stb_image / freetype / c++ (2d/3d,加载geojson)
4.7 opengl / glfw / glad / FreeImage / c++ (3d,白天层/黑夜层/云层)
5、运行结果(瓦片地球)
5.1 opengl / sdl / boost::asio / c++ (2d,瓦片贴图)
5.2 opengl / glfw / glew / curl / proj4 / gdal / stb_image / c++ (3d,瓦片贴图)
-
加载卫星影像图
-
加载行政地图
-
加载shp(shapefile)文件和显示:
-
绘制自定义的图形元素(线、面等)
-
切换地球底图的瓦片图源
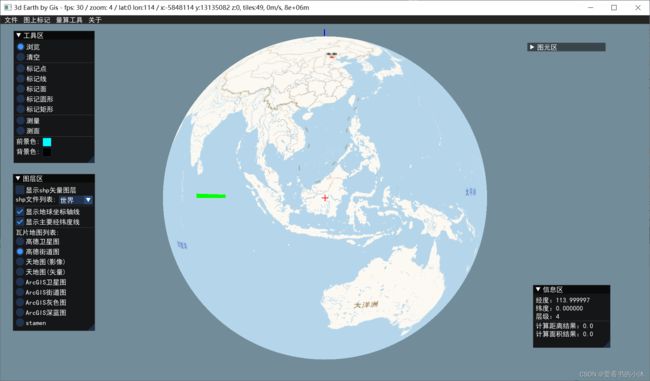
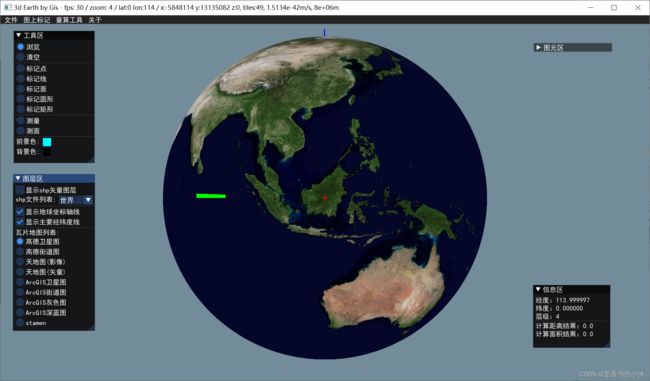
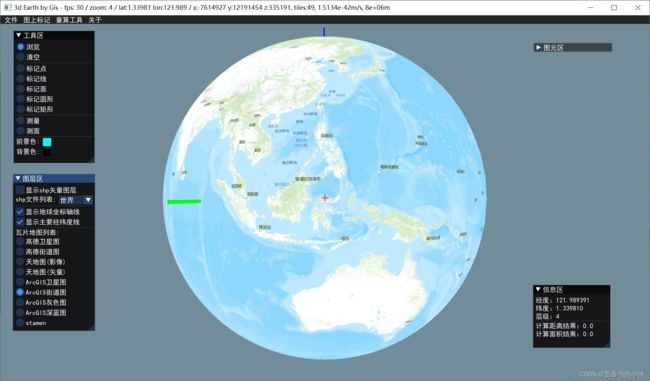
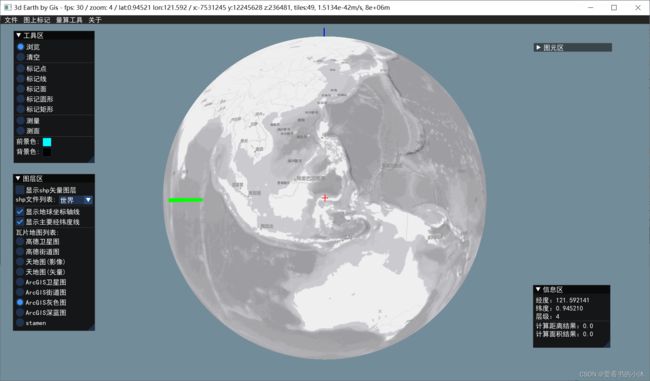
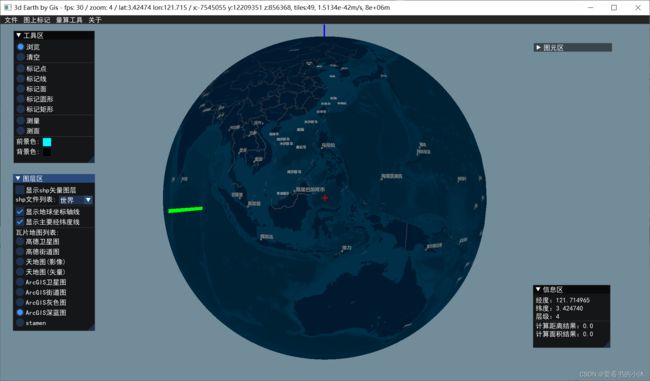
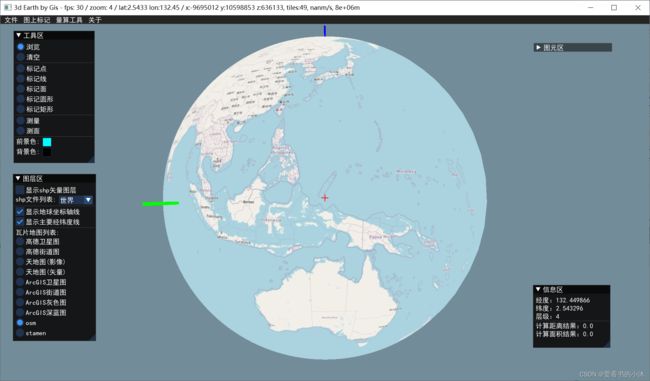
5.3 opengl / glfw / glad / boost::asio / proj4 / stb_image / c++ (3d,瓦片贴图)

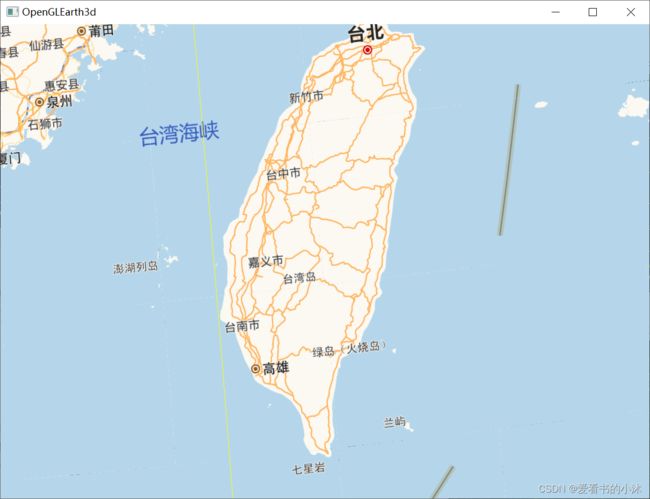
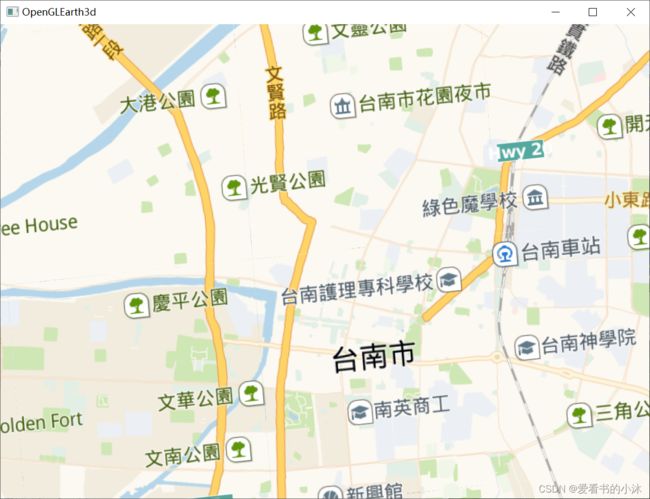
结语
如果您觉得该方法或代码有一点点用处,可以给作者点个赞,或打赏杯咖啡;╮( ̄▽ ̄)╭
如果您感觉方法或代码不咋地//(ㄒoㄒ)//,就在评论处留言,作者继续改进;o_O???
如果您需要相关功能的代码定制化开发,可以留言私信作者;(✿◡‿◡)
感谢各位童鞋们的支持!( ´ ▽´ )ノ ( ´ ▽´)っ!!!
![]()