基于LMS算法的Mackey Glass时间序列预测（Matlab代码实现）

 ‍个人主页：研学社的博客 

欢迎来到本博客❤️❤️

博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

本文目录如下：

目录

1 概述

2 运行结果

3 Matlab代码实现

4 参考文献

---

1 概述

时间序列预测方法是科学、经济、工程等领域的研究重点之一。经典的时间序列预测方法在用于非线性系统预测时有一定的困难,而神经网络具有较好的非线性特性,为时间序列预测开辟了新的途径。但神经网络具有易陷入局部极小值以及全局搜索能力弱等缺点;而遗传算法具有较好的全局最优搜索能力,遗传神经网络将两者结合,既保留了遗传算法的全局寻优的特点,又兼有神经网络的非线性特性和收敛的快速性。Mackey-Glass(MG)混沌时间序列具有非线性特性,是时间序列预测问题中的基准问题之一,具有代表性。

时滞混沌系统即具有混沌运动的时滞系统。时滞系统是系统中一处或几处的信号传递有时间延迟的系统。所谓混沌是指具有以下特点的一类现象：由确定性产生；具有有界性；具有非周期性；初始条件具有极端敏感性。

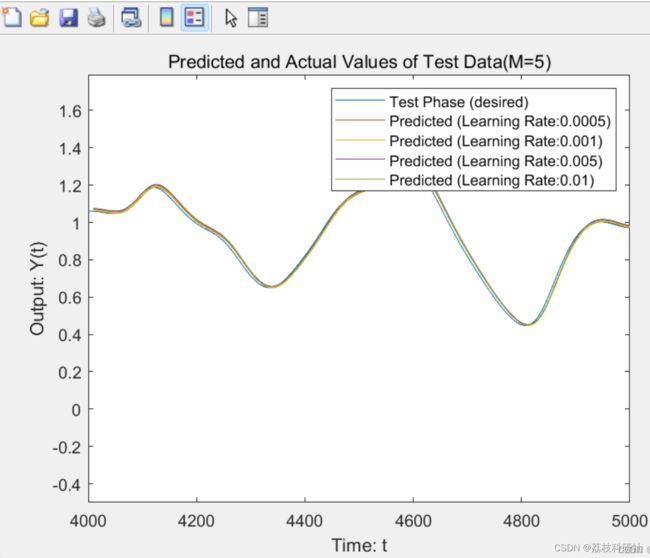
2 运行结果

 

 

 

部分代码：

clc
clear all
close all

%% Load Mackey Glass Time series data
load Dataset\Data.mat 

%% Training and Testing datasets
% For training
Tr=1:4000;    % First 4000 samples for training
Xr(Tr)=Data(Tr);      % Selecting a chuck of series data x(t)
% For testing
Ts=4000:5000;   % Last 1000 samples for testing
Xs(Ts)=Data(Ts);      % Selecting a chuck of series data x(t)

%% LMS Parameters
% We run the LMS algorithm for different learning rates
etaValues = [5e-4 1e-3 5e-3 0.01]; % Learning rate
M=5;    % Order of LMS filter
W_init=randn(M+1,1); % Initialize weights

figure(2)
plot(Tr(2*M:end-M),Xr(Tr(2*M:end-M)));      % Actual values of mackey glass series

figure(3)
plot(Ts,Xs(Ts));        % Actual unseen data

for eta = etaValues
      
    U=zeros(1,M+1); % Initialize values of taps
    W=W_init; % Initialize weights
    E=[];         % Initialize squared error vector
    
    %% Learning weights of LMS (Training)
    for i=Tr(1):Tr(end)-1
        U(1:end-1)=U(2:end);    % Shifting of tap window
        U(end)=Xr(i);           % Input (past/current samples)
        
        Y(i)=W'*U';             % Predicted output
        e(i)=Xr(i+1)-Y(i);        % Error in predicted output

        W=W+eta*e(i)*U';     % Weight update rule of LMS

        E(i)=e(i).^2;   % Concatenate current squared error
    end

    %% Prediction of a next outcome of series using previous samples (Testing)
    for i=Ts(1):Ts(end)
        U(1:end-1)=U(2:end);    % Shifting of tap window
        U(end)=Xs(i);           % Input (past/current samples)

        Y(i)=W'*U';             % Calculating output (future value)
        e(i)=Xs(i)-Y(i);        % Error in predicted output

        E(i)=e(i).^2;   % Current mean squared error (MSE)
    end
    
    % Plot the squared error over the training sample iterations
    figure(1),hold on;
    plot(Tr(1:end-1),E(:,Tr(1:end-1)));   % MSE curve
    hold off;
    
    % Plot the predicted training data
    figure(2), hold on;
    plot(Tr(2*M:end-M),Y(Tr(2*M:end-M))')   % Predicted values during training
    hold off;

%   Comment out the following parts to plot prediction of the test data    
    figure(3), hold on; 
    plot(Ts(2*M:end),Y(Ts(2*M:end))');  % Predicted values of mackey glass series (testing)
    hold off;
    
    MSEtr= mean(E(Tr));  % MSE of training
    MSEts= mean(E(Ts));  % MSE of testing

    disp(['MSE for test samples (Learning Rate: ' num2str(eta) '):' num2str(MSEts)]);
    
end

3 Matlab代码实现

4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]邵海见,邓星.基于RBF神经网络结构选择方法的Mackey-Glass与Lorenz混沌时间序列预测建模[J].江苏科技大学学报(自然科学版),2018,32(05):701-706.