ISODATA分类法

                                                             ISODATA分类法介绍

作者：liangdas

出处：简单点儿，通俗点儿，机器学习      http://blog.csdn.net/liangdas/article/details/39805815

引言：

       上一篇K-Means分类方法，但它一个重要的缺点：分类的类别数目事先必须确定下来，而作为非监督分类，事先我们很难去确定待分类的集合（样本）中到底有多少类别，基于这一缺点，后来人们在K-Means的基础上做了改进，提出了另外一种非监督分类方法：迭代自组织数据分析算法（ISODATA），它在K-均值算法的基础上，对分类过程增加了“合并”和“分裂”两个操作，并通过设定参数来控制这两个操作的一种聚类算法。

基本原理：

       对于目标函数，ISODATA的目标函数和K-Means的目标函数是一样的，都是：
         

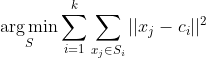
       其中k最后得到的类别个数，S是分类的类别集合 ，x_j是属于S_i类的每一个样本，C_i是S_i的类别中心。

       ISODATA的聚类的类别数目随着聚类的进行，是变化着的，因为在聚类的过程中，对类别数有一个“合并”和“分裂”的操作。合并是当聚类结果某一类中样本数太少，或两个类间的距离太近时，将这两个类别合并成一个类别；分裂是当聚类结果中某一类的类内方差太大，将该类进行分裂，分裂成两个类别。

ISODATA分类的过程和K-Means一样，用的也是迭代的思想：先随意给定初始的类别中心，然后做聚类，通过迭代，不断调整这些类别中心，直到得到最好的聚类中心为止。

初始参数：

    ISODATA有7个初始变量: 6个初始参数（K，k，θN，θc，θs，L，I）。

    K: 期望得到的聚类数；

    k: 初始的设定的聚类数；

    θN: 每一个类别中最少的样本数，若少于此数则去掉该类别；

    θs: 一个类别中，样本特征中最大标准差。若大于这个值，则可能分裂；

    θc: 两个类别中心间的最小距离，若小于此数，把两个类别需进行合并；

    L: 在一次合并操作中，可以合并的类别的最多对数；

    I: 迭代运算的次数。

其算法步骤如下^[1][2][3][4]：

（1） 初始值设定。

        取K个中心C₁, C₂…C_k作为聚类中心，同时设定上述的7个初始参数；

（2）用最小距离法对全体样本进行聚类。

        依据下列关系将每个样本x分到聚类中心为C_i的聚类块S_i中。

        若 d_j = mind(x, C_i)，则x∈S_j。

（3）去掉那些类别中样本数小于N的类别。

        若有任何一个类别Si满足N_ii是聚类块S_i的样本数，则舍去类别S_i，并令k=k-1；同时跳到步骤（2），也就是重新对全体样本进行聚类。

（4）更新聚类中心。

        按照下式更新聚类中心：          

         

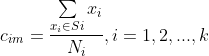
        m是特征（属性），C_im表示第i个类别的第m维特征，x_i是属于类别S_i的样本

（5）计算每个类的类内平均距离。

       

        第i个类别中的所有样本到其类别中心C_i的距离为：

计算所有类的总体平均距离。

         

        计算所有样本到其相应聚类中心的平均距离：

（6）判断停止、分裂或合并。

        若迭代次数I = NS，则算法结束；

        若k <= K/2，则转到（7）（将一些类分裂）；

        若k >= 2K，则转至（8）（跳过分裂处理）；

        若K/2 < k < 2K，当迭代次数I是奇数时转至（7）（分裂处理）；迭代次数I是偶数时转至(8)（合并处理）。这里通过奇数偶数来判断，

（7）分裂操作

        求每个类别中每个分量（也叫每一维特征）的标准差

        对每一个聚类S_i，用下列公式求标准差，

         

        式中x_lm是S_i类中的第l(英文小写字母，和L相对)个样本的第m个分量，C_im是类别S_i的第m个分量的值；δ_im是类别S_i的第m个分量的标准差，m是样本的维数， N_i是属于S_i类别中的样本。

        找到每类分量（特征维）中标准偏差最大的值:

       

        若对任一个，存在,同时有满足以下两个条件之一:

        Ø        且，即S_i类的类内平均距离大于所有类的总体平均距离，而且S_i类的中的样本数N_i超过类内最小样本数θN的一倍以上。

        Ø        即当前类别数k是期望类别数的一半以下。

        则把类别S_i分裂维两个聚类块，其中心对应为C_i⁺和C_i^-，把原来的C_i取消，且令k＝k+1。C_i⁺和C_i^-的计算方法如下：

        给定一个h值，使0，其中h值的选择要使得S_i类中的点到C_i⁺和C_i^-的距离不同，但由要保证以前在S_i中的样本仍在这两个新的集合中。

        如果本步骤完成了分裂操作,则转到步骤2, 否则继续。

（8）合并操作

        (1)对于所有的聚类中心，计算两两之间的距离：

       

        (2)比较D_ij和θ_c，把小于θ_c的D_ij按大小作升序排列，

        (3)从最小的D_ij开始，对于每个D_ij合并两类C_i和C_j，聚类中心为：

       

        并把聚类中心数减少，k＝k－1。

        (4)从第二个D_ij开始，首先要检查其涉及的类别C_i和C_j是否已在前面合并过程中被合并过，如两者都未被合并，则执行合并过程，直到整个合并的类别对数到达L个，则合并操作结束。

（9）结束操作

        若这是最后一次迭代，这程序结束，否则可根据需要转到步骤1或步骤2，如果需由操作者改变输入参数，则转步骤1；如果输入参数不变，则转到步骤2，同时，迭代计数器要加1，即i＝i＋1。

实例解释：

       用前面K-Means测试实例的数据，初始设置为：

       期望得到的聚类数K为4，初始聚类中心k有5个，分别是(62,372)，(62，372)，(2,273)，(-76,483)，(24,326)，(326,244)；

       每一个类别中最少的样本数θN为100；

     一个类别中，样本特征中最大标准差θs也为100。只有大于这个值，则可能分裂；

       两个类别中心间的最小距离θc为200；

       在一次合并操作中，可以合并的类别的最多对数L为2；

       迭代运算的次数I为11。

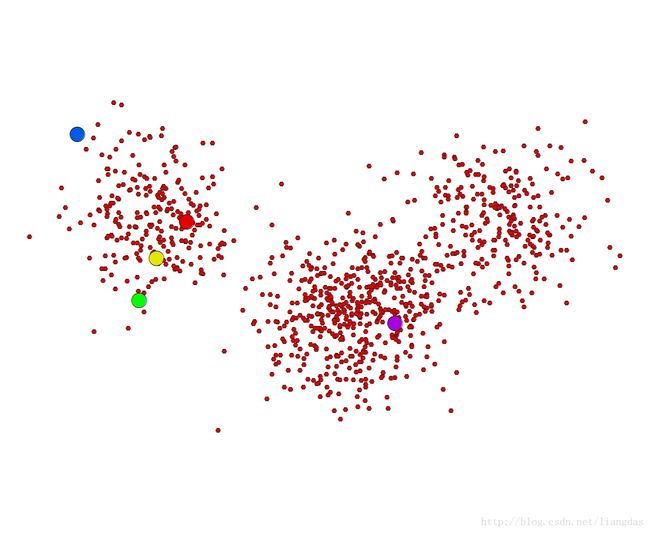
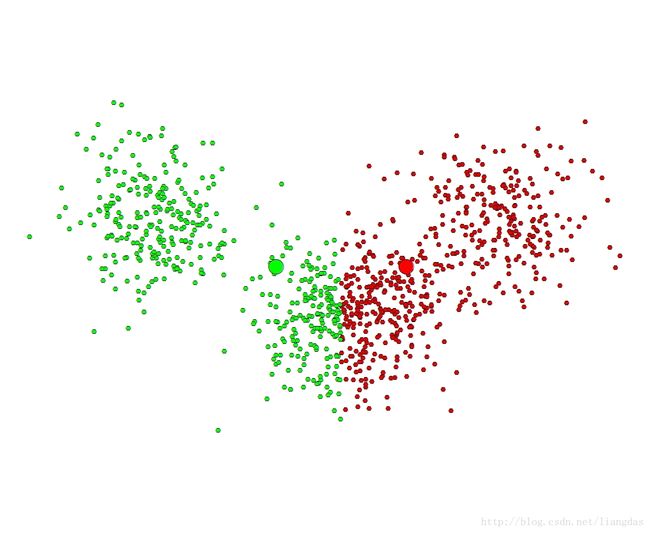
       下面一系列图的用ISODATA聚类过程的迭代图：

                 

                                      图1 初始状态                                                                                   图2 第一次迭代
             

                                 图3 第二次迭代                                                                                 图4 第三次迭代

                 

                           图5 第四次迭代                                                                                   图6 第五次迭代

                  

                                图7 第六次迭代                                                                                  图8 第七次迭代

                  

                            图9 第八次迭代                                                                               图10 第九次迭代

                  

                                  图11 第十次迭代                                                                             图12 第十一次迭代

       从图中可以看出，在第八次迭代之后，聚类就已经收敛了，从第八次到第十一次迭代，聚类的状态就已经不再发生变化啦。

       从原始数据直观可以看出，这个数据最好的分类中心是三个，即使初始设置的类别中心为5类，但是经过ISODATA聚类之后，还是能得到客观上所看到的三个类别中心。而如果是K-Means分类法，如果我们设置初始类别中心为5的话，最后得到的一定也是5类，和客观类别中心不符合。

ISODATA优缺点：

        ISODATA 可以在聚类过程中自动调整类别个数和类别中心，使聚类结果能更加靠近客观真实的聚类结果。        

       ISODATA算法需要设置的参数比较多，参数值不好确定。不同的参数之间相互影响，而且参数的值和聚类的样本集合也有关系，要得到好的聚类结果，需要有好的初始设置值，可以通过多次设置不同的值进行不同的实验，然后取一些已知的样本来检验聚类结果的精度，以最后取得更好的分类结果的那次实验为准；或者考虑和其他方法相结合来得到更好的分类结果。

参考资料：

[1]百度百科- (ISODATA算法)

http://wenku.baidu.com/view/c8ff7c3987c24028915fc37b.html

[2]百度文库-第二章(ISODATA算法实例)

http://wenku.baidu.com/view/4f2cda4c2b160b4e767fcf70.html

[3]百度文库-ISODATA算法

http://baike.baidu.com/link?url=gqL6wqnLil5FMqiWN7OCdVuWH7sZzxYOGMEfjK2K81blLgImaNmCMDcVjFBswxxitubLX0ltx9M1TZc-p4QPMK

[4]百度文库-ISODATA迭代自组织数据分析流程

http://wenku.baidu.com/link?url=ylYLA8E8Mh6-XYccljV4YW40viFakvPc69nUoifU9Xfn4mfug5kAj3tZvDKL9vsJJMJSxdUtP8I03XCYbK8RZUESvP3hbYUBcicuvtrDwwC

ps：使用或者转载请标明出处，禁止以商业为目的的使用。

如果有需要word版，或者是pdf版的，请与我联系，QQ：358536026