笔记:Delaunay三角剖分(Delaunay Triangulation)相关知识
笔记:Delaunay三角剖分(Delaunay Triangulation)相关知识 http://www.cnblogs.com/soroman/archive/2007/05/17/750430.html
最近接触到计算Delaunay三角剖分的问题,也算是计算几何的一个经典问题了。按照别人的算法,也自己实现了个( 源代码下载),发现点集大的时候,程序计算起来特慢。后来分析发现,别人程序号称的都是O(nlogn)的,我的却成了O(n*n)的,算法都是一样,后来才发现是数据结构的问题,看来程序=算法+数据结构,有道理。闲着,就整理了些相关知识,组织如下:
1.Delaunay三角剖分&Voronoi图定义
2.计算Delaunay三角剖分的算法及分析
3.例子程序&代码
大话
点集的三角剖分(Triangulation),对数值分析(比如有限元分析)以及图形学来说,都是极为重要的一项预处理技术。
尤其是Delaunay三角剖分,由于其独特性,关于点集的很多种几何图都和Delaunay三角剖分相关,如Voronoi图,EMST树,Gabriel图等。Delaunay三角剖分有几个很好的特性:
1.最大化最小角,“最接近于规则化的“的三角网。
2.唯一性(任意四点不能共圆)。
概念及定义
二维实数域(二维平面)上的三角剖分
定义1:假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段, E为e的集合。
那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:
1.除了端点,平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面,且所有三角面的合集就是点集V的凸包。
那什么是Delaunay三角剖分呢?不过是一种特殊的三角剖分罢了。从Delaunay边说起。
Delaunay边
定义2:假设E中的一条边e(两个端点为a,b),e若满足下列条件,则称之为Delaunay边:
存在一个圆经过a,b两点,圆内不含点集V中任何的点,这一特性又称空圆特性。
Delaunay三角剖分
定义3:如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。
我们看几个图:
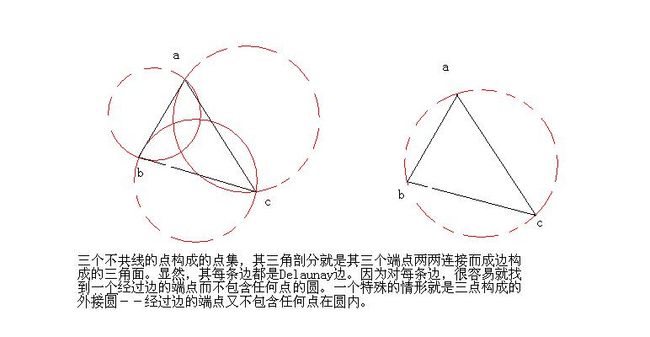


由上面的图引出Delaunay三角剖分的另一种定义:
定义4:假设T为V的任一三角剖分,则T是V的一个Delaunay三角剖分,当前仅当T中的每个三角形的外接圆的内部不包含V中任何的点。
Voronoi图
定义5:V的Voronoi图是由多边形区域的集合(有些区域可能不是闭合的),该区域仅含点集中的一个点v,区域中的任何位置到v的距离都比该位置到点集中其它所有点的距离短。
由Voronoi图和Delaunay三角剖分的关系,可以引出另一个Delaunay三角剖分的定义:
定义6:将Voronoi图相邻区域(共边的区域)中的点连接起来构成的图,称为Delaunay三角剖分。
如下图:

概念部分到此,下面看看怎么求Delaunay三角剖分。
计算Delaunay三角剖分
问题1:计算二维Delaunay三角剖分
问题输入:二维实数域上的点集V
问题输出:Delaunay三角剖分DT = (V, E).
算法
由不同的定义对应有不同的算法。用得较多的是基于定义3或4的算法。
目前常用的算法又分为好几种,被不同的家伙发现。什么扫描线法(Sweepline),随机增量法(Incremental),分治法(Divide and Conquer)啊等等。
随机增量法(Incremental)
其中,随机增量法较为简单,遵循增量法的一贯思路,即按照随机的顺序依次插入点集中的点,在整个过程中都要维护并更新一个与当前点集对应的Delaunay三角剖分。考虑插入vi点的情况,由于前面插入所有的点v1,v2,...,vi-1构成的DT(v1,v2,...,vi-1)已经是Delaunay三角剖分,只需要考虑插入vi点后引起的变化,并作调整使得DT(v1,v2,...,vi-1) U vi成为新的Delaunay三角剖分DT(v1,v2,...,vi)。
(插入调整过程:首先确定vi落在哪个三角形中(或边上),然后将vi与三角形三个顶点连接起来构成三个三角形(或与共边的两个三角形的对顶点连接起来构成四个三角形),由于新生成的边以及原来的边可能不是或不再是Delaunay边,故进行边翻转来调整使之都成为Delaunay边,从而得出DT(v1,v2,...,vi)。)
其Pseudocode如下:
Algorithm IncrementalDelaunay(V)
Input: 由n个点组成的二维点集V
Output: Delaunay三角剖分DT
1.add a appropriate triangle boudingbox to contain V ( such as: we can use triangle abc, a=(0, 3M), b=(-3M,-3M), c=(3M, 0), M=Max({|x1|,|x2|,|x3|,...} U {|y1|,|y2|,|y3|,...}))
2.initialize DT(a,b,c) as triangle abc
3.for i <- 1 to n
do (Insert(DT(a,b,c,v1,v2,...,vi-1), vi))
4.remove the boundingbox and relative triangle which cotains any vertex of triangle abc from DT(a,b,c,v1,v2,...,vn) and return DT(v1,v2,...,vn).
Algorithm Insert(DT(a,b,c,v1,v2,...,vi-1), vi)
1.find the triangle vavbvc which contains vi // FindTriangle()
2.if (vi located at the interior of vavbvc)
3. then add triangle vavbvi, vbvcvi and vcvavi into DT // UpdateDT()
FlipTest(DT, va, vb, vi)
FlipTest(DT, vb, vc, vi)
FlipTest(DT, vc, va, vi)
4.else if (vi located at one edge (E.g. edge vavb) of vavbvc)
5. then add triangle vavivc, vivbvc, vavdvi and vivdvb into DT (here, d is the third vertex of triangle which contains edge vavb) // UpdateDT()
FlipTest(DT, va, vd, vi)
FlipTest(DT, vc, va, vi)
FlipTest(DT, vd, vb, vi)
FlipTest(DT, vb, vc, vi)
6.return DT(a,b,c,v1,v2,...,vi)
Algorithm FlipTest(DT(a,b,c,v1,v2,...,vi), va, vb, vi)
1.find the third vertex (vd) of triangle which contains edge vavb // FindThirdVertex()
2.if(vi is in circumcircle of abd) // InCircle()
3. then remove edge vavb, add new edge vivd into DT // UpdateDT()
FlipTest(DT, va, vd, vi)
FlipTest(DT, vd, vb, vi)
Algorithm InCircle(va, vb, vd, vc)
if | a^b^, c^b^, d^b^| > 0, vd is NOT in the circumcircle of abc // a^坐标为(ax,ay,ax*ax+ay*ay),a^b^为向量
if | a^b^, c^b^, d^b^| == 0, vd is on the circumcircle of abc
if | a^b^, c^b^, d^b^| < 0, vd is in the circumcircle of abc
Note: Details of InCircle():
如下图:

抛物线P (z = x*x + y*y), 现有x-y平面上a,b,c三点,现在要测试点d是否在a,b,c的外接圆内,将a,b,c,d四点lift up,与P相交于a^,b^,c^,d^,则有:
case 1:如果d正好位于外接圆 上,则d^必在由a^,b^,c^三点构成的平面H 上。此刻向量 a^b^, c^b^, d^b^构成的矩阵的行列式 det==0
case 2:如果d位于外接圆 内,即d',则d'^必在由a^,b^,c^三点构成的平面H 下面。即向量 a^b^, c^b^, d^b^构成的矩阵的行列式 det<0
case 3:如果d位于外接圆 外,即d'',则d''^必在由a^,b^,c^三点构成的平面H 上面。即向量 a^b^, c^b^, d^b^构成的矩阵的行列式 det>0
复杂度分析
问题的规模为点集中的点的总个数n(没有重合的点),循环内的基本的操作有:
1.寻找插入点所在的三角形(FindTriangle())
2.测试点是否在外接圆内(InCircle())
3.更新三角网(UpdateDT())
4.寻找共测试边的第三顶点(FindThirdVertex())
考虑最坏情况:
时间复杂度T = T(addboudingbox()) + Sum(T(insert(i), i=1,2,...,n)) + T(removeboundingbox)
因为addboudingbox()和removeboundingbox不随n变化,是个常量。T(addboudingbox()) = O(1), T(removeboundingbox()) = O(1).
T = Sum(T(insert(i), i=1,2,...,n)) + O(1) + O(1).
考虑插入第i个的点的时间:
T(insert(i)) = T(FindTriangle(i)) + T(UpdateDT(i)) + K*T(FlipTest(i)) (K为常数)
故T = Sum(T(FindTriangle(i)), i=1,2,..,n) + Sum(T(UpdateTD(i)), i=1,2,..,n) + K*Sum(T(FlipTest(i)), i=1,2,..,n)
挨个考虑:
FindTriangle(i)是要找出包含第i个点的三角形,由欧拉公式知道,平面图的面数F是O(n), n为顶点数,故此时总的三角形数是O(i)的。所以问题相当于在O(i)个记录中查找目标记录,如果不借助特殊的数据结构,按照一般顺序查找,需要O(i)的时间。
T(FindTriangle(i)) = O(i),故:Sum(T(FindTriangle(i)), i=1,2,..,n) = O(n*n)
UpdateTD(i)是更新三角网数据结构,插入和删除三角形到当前的三角网是个常量操作,因为已经知道插入和删除的位置。
T(UpdateDT(i)) = O(1),故:Sum(T(UpdateTD(i)), i=1,2,..,n) = O(n)
FlipTest(i)比较复杂些,是个递归过程。细分为:T(FlipTest(i)) = T(FindThirdVertex(i)) + T(InCircle(i)) + T(UpdateDT(i)) + 2*T(FlipTest(j))。(这里,用j来区分不同的深度)
因为InCircle(i)是测试点是否在外接圆内,是个常量操作,不随点数变化而变化。故T(InCircle(i)) = O(1), 又T(UpdateDT(i) = O(1)(见上)
FindThirdVertex(i)是查找目标点,在O(i)个记录中查找目标记录,如果不借助特殊的数据结构,按照一般顺序查找需要O(i)的时间。T(FindThirdVertex(i)) = O(i).
剩下的是递归调用FlipTest的过程,不过还好,因为FlipTest的递归深度只有常数级(设为K)。正比于点在三角网中的度数(degree)。故FlipTest(i)最多调用的次数为2*2*,...,2 = K',还是常数。
故T(FlipTest(i)) = O(i) + O(1) + O(1) + K'*(O(i) + O(1) + O(1)) = O(i) + O(1) + O(1) .
Sum(T(FlipTest(i)), i=1,2,..,n) = O(n*n) + O(n) + O(n)
综上,最坏情况下算法总时间复杂度 T = O(n*n) + O(n) + K*(O(n*n) + O(n) + O(n)) + O(1) + O(1) = O(n*n)
其中,关键的操作是FindTriangle()和FindThirdVertex(),都是n*n次的。
在网上很多资料说随机增量法是O(nlogn)的,但是分析下来,却是O(n*n)的。后来看到别人的实现,原来是用的别的数据结构来存储三角网,减少了FindTriangle()和FindThirdVertex()的复杂度。使得某次查找三角形和共边三角形的第三顶点能在O(logn),而非O(n)的时间内实现。这样,总的查找的时间为 O(log1)+O(log2)+,...+O(logn) = O(nlogn)。程序=算法+数据结构,看来一点没错。
比如说用DAG,Quad-edge等,都能达到O(nlogn)的复杂度。
分治法(Divide and Conquer)
据说是现在实际表现最好的。
扫描线法(Sweepline)
有空再看看其算法思路。
例子程序&代码
网上由很多代码关于计算Delaunay的库,如Triangle, Qhull,看的烦,自己写了个,很简陋,基本上就是随机增量法伪代码的直译,还没时间优化。
有空再整理下约束性Delaunay三角剖分相关知识。
to be continued...
1.Delaunay三角剖分&Voronoi图定义
2.计算Delaunay三角剖分的算法及分析
3.例子程序&代码
大话
点集的三角剖分(Triangulation),对数值分析(比如有限元分析)以及图形学来说,都是极为重要的一项预处理技术。
尤其是Delaunay三角剖分,由于其独特性,关于点集的很多种几何图都和Delaunay三角剖分相关,如Voronoi图,EMST树,Gabriel图等。Delaunay三角剖分有几个很好的特性:
1.最大化最小角,“最接近于规则化的“的三角网。
2.唯一性(任意四点不能共圆)。
概念及定义
二维实数域(二维平面)上的三角剖分
定义1:假设V是二维实数域上的有限点集,边e是由点集中的点作为端点构成的封闭线段, E为e的集合。
那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:
1.除了端点,平面图中的边不包含点集中的任何点。
2.没有相交边。
3.平面图中所有的面都是三角面,且所有三角面的合集就是点集V的凸包。
那什么是Delaunay三角剖分呢?不过是一种特殊的三角剖分罢了。从Delaunay边说起。
Delaunay边
定义2:假设E中的一条边e(两个端点为a,b),e若满足下列条件,则称之为Delaunay边:
存在一个圆经过a,b两点,圆内不含点集V中任何的点,这一特性又称空圆特性。
Delaunay三角剖分
定义3:如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。
我们看几个图:



由上面的图引出Delaunay三角剖分的另一种定义:
定义4:假设T为V的任一三角剖分,则T是V的一个Delaunay三角剖分,当前仅当T中的每个三角形的外接圆的内部不包含V中任何的点。
Voronoi图
定义5:V的Voronoi图是由多边形区域的集合(有些区域可能不是闭合的),该区域仅含点集中的一个点v,区域中的任何位置到v的距离都比该位置到点集中其它所有点的距离短。
由Voronoi图和Delaunay三角剖分的关系,可以引出另一个Delaunay三角剖分的定义:
定义6:将Voronoi图相邻区域(共边的区域)中的点连接起来构成的图,称为Delaunay三角剖分。
如下图:
概念部分到此,下面看看怎么求Delaunay三角剖分。
计算Delaunay三角剖分
问题1:计算二维Delaunay三角剖分
问题输入:二维实数域上的点集V
问题输出:Delaunay三角剖分DT = (V, E).
算法
由不同的定义对应有不同的算法。用得较多的是基于定义3或4的算法。
目前常用的算法又分为好几种,被不同的家伙发现。什么扫描线法(Sweepline),随机增量法(Incremental),分治法(Divide and Conquer)啊等等。
随机增量法(Incremental)
其中,随机增量法较为简单,遵循增量法的一贯思路,即按照随机的顺序依次插入点集中的点,在整个过程中都要维护并更新一个与当前点集对应的Delaunay三角剖分。考虑插入vi点的情况,由于前面插入所有的点v1,v2,...,vi-1构成的DT(v1,v2,...,vi-1)已经是Delaunay三角剖分,只需要考虑插入vi点后引起的变化,并作调整使得DT(v1,v2,...,vi-1) U vi成为新的Delaunay三角剖分DT(v1,v2,...,vi)。
(插入调整过程:首先确定vi落在哪个三角形中(或边上),然后将vi与三角形三个顶点连接起来构成三个三角形(或与共边的两个三角形的对顶点连接起来构成四个三角形),由于新生成的边以及原来的边可能不是或不再是Delaunay边,故进行边翻转来调整使之都成为Delaunay边,从而得出DT(v1,v2,...,vi)。)
其Pseudocode如下:
Algorithm IncrementalDelaunay(V)
Input: 由n个点组成的二维点集V
Output: Delaunay三角剖分DT
1.add a appropriate triangle boudingbox to contain V ( such as: we can use triangle abc, a=(0, 3M), b=(-3M,-3M), c=(3M, 0), M=Max({|x1|,|x2|,|x3|,...} U {|y1|,|y2|,|y3|,...}))
2.initialize DT(a,b,c) as triangle abc
3.for i <- 1 to n
do (Insert(DT(a,b,c,v1,v2,...,vi-1), vi))
4.remove the boundingbox and relative triangle which cotains any vertex of triangle abc from DT(a,b,c,v1,v2,...,vn) and return DT(v1,v2,...,vn).
Algorithm Insert(DT(a,b,c,v1,v2,...,vi-1), vi)
1.find the triangle vavbvc which contains vi // FindTriangle()
2.if (vi located at the interior of vavbvc)
3. then add triangle vavbvi, vbvcvi and vcvavi into DT // UpdateDT()
FlipTest(DT, va, vb, vi)
FlipTest(DT, vb, vc, vi)
FlipTest(DT, vc, va, vi)
4.else if (vi located at one edge (E.g. edge vavb) of vavbvc)
5. then add triangle vavivc, vivbvc, vavdvi and vivdvb into DT (here, d is the third vertex of triangle which contains edge vavb) // UpdateDT()
FlipTest(DT, va, vd, vi)
FlipTest(DT, vc, va, vi)
FlipTest(DT, vd, vb, vi)
FlipTest(DT, vb, vc, vi)
6.return DT(a,b,c,v1,v2,...,vi)
Algorithm FlipTest(DT(a,b,c,v1,v2,...,vi), va, vb, vi)
1.find the third vertex (vd) of triangle which contains edge vavb // FindThirdVertex()
2.if(vi is in circumcircle of abd) // InCircle()
3. then remove edge vavb, add new edge vivd into DT // UpdateDT()
FlipTest(DT, va, vd, vi)
FlipTest(DT, vd, vb, vi)
Algorithm InCircle(va, vb, vd, vc)
if | a^b^, c^b^, d^b^| > 0, vd is NOT in the circumcircle of abc // a^坐标为(ax,ay,ax*ax+ay*ay),a^b^为向量
if | a^b^, c^b^, d^b^| == 0, vd is on the circumcircle of abc
if | a^b^, c^b^, d^b^| < 0, vd is in the circumcircle of abc
Note: Details of InCircle():
如下图:

抛物线P (z = x*x + y*y), 现有x-y平面上a,b,c三点,现在要测试点d是否在a,b,c的外接圆内,将a,b,c,d四点lift up,与P相交于a^,b^,c^,d^,则有:
case 1:如果d正好位于外接圆 上,则d^必在由a^,b^,c^三点构成的平面H 上。此刻向量 a^b^, c^b^, d^b^构成的矩阵的行列式 det==0
case 2:如果d位于外接圆 内,即d',则d'^必在由a^,b^,c^三点构成的平面H 下面。即向量 a^b^, c^b^, d^b^构成的矩阵的行列式 det<0
case 3:如果d位于外接圆 外,即d'',则d''^必在由a^,b^,c^三点构成的平面H 上面。即向量 a^b^, c^b^, d^b^构成的矩阵的行列式 det>0
复杂度分析
问题的规模为点集中的点的总个数n(没有重合的点),循环内的基本的操作有:
1.寻找插入点所在的三角形(FindTriangle())
2.测试点是否在外接圆内(InCircle())
3.更新三角网(UpdateDT())
4.寻找共测试边的第三顶点(FindThirdVertex())
考虑最坏情况:
时间复杂度T = T(addboudingbox()) + Sum(T(insert(i), i=1,2,...,n)) + T(removeboundingbox)
因为addboudingbox()和removeboundingbox不随n变化,是个常量。T(addboudingbox()) = O(1), T(removeboundingbox()) = O(1).
T = Sum(T(insert(i), i=1,2,...,n)) + O(1) + O(1).
考虑插入第i个的点的时间:
T(insert(i)) = T(FindTriangle(i)) + T(UpdateDT(i)) + K*T(FlipTest(i)) (K为常数)
故T = Sum(T(FindTriangle(i)), i=1,2,..,n) + Sum(T(UpdateTD(i)), i=1,2,..,n) + K*Sum(T(FlipTest(i)), i=1,2,..,n)
挨个考虑:
FindTriangle(i)是要找出包含第i个点的三角形,由欧拉公式知道,平面图的面数F是O(n), n为顶点数,故此时总的三角形数是O(i)的。所以问题相当于在O(i)个记录中查找目标记录,如果不借助特殊的数据结构,按照一般顺序查找,需要O(i)的时间。
T(FindTriangle(i)) = O(i),故:Sum(T(FindTriangle(i)), i=1,2,..,n) = O(n*n)
UpdateTD(i)是更新三角网数据结构,插入和删除三角形到当前的三角网是个常量操作,因为已经知道插入和删除的位置。
T(UpdateDT(i)) = O(1),故:Sum(T(UpdateTD(i)), i=1,2,..,n) = O(n)
FlipTest(i)比较复杂些,是个递归过程。细分为:T(FlipTest(i)) = T(FindThirdVertex(i)) + T(InCircle(i)) + T(UpdateDT(i)) + 2*T(FlipTest(j))。(这里,用j来区分不同的深度)
因为InCircle(i)是测试点是否在外接圆内,是个常量操作,不随点数变化而变化。故T(InCircle(i)) = O(1), 又T(UpdateDT(i) = O(1)(见上)
FindThirdVertex(i)是查找目标点,在O(i)个记录中查找目标记录,如果不借助特殊的数据结构,按照一般顺序查找需要O(i)的时间。T(FindThirdVertex(i)) = O(i).
剩下的是递归调用FlipTest的过程,不过还好,因为FlipTest的递归深度只有常数级(设为K)。正比于点在三角网中的度数(degree)。故FlipTest(i)最多调用的次数为2*2*,...,2 = K',还是常数。
故T(FlipTest(i)) = O(i) + O(1) + O(1) + K'*(O(i) + O(1) + O(1)) = O(i) + O(1) + O(1) .
Sum(T(FlipTest(i)), i=1,2,..,n) = O(n*n) + O(n) + O(n)
综上,最坏情况下算法总时间复杂度 T = O(n*n) + O(n) + K*(O(n*n) + O(n) + O(n)) + O(1) + O(1) = O(n*n)
其中,关键的操作是FindTriangle()和FindThirdVertex(),都是n*n次的。
在网上很多资料说随机增量法是O(nlogn)的,但是分析下来,却是O(n*n)的。后来看到别人的实现,原来是用的别的数据结构来存储三角网,减少了FindTriangle()和FindThirdVertex()的复杂度。使得某次查找三角形和共边三角形的第三顶点能在O(logn),而非O(n)的时间内实现。这样,总的查找的时间为 O(log1)+O(log2)+,...+O(logn) = O(nlogn)。程序=算法+数据结构,看来一点没错。
比如说用DAG,Quad-edge等,都能达到O(nlogn)的复杂度。
分治法(Divide and Conquer)
据说是现在实际表现最好的。
扫描线法(Sweepline)
有空再看看其算法思路。
例子程序&代码
网上由很多代码关于计算Delaunay的库,如Triangle, Qhull,看的烦,自己写了个,很简陋,基本上就是随机增量法伪代码的直译,还没时间优化。
有空再整理下约束性Delaunay三角剖分相关知识。
to be continued...