python学习笔记：numpy库，使用matpotlib库绘图
目录
一.Numpy库
1.什么是numpy?
2.Numpy数组和原生Python array数组之间的区别
3.Numpy数组
编辑 4.numpy数组的运算
5.numpy的索引，切片
二.matplotlib
1.绘制直线
2.绘制曲线
3.散点图绘制
4.多界面绘制
5.柱形图绘制
6.3D图形绘制
一.Numpy库
1.什么是numpy?
numpy是python进行科学计算的一个基础软件包，他是一个python库，提供多维数组对象，各种派生对象（如掩码数组和矩阵），以及用于数组快速操作的各种API，包括数学，逻辑，形状操作，排序，选择，输入输出，离散傅里叶变化，基本线性代数，基本统计运算和随机模拟等。
2.Numpy数组和原生Python array数组之间的区别
1.Numpy数组在创建时具有固定的大小，与python的原生数组对象可以动态增长不同，更改其大小将会创建一个新的数组并删除原来的数组。
2.Numpy数组中的元素都需要具有相同的数据类型，因此在内存中的大小相同。
3.Numpy数组有助于对大量数据进行高级教学和其他类型的操作，执行效率高
3.Numpy数组
假如我们现在有两个数组，我们要将两个数组对应位置的值相乘，在c语言中我们需要用到循环来解决，而使用numpy数组那我们可以直接将两个数组进行乘法运算，只需要一行代码即可。
轴：
Numpy的主要对象是同构多维数组，它是一个元素表，所有类型都相同，由非负整数元组索引，在Numpy维度中称为轴。
比如：
数组【1，2，1】：有一个轴，该轴有三个元素1，2，1，轴长为3，这里一轴表示一维数组
数组【【1，0，0】，【0，1，2】】：有两个轴，一轴长度为2，二轴长度为3，这里表示二维数组。
ndarray对象属性如下：
1.ndarray.ndim-数组的轴（维度）的个数
2.ndarray.shape--数组的维度，若有n行，m列则输出为（n,m）
3.ndarray.size--数组元素的总数
4.ndarray.dtype--一个描述数组中元素类型的对象，可以使用标准的python类型创建或指定dtype.
5.ndarray.itemsize--数组中每个元素的字节大小
6.reshape
来看一段代码了解把：
import numpy as np
# 同构生成numpy的一维数组
a = np.arange(1, 10, 2)
print(a)
# shape打印numpy数组的形状
print(a.shape)
# ndim打印numpy数组的轴数
print(a.ndim)
# numpy数组元素的访问，数组名【下标】
print(a[0])
(1).array方法，将一个列表所有元素同构成一个数组
list1 = [1, 2, 3, 4, 5, 6, 7, 8, 9]
a = np.array(list1)
print(a)
print(a.shape)
(2)array方法，将一个列表所有元素同构成一个二维数组
list2 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
b = np.array(list2)
print(b.shape)
(3) reshape():改变数组的维度等形状
a = np.arange(1, 21, 1).reshape(4, 5)
print(a)
print(a.shape) 
还有许多其他的属性，接下来我贴一张图来总结展示就不过多赘述了：
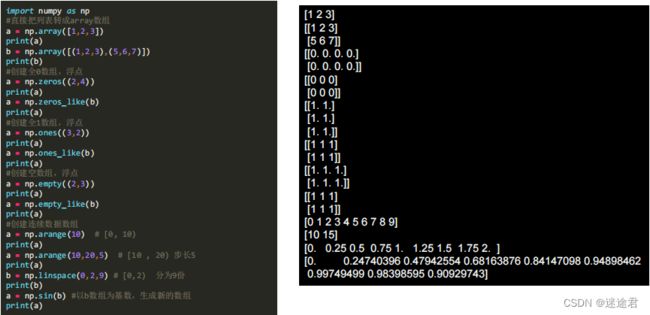4.numpy数组的运算
numpy的运算我用下面一段代码来进行总结，注意没有除法运算
import numpy as np
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
# 乘法运算，将二维数组（矩阵）对应元素相乘
c = a * b
print(c)
# 加法运算，将二维数组（矩阵）对应元素相加
c = a + b
print(c)
# 减法运算
c = a - b
print(c)
print(a.sum())
print(a.max())
print(a.min())
print(a)
# sum(axis=1):将矩阵中各行的所有元素相加作为新元素
print(a.sum(axis=1))
# sum(axis=1):将矩阵中各列元素相加作为新元素
print(a.sum(axis=0)) 
5.numpy的索引，切片
numpy每个轴都会有自己的索引
1.元素访问【第一轴索引，第二轴索引，......】
2.元素的切片 【start: stop: step, start:stop:step,.....】
左闭右开 eg： b[1: 3, 2: 4]
import numpy as np
a = np.arange(10)
print(a.shape)
print(a)
print(a[0], a[-1], a[a.size-1]) # -1表示最后1位
print(a[1: 5]) # 1-5,步长为1 左闭右开
print(a[1:: 2]) # 1-末尾 ，步长为2，左闭右开
二维数组切片：
b = np.arange(20).reshape(4, 5)
print(b)
print(b.shape)
print(b[1][1], b[1][1: -1])
print(b[1, 1], b[1, 1: -1])
print(b[1: 3, 2: 4])
三维数组的切片：
c = np.arange(24).reshape(4, 3, 2)
print(c)
print(c[0: 2, 0: 2, 0: 1])
二.matplotlib
matplotlib是python2D绘图领域使用最广泛的套件，它能让使用者很轻松将数据图形化，并且提供多样化的输出格式，在绘图结构中，figure创建窗口，subplot创建子图，所有的绘图只能在子图上进行，plt表示当前子图，若没有就创建一个子图。
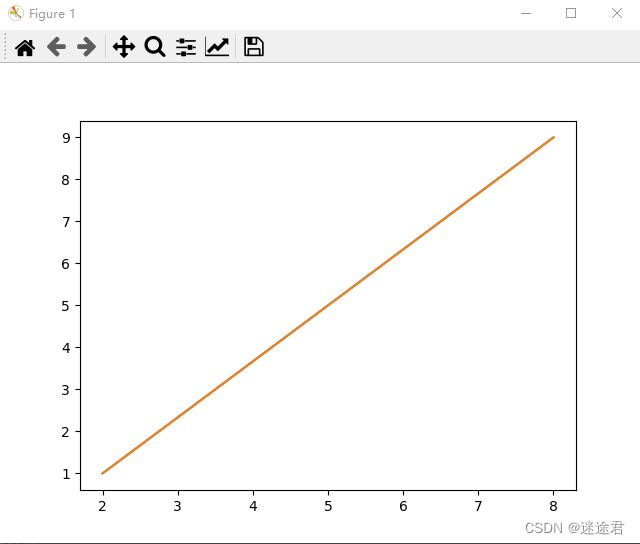
1.绘制直线
我们只需要将两点的x,y坐标进行同构成为两个一维数组，通过plot方法就可以实现，也可以改变参数来修改直线的颜色
import numpy as np
import matplotlib.pyplot as plt
"""
1.绘制直线，直线两点为（2， 1） （8， 9）
"""
x = np.array([2, 8]) # 将两点的x轴坐标，同构成一个一维数组
y = np.array([1, 9]) # 将两点的y轴坐标，同构成一个一维数组
# 绘制直线
plt.plot(x, y)
# plt.plot(x, y, scalex=5, scaley=3)
# 显示窗口
plt.show()
2.绘制曲线
使用arange方法生成0-4Π之间的x坐标，均匀分布步长为0.1，y左边则按正弦函数进行分布
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 4 * np.pi, 0.1) # 0-4Π之间，均匀分配，步长0.1
y = np.sin(x) # 呈正弦变化
plt.plot(x, y)
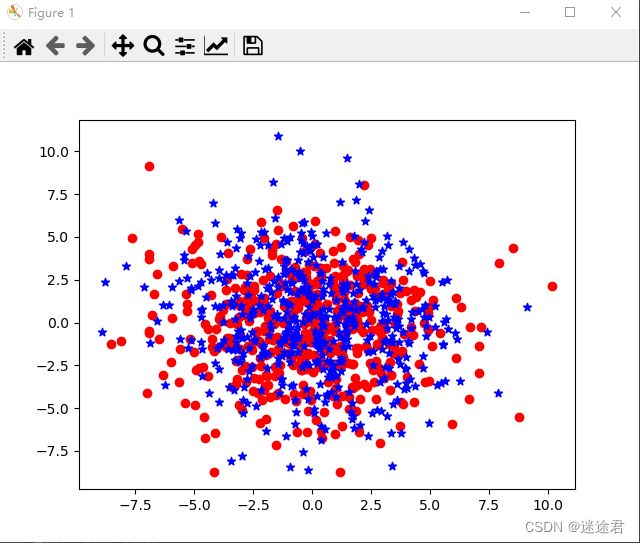
plt.show()
3.散点图绘制
散点图绘制,主要在绘制坐标点的基础上，通过控制坐标点的分布来控制散点图的分布情况
import numpy as np
import matplotlib.pyplot as plt
"""
2.绘制坐标点
"""
x = np.array([6])
y = np.array([6])
# scatter:绘制点，第1，2参数为坐标，s表示面积，c表示颜色，marker表示形状
plt.scatter(x, y, s=100, c='b', marker="*")
plt.show()
"""
3.绘制散点图，呈现正态分布
"""
# np.random:产生随机数
# normal(0, 3, 500):在0-3之间产生500个正态分布的随机数
x = np.random.normal(0, 3, 1000)
y = np.random.normal(0, 3, 1000)
# 将这1000个点中前500个画成红色圆形，后500个画成蓝色星型
plt.scatter(x[0: 500], y[0: 500], c='r', marker="o")
plt.scatter(x[500: 1000], y[500: 1000], c='b', marker="*")
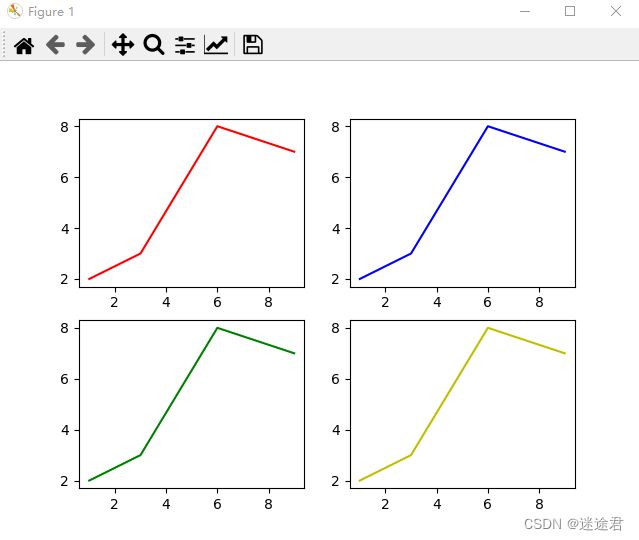
plt.show()
4.多界面绘制
import numpy as np
import matplotlib.pyplot as plt
"""
4.多界面绘制，其实就是在一figure窗口使用多个子图
"""
x = np.array([1, 3, 6, 9])
y = np.array([2, 3, 8, 7])
# 指定绘制的子图的位置
# 221表示二行2列, 共四个子图的第1幅图
# 222表示二行2列，共四个子图的的第2幅图
# 223表示二行2列，共四个子图的的第3幅图
# 224表示二行2列，共四个子图的的第4幅图
plt.subplot(221)
plt.plot(x, y, c='r')
plt.subplot(222)
plt.plot(x, y, c='b')
plt.subplot(223)
plt.plot(x, y, c='g')
plt.subplot(224)
plt.plot(x, y, c='y')
plt.show()
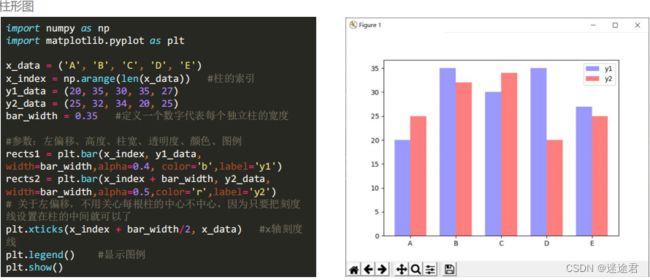
5.柱形图绘制
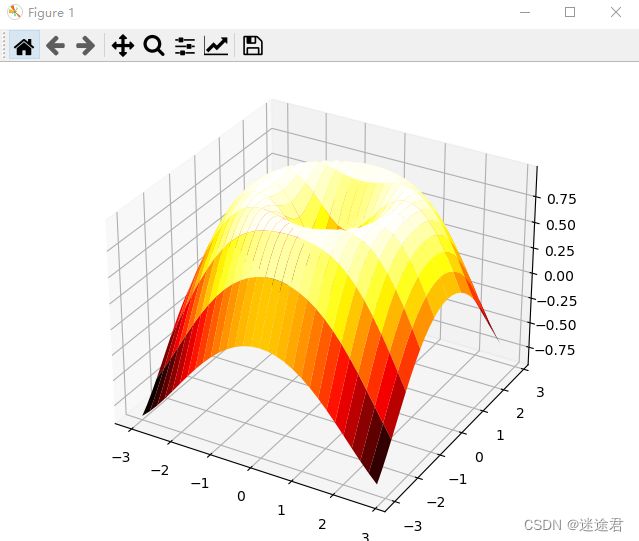
6.3D图形绘制
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
"""
绘制3d图
"""
# 创建窗口
fig = plt.figure()
# 在该窗口中创建3d绘图对象
ax = Axes3D(fig)
# 创建点的x和y坐标数组
x = np.arange(-3, 3, 0.2)
y = np.arange(-3, 3, 0.2)
# 网格化处理
x, y = np.meshgrid(x, y)
# 计算某个点到 原点的距离为半径
r = np.sqrt(x**2 + y**2)
# 以半径为基准，求它的正弦值为点的z轴坐标
z = np.sin(r)
# 绘制图像
ax.plot_surface(x, y, z, rstride=3, cstride=1, cmap="hot")
plt.show()
