机器学习笔记之玻尔兹曼机(一)基本介绍

引言

在受限玻尔兹曼机——模型表示(Representation)一节中以玻尔兹曼机为引，介绍了受限玻尔兹曼机。从本节开始，将正式介绍玻尔兹曼机。相比于它的表示和推断过程，我们更关注它在求解过程中出现的问题。

回顾：玻尔兹曼机的模型表示

玻尔兹曼机本质上是一个马尔可夫随机场(MArkov Random Field)，该概率图中结点均表示离散型随机变量，并被限定为伯努利分布。

并且，概率图中结点之间的边是随意的，并没有具体约束。但如果想要描述更加复杂的函数，自然需要结点之间复杂的边作为支撑：

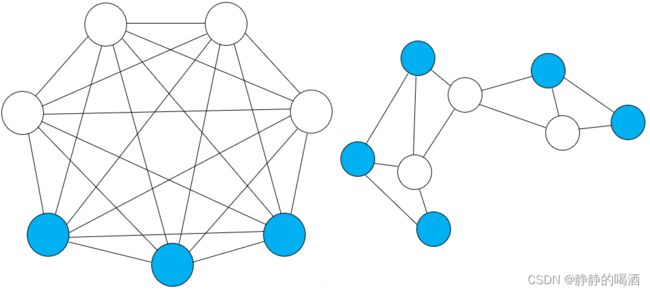
其中左图表示全连接玻尔兹曼机，无论是观测变量，还是隐变量，结点之间均存在边相连接；而右图同样表示玻尔兹曼机，只不过结点之间无明确约束，结点之间的边连接更加随意。

并且玻尔兹曼机并没有被严格要求一定有隐变量。也就是说，玻尔兹曼机可能是一个非隐变量模型，它的结点均由观测变量构成(Fully Observed Model)；与之相对的，从生成模型的角度考虑，我们更关注观测变量与隐变量相混合的概率图结构。

依然以包含隐变量的玻尔兹曼机为例，假设某玻尔兹曼机中包含观测变量集合$v$和隐变量集合$h$，并且$v$中的$\mathcal{D}$个分量和$h$中的$\mathcal{P}$个分量均服从伯努利分布：
$$\{\begin{array}{l}v=(v_1,v_2,\cdots ,v_{\mathcal{D}}{)}^T\in \{0,1{\}}^{\mathcal{D}}\\ h=(h_1,h_2,\cdots ,h_{\mathcal{P}}{)}^T\in \{0,1{\}}^{\mathcal{P}}\end{array}$$
关于结点之间边的权重，可以将其分成三类：

• 观测变量结点之间的边的权重表示：
  $$\mathcal{L}={\left[{\mathcal{L}}_{ij}\right]}_{\mathcal{D}\times \mathcal{D}}$$
• 隐变量结点之间的边的权重表示：
  $$\mathcal{J}={\left[{\mathcal{J}}_{ij}\right]}_{\mathcal{P}\times \mathcal{P}}$$
• 观测变量到隐变量结点之间的边的权重表示：
  同理，隐变量到观测变量结点之间的权重表示为$[{\mathcal{W}}_{ji}{]}_{\mathcal{P}\times \mathcal{D}}$,两者之间仅差一个转置，信息并没有发生变化。
  $$\mathcal{W}={\left[{\mathcal{W}}_{ij}\right]}_{\mathcal{D}\times \mathcal{P}}$$

至此，结点与边权重均已确定，关于玻尔兹曼机中随机变量(结点)的概率密度函数表示为：
$$\begin{array}{r}\mathcal{P}(v,h)=\frac{1}{\mathcal{Z}}\exp \{-\mathbb{E}(v,h)\}\end{array}$$
而能量函数$\mathbb{E}(v,h)$可根据玻尔兹曼机的结构表示，有：

• 从能量的角度考虑，$v_i\cdot {\mathcal{W}}_{ij}\cdot h_j$表示结点$v_i$和结点$h_j$之间的能量表示。
• 从概率角度考虑，无论是$v_i\cdot {\mathcal{W}}_{ij}\cdot h_j$还是$v_i\cdot {\mathcal{L}}_{ij}\cdot v_j$,还是$h_i\cdot {\mathcal{J}}_{ij}\cdot h_j$,它们的‘配分函数结果’均表示‘基于某结点的条件下，其他结点发生的概率结果’。
• 观测变量$v$和隐变量$h$均需要乘以$\frac{1}{2}$是因为无向图模型，仅需要计算一次边对应的能量即可，但实际上每条边在执行运算过程中，均加重了一次。
这里取上述‘全连接玻尔兹曼机’中的观测变量内部连接为例。

观察上图，观测变量内部仅包含三条边，仅需要计算$v_1\cdot {\mathcal{L}}_{12}\cdot v_2$和$v_3\cdot {\mathcal{L}}_{32}\cdot v_2$和$v_1\cdot {\mathcal{L}}_{13}\cdot v_3$这三项即可。但实际上却加了9次：
  ∑ i = 1 3 ∑ j = 1 3 v i ⋅ L i j ⋅ v j = ( v 1 , v 2 , v 3 ) ( L 11 = 0 , L 12 , L 13 L 21 , L 22 = 0 , L 23 L 31 , L 32 , L 33 = 0 ) ( v 1 v 2 v 3 ) \sum_{i=1}^3\sum_{j=1}^3 v_i \cdot \mathcal L_{ij} \cdot v_j = (v_1,v_2,v_3)\begin{pmatrix} \mathcal L_{11} = 0,\mathcal L_{12},\mathcal L_{13} \\ \mathcal L_{21},\mathcal L_{22} = 0,\mathcal L_{23} \\ \mathcal L_{31},\mathcal L_{32},\mathcal L_{33} = 0 \end{pmatrix}\begin{pmatrix} v_1 \\ v_2 \\ v_3 \end{pmatrix} i=1∑3​j=1∑3​vi​⋅Lij​⋅vj​=(v1​,v2​,v3​) ​L11​=0,L12​,L13​L21​,L22​=0,L23​L31​,L32​,L33​=0​ ​ ​v1​v2​v3​​ ​
  其中$\mathcal{L}$本身是实对称矩阵，对角线上包含$3$个零项；并且${\mathcal{L}}_{ij}={\mathcal{L}}_{ji}(i,j\in \{1,2,3\};i\ne j)$,因而剩余$6$项加重了三项，使用$\frac{1}{2}$将多加的项去掉。
  $$\begin{array}{rl}\mathbb{E}(v,h)& =-\left[\sum _{i=1}^{\mathcal{D}}\sum _{j=1}^{\mathcal{P}}{v}_i\cdot {\mathcal{W}}_{ij}\cdot h_j+\frac{1}{2}\sum _{i=1}^{\mathcal{D}}\sum _{j=1}^{\mathcal{D}}{v}_i\cdot {\mathcal{L}}_{ij}\cdot v_j+\frac{1}{2}\sum _{i=1}^{\mathcal{P}}\sum _{j=1}^{\mathcal{P}}{h}_i\cdot {\mathcal{J}}_{ij}\cdot h_j\right]\\ & =-\left[v^T\mathcal{W}\cdot h+\frac{1}{2}{v}^T\mathcal{L}\cdot v+\frac{1}{2}{h}^T\mathcal{J}\cdot h\right]\end{array}$$

至此，对应需要学习的模型参数表示为：
$$\theta =\{\mathcal{W},\mathcal{L},\mathcal{J}\}$$

模型参数的对数似然梯度

此时已经确定了玻尔兹曼机的概率密度函数，在模型参数的学习过程中，常用方法是极大似然估计。而对于玻尔兹曼机内部变量之间的复杂关系，可能没有办法去求解模型参数的精确解。因而，使用对目标函数求解梯度，通过梯度上升法对模型参数进行近似求解。

在实际求解过程中，仅知道观测变量的相关信息：通过具体样本。因而关于观测变量的边缘概率分布表示如下：
$$\mathcal{P}(v)=\sum _h\mathcal{P}(v,h)$$
这里定义$\mathcal{V}$是样本集合，样本集合$\mathcal{V}$中包含$N$个独立同分布的样本：
$$\mathcal{V}=\{v^{(1)},v^{(2)},\cdots ,v^{|\mathcal{V}|}\}|\mathcal{V}|=N$$
因此，关于$\mathcal{P}(v)$的对数似然结果表示如下：
$\frac{1}{N}$仅作为一个常数，对似然结果无影响。
$$\begin{array}{rl}\mathcal{P}(\mathcal{V};\theta )& =\frac{1}{N}\log \prod _{i=1}^N\mathcal{P}(v^{(i)};\theta )\\ & =\frac{1}{N}\sum _{i=1}^N\log \mathcal{P}(v^{(i)};\theta )\end{array}$$
对模型参数$\theta$求解梯度：
根据牛顿-莱布尼兹公式，将梯度符号与积分号(连加号)调换位置，并将常数$\frac{1}{N}$提到前面。
$$\begin{array}{rl}\frac{\partial \mathcal{P}(\mathcal{V};\theta )}{\partial \theta }& =\frac{\partial }{\partial \theta }\left[\frac{1}{N}\sum _{i=1}^N\log \mathcal{P}(v^{(i)};\theta )\right]\\ & =\frac{1}{N}\sum _{i=1}^N\frac{\partial }{\partial \theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]\end{array}$$

通过观察发现，仅需要对各具体样本的对数似然结果的梯度进行求解，最后相加即可。
在受限玻尔兹曼机——基于含隐变量能量模型的对数似然梯度中介绍了关于含隐变量能量模型的对数似然梯度通式：
$$\frac{\partial }{\partial \theta }\left[\log \mathcal{P}(v^{(i)};\theta )\right]=\sum _{h^{(i)},v^{(i)}}\left\{\mathcal{P}(h^{(i)},v^{(i)})\cdot \frac{\partial }{\partial \theta }\left[\mathbb{E}(h^{(i)},v^{(i)})\right]\right\}-\sum _{h^{(i)}}\left\{\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \frac{\partial }{\partial \theta }\left[\mathbb{E}(h^{(i)},v^{(i)})\right]\right\}$$

关于模型参数$\mathcal{W}$的对数似然梯度

以求解$\mathcal{W}$为例，求解$\mathcal{W}$的梯度：
这里依然需要一些‘矩阵论’中的矩阵求导 ->${\nabla }_{\mathcal{W}}\left[\mathbb{E}(v,h)\right]={\nabla }_{\mathcal{W}}\left[-v^T\mathcal{W}\cdot h\right]=-v{h}^T$
$$\begin{array}{rl}{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]& =\frac{\partial }{\partial \mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]\\ & =\sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[-v^{(i)}(h^{(i)}{)}^T\right]-\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \left[-v^{(i)}(h^{(i)}{)}^T\right]\\ & =\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]-\sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]\end{array}$$
因而关于模型参数$\mathcal{W}$的对数似然梯度可表示为：
$$\begin{array}{rl}\frac{1}{N}\sum _{i=1}^N\frac{\partial }{\partial \mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]& =\frac{1}{N}\sum _{i=1}^N{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]\\ & =\frac{1}{N}\sum _{i=1}^N\left\{\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]-\sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]\right\}\\ & =\frac{1}{N}\sum _{i=1}^N\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]-\frac{1}{N}\sum _{i=1}^N\sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]\end{array}$$
观察第二项，${\sum }_{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]$中$h^{(i)},v^{(i)}$被积分掉了，因而该式和$i$无关。因此有：
将第二项表示为期望形式，并且该期望基于的分布是$\mathcal{P}(h^{(i)},v^{(i)})$,即模型自身所有结点的联合概率分布。
$$\begin{array}{rl}\frac{1}{N}\sum _{i=1}^N\sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]& =\frac{1}{N}\cdot N\cdot \sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]\\ & =\sum _{h^{(i)},v^{(i)}}\mathcal{P}(h^{(i)},v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]\\ & ={\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(h^{(i)}{)}^T\right]{\mathcal{P}}_{model}\Rightarrow {\mathcal{P}}_{model}(h^{(i)},v^{(i)})\end{array}$$
对应的，第一项可表示为：
根据蒙特卡洛方法的逆推过程，可以将其理解成‘期望的期望’，而${\sum }_{i=1}^N$可以看作是从‘真实分布’${\mathcal{P}}_{data}$中抽取出的$N$个样本。
$$\begin{array}{rl}& \frac{1}{N}\sum _{i=1}^N\sum _{h^{(i)}}\mathcal{P}(h^{(i)}\mid v^{(i)})\cdot \left[v^{(i)}(h^{(i)}{)}^T\right]\\ & =\frac{1}{N}\sum _{i=1}^N\left\{{\mathbb{E}}_{\mathcal{P}(h^{(i)}\mid v^{(i)})}\left[v^{(i)}(h^{(i)}{)}^T\right]\right\}\\ & \approx {\mathbb{E}}_{{\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})}\left\{{\mathbb{E}}_{\mathcal{P}(h^{(i)}\mid v^{(i)})}\left[v^{(i)}(h^{(i)}{)}^T\right]\right\}\end{array}$$
最终使用一个符号${\mathcal{P}}_{data}$进行表示。其中$\mathcal{P}(h^{(i)}\mid v^{(i)})$表示某样本$v^{(i)}$对应模型中隐变量的后验概率，因而它是基于模型产生的概率分布。因为在样本分布中，$h^{(i)}$无法被观测，是不存在的。
$$\begin{array}{rl}& {\mathbb{E}}_{{\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})}\left\{{\mathbb{E}}_{\mathcal{P}(h^{(i)}\mid v^{(i)})}\left[v^{(i)}(h^{(i)}{)}^T\right]\right\}={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]\\ & {\mathcal{P}}_{data}\Rightarrow {\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})\cdot {\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})\end{array}$$

终上，模型参数$\mathcal{W}$的对数似然梯度可表示为：
$$\begin{gathered} \frac{1}{N}\sum _{i=1}^N{\nabla }_{\mathcal{W}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(h^{(i)}{)}^T\right] \\ \{\begin{array}{l}{\mathcal{P}}_{data}={\mathcal{P}}_{data}(v^{(i)}\in \mathcal{V})\cdot {\mathcal{P}}_{model}(h^{(i)}\mid v^{(i)})\\ {\mathcal{P}}_{model}={\mathcal{P}}_{model}(h^{(i)},v^{(i)})\end{array} \end{gathered}$$

关于模型参数$\mathcal{L},\mathcal{J}$的对数似然梯度

关于模型参数$\mathcal{L},\mathcal{J}$和$\mathcal{W}$的求解过程完全相同，只不过针对不同的参数项进行求导而已，这里就不再描述过程了。对应梯度表示如下：
关于$\mathcal{L}$的项${\nabla }_{\mathcal{L}}[\mathbb{E}(v,h)]={\nabla }_{\mathcal{L}}\left[v^T\mathcal{L}\cdot v\right]=v{v}^T$
关于$\mathcal{J}$的项${\nabla }_{\mathcal{J}}[\mathbb{E}(v,h)]={\nabla }_{\mathcal{J}}\left[h^T\mathcal{J}\cdot h\right]=h{h}^T$
$$\begin{array}{rl}\frac{1}{N}\sum _{i=1}^N{\nabla }_{\mathcal{L}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]& ={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[v^{(i)}(v^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[v^{(i)}(v^{(i)}{)}^T\right]\\ \frac{1}{N}\sum _{i=1}^N{\nabla }_{\mathcal{J}}\left[\log \mathcal{P}(v^{(i)};\theta )\right]& ={\mathbb{E}}_{{\mathcal{P}}_{data}}\left[h^{(i)}(h^{(i)}{)}^T\right]-{\mathbb{E}}_{{\mathcal{P}}_{model}}\left[h^{(i)}(h^{(i)}{)}^T\right]\end{array}$$

下一节将介绍基于马尔科夫链蒙特卡洛方法(MCMC)求解各参数的梯度，从而实现随机梯度上升过程。

相关参考：
(系列二十八)玻尔兹曼机1-介绍
(系列二十八)玻尔兹曼机2-log似然的梯度