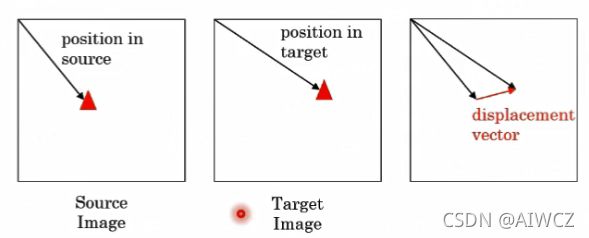
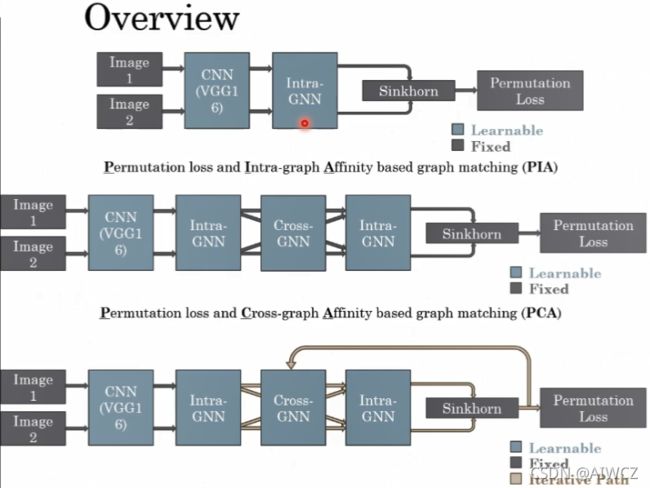
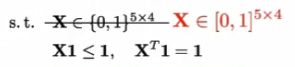Graph Matching
受严骏驰老师讲座内容启发，最近项目中一个关键问题才找到了一些解决途径，为了能够快速对Graph Matching的起源和发展现状有一定了解，从而形成知识体系来更好得解决问题，准备慢下来，把这些知识沉淀下来，写成一篇blog。
(讲座链接：https://www.bilibili.com/video/BV1Zf4y1S7Zr)
Graph Matching 属于一种组合优化问题，图这类数据结构形式在推荐系统、知识图谱等中最为常见，而在计算机视觉领域中，为解决少样本学习或目标检测类别长尾分布等，图结构也有较多工作采用。
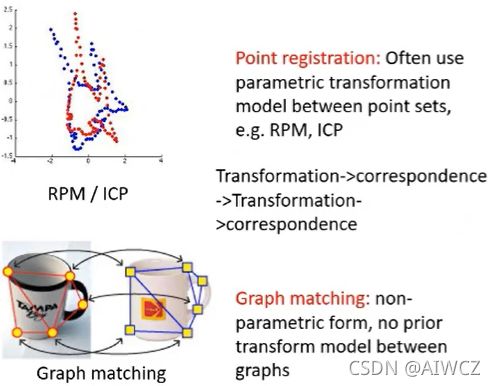
1. Graph matching 和 Registration 的区别？
用一句话说：Registration需要在变换空间中寻找一种最有效的变换，这种变换能够使两幅图像之间在某种意义上达到匹配，而Graph matching是一种非参数的模型，只关心point之间和edge之间的对应关系。
2. 最原始的Graph matching有哪些步骤？
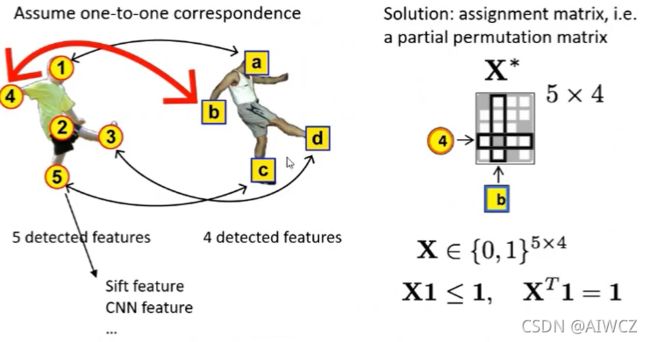
①提取特征(特征检测)：1. SIFT , 2. CNN
②初始化assignment matrix
a. 1st-order Feature
Node correspondence, 此时是 Feature Matching问题，是linear的。
b. 2nd-order Feature
此时才是 Graph Matching 问题，是quadratic(二次)的，因此其也被称作**QAP(Quadratic Assignment problem)**问题。
③建立Kp(Kq)存储相似度信息
a. Kp矩阵。
下图中的Cst即是一种相似度计算方式，两两进行计算来填充。
b. Kq矩阵
c. Affinity Matrix
进一步得，为了让存储相似度信息更加方便，采用Affinity Matrix代替Kp、Kq存储的相似度信息。
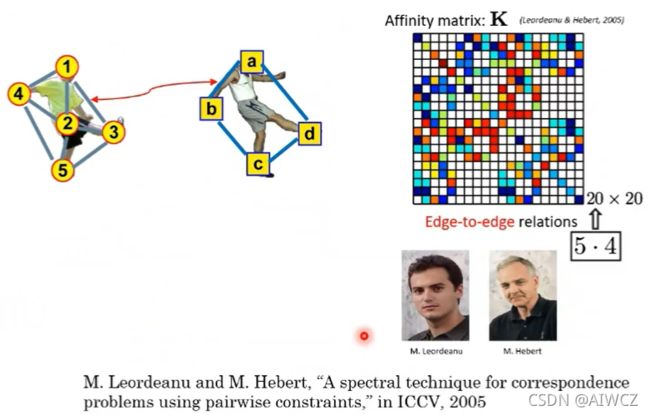
d. 上图Affinity Matrix的解释：
横纵轴每格代表的节点对相同，事先进行编码。
例如，以左上角为原点，向右向下分别代表着，1a,1b,1c…。
1.对角线(Diagonal)元素20个，代表原Kp矩阵信息，例如1b - 1b，表示1节点和b节点的相似度。
2.非对角线元素则代表原Kq矩阵信息，例如3b - 5c，则代表35这条边和bc边的相似性。
即每个点构成一个超点，形成下图中的 Association Graph。
④求解目标：找到一个assignment matrix，使得总和相似性最大化
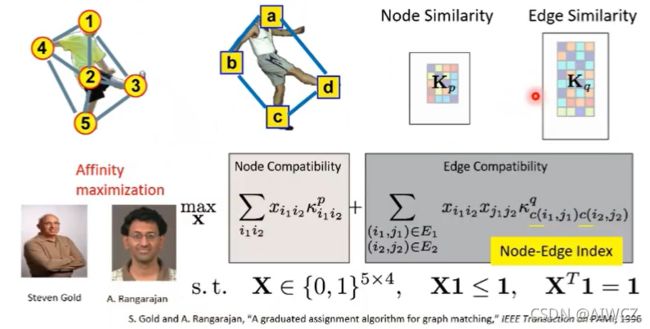
or:
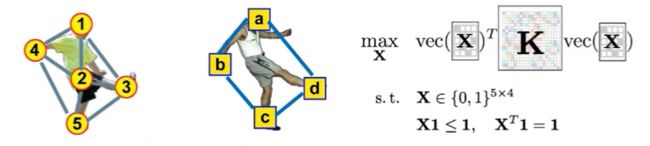
注意：这里的vec(X*)是对X*按 列 向量化，变成20X1的矩阵，转置后变成1X20。因此最后三个矩阵相乘是一个标量，对这个标量最大化即可。
3. 有哪些常用的改进手段？
①松弛
当上图中的K矩阵没有特殊性质时，解X*是一个NP-hard问题，因而对于Graph Matching问题，松弛手段的使用是常见的。
a. Spectral Approximation
去掉原始的 离散域限制条件：
化为模的形式，使得X*向量化后的二范数 为1。
即：
缺点：松弛后将不太紧凑
优点：求解速度快，利用类似谱方法求解，求特征值、特征向量等等。
相关文章：
b. Double-stochastic Approximation
一种较为紧凑的松弛策略，仍保留原始不等式约束，将X*原本属于的0、1二值矩阵，松弛到[0,1]这一实数域。
即：
缺点：速度相较于a.来说慢一些
优点：紧凑
相关文章：
②考虑更高阶信息
我们在上面的讲解中有提到1st-order Feature和2nd-order Feature，从1st到2nd包含了更多的信息，一个自然而然的想法，是否可以扩展到 3-Order 及以上，形成一个超图，来对更多的信息进行建模泛化。
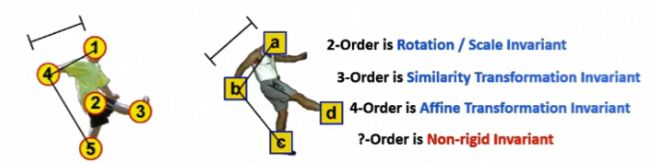
但在节点数较多时，相关的组合数会指数爆炸，因而现有的方法还是以二阶为主，但通过图嵌入的方式，有可能将高阶信息向低阶嵌入。
③K矩阵分解
从上面的描述可以看到，K矩阵是十分稀疏的，其空间规模远大于节点的Kp矩阵和边的Kq矩阵之和，因而找到一种将K矩阵进行分解的方法，用时间来换空间，就很有必要。
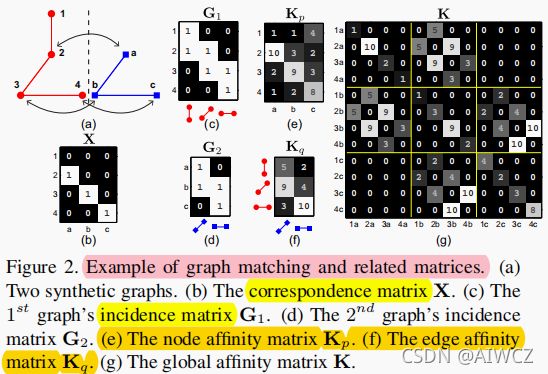最后推导出K矩阵可由上述几个小矩阵(G1、G2、Kp、Kq)做克罗内克(Kronecker)积。
即：
相关文章：
补充知识：
哈达玛积(Hadamard products)，完全的对应元素相乘，也叫 基本积。
克罗内克积(Kronecker products)，张量积的特殊形式，见百度。
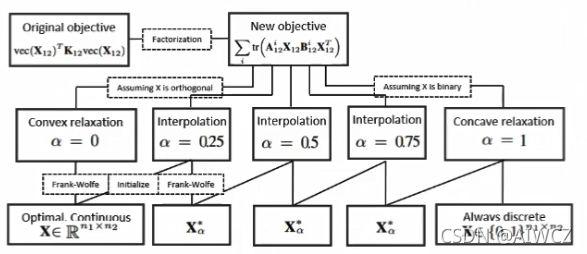
④Path-following optimization
基于分解模型可以提出一个路径跟踪算法，一开始做一个图优化的松弛，把原目标函数变成一个凸函数。图优化的好处在于 对初始解不敏感，最开始能够快速逼近最优解，而后再增大约束，变成凹函数，最终能够到达 自然收敛到离散解的目的，避免了连续域解激活时的偏差。
⑤小结
传统非机器学习(深度学习)方法，主要有两条路径：
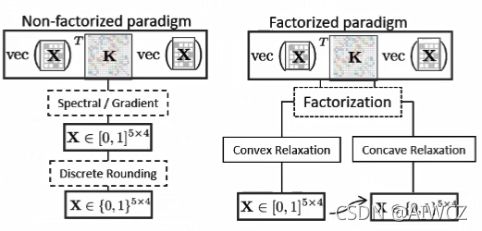左列：不分解
右列：分解了，空间换时间
4. 从图的两两匹配到多图匹配？
在实际场景中，往往有多个图像需要同时匹配，此时两两图匹配的方式不仅速度较慢，而且还无法利用多个图的整体信息，影响鲁棒性。
相关工作：
相关文章解读，挖个坑，后面写
5. 目标函数建模的优化
多图匹配引入了一些正则，本质上是优化目标函数的建模。在多数Graph Matching问题中目标函数的全局最优解，并不是物理意义的最优解，因而一个自然而然的想法是，能否通过一些学习手段来优化目标函数。
我们回到最初的Graph Matching中，我们是假定了，点与点之间，边与边之间的匹配重要程度是完全相同的，但在现实问题中并不是这样，我们需要对某些点和某些边更注意，这和纯CV里的 注意力机制有些相似。
a. “Learning Graph Matching” TPAMI2009 and " Learning Graphs to Match" ICCV2013
6. 基于深度学习的图匹配
a.“Deep Learning of Graph Matching.” CVPR2018 最佳论文提名
论文中非常详细的反向传播推导，暂时挖个坑，后面再解读。
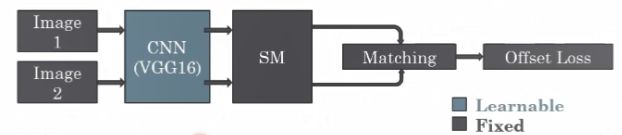
前向推理的思路是很简单的：
①给定两个图像
②用CNN去提取关键点的特征（即此时可以形成图结构并计算相似性）
③用谱方法SM计算特征值、特征向量（前文有讲解）
④做Matching算平移误差
⑤梯度回传更新CNN权重
本文局限
①SM是一个近似解，并不是针对Graph Matching的最优方案。
②SM复杂度高。
③offset Loss的损失函数有缺陷，类似光流损失函数，对 距离位移敏感。而对于匹配问题，不应该在意形变、物理平面差距，而应该最在意配没有配准。
即：
针对上述局限的改进:
b. Learning Combinatorial Embedding Networks for Deep Graph Matching(ICCV19)
待续