深度森林论文阅读笔记

本文是《机器学习》作者周志华教授和冯霁博士在2017年2月28日发表的论文《Deep Forest: Towards An Alternative to Deep Neural Networks》的阅读笔记，因此本文不会一字一句的翻译过来，但会加入我自己的理解，如有谬误请读者指正。新智元（ http://chuansong.me/n/1621631051734）对此文也有一篇翻译。

周志华教授和冯霁博士提出了“深度森林”，这是一种可以与深度神经网络相媲美的基于树的模型。这篇论文出来几天就已经引起巨大反响，可能一方面是由于深度学习实在太火，周老师敢于挑战深度学习的“权威”，另一方面可能是周老师的《机器学习》实在太多粉丝了。

现时，深度神经网络（下统一简称为DNN，这里DNN泛指所有深度网络，不单是深层的BP网络）运用很广泛，这基本上来源于深度学习在不同应用场景中都有不可思议的甚至令人耳目一新的结果，尤其是在计算机视觉和语音识别之类的领域。

尽管DNN有很令人惊叹的应用，但同时它也有不足之处，主要表现为：

1.DNN需要使用大量的数据进行训练。哪怕是现在的大数据时代，我们都缺乏足够的训练数据——因为标注类别是个成本很高的事情。

2.DNN因其复杂难懂的结构和庞大的计算能力需求，一定程度上使得很多尝试被迫“知难而退”——因为商业应用上不单只追求正确，更重要的是计算效率，科技公司是坚决不干成本高的事情。

3.DNN有很多超参数，而且这些超参数对模型结果有着至关重要的影响，所以对超参数的选取也是个很重要的事情——超参数就好比如一首歌曲中的节拍、强弱、速度等因素，即便音符一模一样，但这些因素的不一样就会产生不同的效果。

DNN很重要的一个点是有很强大的“表征学习”（representation learning）能力，个人认为“表征学习”意思是将输入数据在空间上映射到另一个情况，例如BP网络可以将输入数据扭曲、旋转等，CNN可以用采样窗口对输入图像抽象化，抽取重要的轮廓或者特征。不管怎么样，输入数据经过一层的转换之后输出的都是一个representation data，而这输出的数据又往下生成更抽象的特征。DNN需要用大量的数据进行训练，那模型本身也应该需要是个庞大的结构，这点也部分的解释了为什么DNN如此的复杂难懂，至少它比SVM等传统机器学习算法复杂多了。我们可以做个大胆的假设，如果我们把一些好的属性应用在其他适合的算法上，那么我们也很可能会得到与DNN差不多的效果，甚至可能只有更少的缺点。

这里提出一个新的模型gcForest（muti-Grained Cascade Forest，多粒度串联森林），它是基于树的集成方法，通过对树组成的森林来集成并前后串联起来达到表征学习的效果。它的表征学习能力可以通过对高维输入数据的多粒度扫描而进行加强。串联的层数也可以通过自适应的决定从而使得模型复杂度不需要成为一个自定义的超参数，而是一个根据数据情况而自动设定的参数。值得注意的是，gcForest会比DNN有更少的超参数，更好的一点在于gcForest对参数是有非常好的鲁棒性，哪怕用默认参数也可以获得很棒的结果。换句话来说，gcForest相对于DNN，不仅超参数更少，而且对超参数的依赖性也更低。因为这样，gcForest的训练更为便捷，理论分析也更为清晰，这并不是说树比神经网络更好去解释，就单纯从超参数来说，更少超参数意味着更少的主观设定（虽然设定超参数也是结果导向的，但通常为什么要这么设是没有一个很好的理由去解释）。周教授说，在他们的实验中，gcForest不仅仅效果可以媲美DNN，而且单机跑gcForest所需的时间与带GPU加速跑DNN是相仿的，因为gcForest是可以并行计算。

周教授提出gcForest是为了什么？固然gcForest并非为了替代DL而生，而是由于DL在很多情况下，对数据量、超参数调优、设备计算能力都有很高的要求，所以gcForest希望是能在某些场合替代高开销的DNN。

进入正题了，从gcForest的名字来看，至少要包含三个信息：

1.这个模型是串联结构的

2.模型是多粒度扫描的

3.是一种基于树集成的模型

森林级联结构

gcForest采用了深度网络的一层叠一层的结构，从前层输入数据，输出结果作为下层的输入。基本结构如图：

如上图所示，每一层都是由决策树组成的森林组成的，也就是每层都是“集成的集成”。但注意，这里每层都是由两种不同的森林所组成，这是因为周教授在2012年发表论文说，多样的结构对集成学习来说是很重要的。这一点我个人很赞同，毕竟是集成智慧，不同个体之间总需要有高有低的，需要有所参差这样的集成会更有意义，但当然，我没有证明过这种想法，周教授已经做过了。那这里所谓的两种森林是指什么呢？这里举了个简单的例子，例如说图中黑色的完全随机森林，而蓝色的是普通随机森林。完全随机森林是由1000棵决策树组成，每棵树 随机选取一个特征作为分裂树的分裂节点，然后一直生长直到每个叶节点细分到只有1个类别或者不多于10个样本。类似的，普通随机森林由1000棵决策树构成，每棵树 通过随机选取sqrt(k)（k表示输入特征维度，即特征数） 个候选特征，然后通过gini分数筛选分裂节点。所以两种森林的主要区别在于候选特征空间，完全随机森林是在完整的特征空间中随机选取特征来分裂，而普通随机森林是在一个随机特征子空间内通过gini系数来选取分裂节点。周教授这里只提到完全随机森林中决策树的生长规则——完全或近乎完全生长，但没有提到普通随机森林的生长规则，按经验应该是可以设定停止生长规则或者采用后剪枝来修剪模型的。每个森林里决策树的数量其实是个超参数，这点会在稍后再进行讨论。

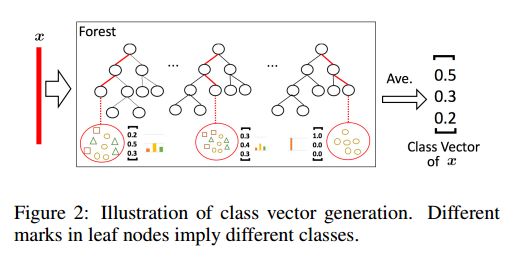
因为决策树其实是在特征空间中不断划分子空间，并且给每个子空间打上标签（分类问题就是一个类别，回归问题就是一个目标值），所以 给予一条测试样本，每棵树会根据样本所在的子空间中训练样本的类别占比生成一个类别的概率分布，然后对森林内所有树的各类比例取平均，输出整个森林对各类的比例。例如下图所示，这是根据图1的三分类问题的一个简化森林，每个样本在每棵树中都会找到一条路径去找到自己对应的叶节点，而同样在这个叶节点中的训练数据很可能是有不同类别的，我们可以对不同类别进行统计获取各类的比例，然后通过对所有树的比例进行求均值生成整个森林的概率分布。

由此，每个森林都会生成长度为C的概率向量，如果一层有N个森林，那么每个森林生成的C个元素会拼接在一起，组成C*N个元素向量，这就是一层的输出。 在这基础上，还要把源输入特征向量拼接上去（如图1每层的粗红线部分），这样就组成了下一层的输入。这里要注意，稍后会提到特征向量的多粒度扫描，暂时请忽略粗红线这里的部分。

为了避免过拟合现象，这里每个森林的训练都采用了K-fold交叉验证，即每个样本都会被用作k-1次训练以及k-1次的检验，所以 每个森林生成的概率分布并不是来自同一批训练数据的训练结果，而是通过对交叉检验之后的k-1次结果求平均，再输出结果。一层结果输出之后，这事都还没完，我们会用此模型来对一个检验集进行估计，如果得到的结果看起来已经快要撞上天花板了（周教授没有讲解这部分，个人觉得就是准确率或者误差趋于饱和了），那训练就会被终止。这个操作很关键，因为它相当于 自动决定了层数，对模型复杂度的自适应调节使得gcForest可以可伸缩的应用在不同规模训练数据集上，同时也就避免了DNN固定的模型复杂度不能在少量数据集上很好应用的尴尬。

多粒度扫描

在图像识别中，位置相近的像素点之间有很强的空间关系，因为CNN的采样窗口可以很好的处理这个空间上的关系；RNN能很好的处理在时间序列上有关联的。受到深度学习模型的启发，gcForest也利用了多粒度扫描（mult-grained scanning）对级联森林进行增强。

多粒度扫描其实是引用了类似CNN的一个滑动窗口，例如说我们现在有一个400维的样本输入，现在设定采样窗口是100维的，那我们可以通过逐步的采样，最终获得301个子样本（因此这里默认的采样步长是1，所以得到的子样本个数 = (400-100)/1 + 1）。如果输入的是一个20*20的图片，利用一个10*10的采样窗口，就可以获得121个子样本（对每行和每列都是 (20-10)/1 + 1 = 11，11*11 = 121）。所以，整个多粒度扫描过程就是：先输入一个完整的P维样本，然后通过一个长度为k的采样窗口进行滑动采样，得到S = (P - K)/1+1 个k维特征子样本向量，接着每个子样本都用于完全随机森林和普通随机森林的训练并在每个森林都获得一个长度为C的概率向量，这样每个森林会产生长度为S*C的表征向量（就是经过随机森林转换并拼接的概率向量），最后把每层的F个森林的结果拼接在一起得到本层输出。

这里只是用一种大小的滑动窗口来举例子，但实际上是可以利用多种大小的滑动窗口进行采样，这样可以获得更多的特征子样本，真正达到“多粒度”扫描的效果，这种情况接下来就会介绍到。

gcForest的全过程与超参数

gcForest的全过程可以由下图表示：

上图表示，输入一个400维的特征向量，准备100、200、300维的三个不同大小的滑动采样窗口分别对输入特征进行采样，这样分别会得到301个100维子样本，201个200维样本和101个300维样本。若训练集中共有m条训练样本，对100维的采样窗口来讲，就可以获得301 * m 个100维训练样本。采样出来的所有子样本都会被用作完全随机森林和普通随机森林的训练，假设这是一个C分类问题，那么，100维的采样窗口会产生长度为301*C的向量，200维的产生201*C的向量，300维的产生101*C的向量，把它们拼接起来，整层输出就是一个长度为2*(301+201+101)*C的向量了（注：这里的2表示2种森林，603*C是每种森林的生成长度）。

让我们暂停一下，回想一下，在森林级联时提到每层森林的集成输出都会拼接上一个“源特征向量”。由于源特征向量已经被滑动抽样再经过森林生成了“再表征”（re-representation）向量，所以我们需要拼接的就不再是“源特征向量”，而是经过多粒度扫描的“再表征向量”。

如图，源特征向量400维经过多粒度扫描之后变成了3618维的再表征向量，这3618维向量会往下传递到级联森林。假如级联森林每层固定是由4个森林组成而且这是一个三分类问题，那么每层生成的输出是长度为12的表征向量，这个表征向量跟3618维再表征向量拼接再一起，变成了3630维的向量并作为下一层级联森林的输入， 像这样层层往下传递，直至检验集建议停止层级加深。到最后的输出层，我们对所有森林生成的各类概率进行求平均。

对比一下DNN和gcForest的主要参数：

可以看到gcForest的主要参数是：

1.多粒度扫描的森林数

2.每个森林的决策树数

3.树停止生长规则

4.滑动窗口数量和大小

5.级联的每层森林数

6.每个森林的决策树数

7.树停止生长规则

接下来就是一系列的实证了，周教授分别从手写识别、人脸识别、音乐片段识别等等方面的数据集进行验证，证明gcForest是一个可以媲美DNN而且比传统机器学习模型有明显优势的模型，此处就不加详述。另外，多粒度扫描是gcForest的一个重要组件，它在处理序列上或空间上有关联的数据时能明显提高模型效果。

总的来说，gcForest有如下若干有点：

1.计算开销小

2.模型效果好

3.超参数少，模型对超参数调节不敏感，并且一套超参数可使用到不同数据集

4.可以适应于不同大小的数据集，模型复杂度可自适应伸缩

5.每个级联的生成使用了交叉验证，避免过拟合

6.相对于DNN这个大黑盒，gcForest更容易进行理论分析