深度强化学习-DQN 算法及 Actor-Critic 算法-笔记（五）

DQN

Q-learning

状态价值函数 State Value Function

状态价值函数的贝尔曼方程

记策略 π 的状态值函数为 V^π(s_t) ，它表示在状态 s_t 下带来的累积奖励 G_t 的期望，具体公式为：

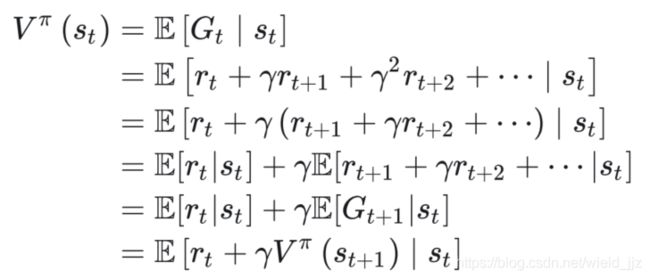
如何衡量状态价值函数？

有两种做法：

1. 基于蒙特卡洛的方法Monte-Carlo(MC)：critic 观察 π 进行游戏的整个过程, 直到该游戏回合结束再计算累积收益（通过比较期望收益和实际收益G，来训练critic）。有时一个游戏回合可能会很长，这个等到游戏回合结束再计算收益的方法训练起来会很慢，因此引入另外一种方法 Temporal-difference（TD）
2. 时序差分的方法Temporal-difference (TD)：时序分差算法计算的是两个状态之间的收益差（通过比较期望差异与实际差异r之间的差别来训练critic）。
   

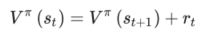
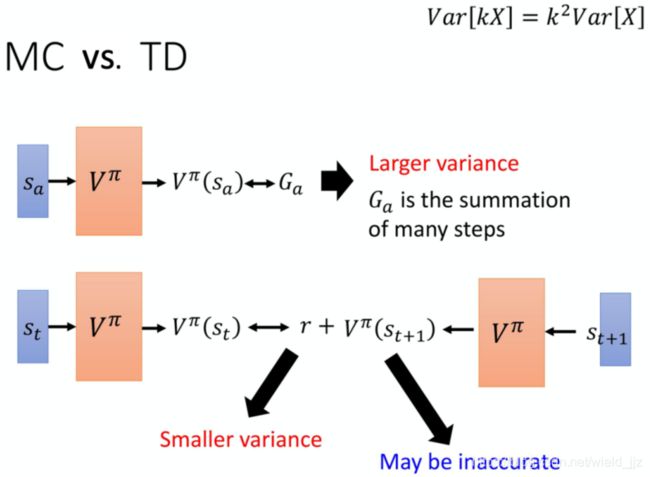
MC vs. TD

• MC：方差大。因为MC的方法收集的是每个完整的回合，而对于某个状态的累计收益G也是集合了很多步。
• TD：方差小，但是可能不准确。在TD的方法中，用前一步的状态价值与下一步的状态价值之差r来更新，所以单步更新大大减小了方差，但是同样因为r的随机性（因为在同一个状态下采取同一个动作，计算出来的reward也不一定相同），但是这个随机性比MC方法中多步的r合计的随机性要小。

其实，目前来看，使用TD的方法是比较常见的，MC方法现在比较少用。
举个例子说明蒙特卡洛方法和时序差分方法的区别：

状态-动作价值函数 State-action Value Function

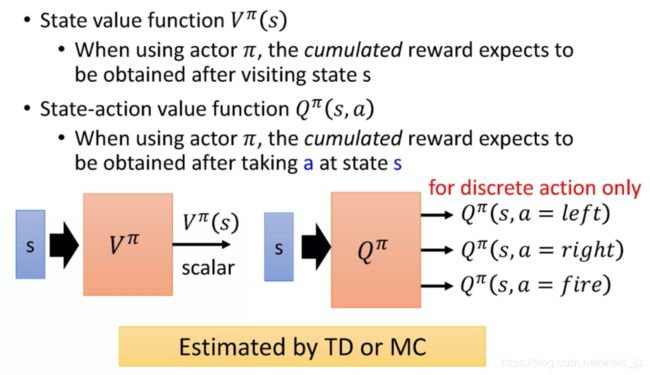
对于给定的actor π, 在状态s采取行动a预计能够得到的累计收益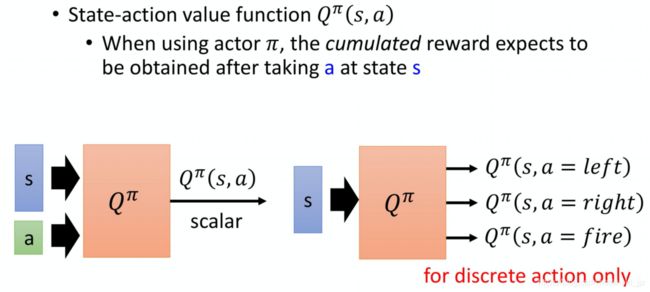

state value function 与 state-action value function

1. state value function 的 input 是一个 state，它是根据 state 去计算出，看到这个state 以后的 expected accumulated reward 是多少。
2. state-action value function 的 input 是一个 state 跟 action 的 pair，它的意思是说，在某一个 state 采取某一个action，假设我们都使用 actor π，得到的 accumulated reward 的期望值有多大。
   注意：actor π 在 state s 时采取的动作不一定是action a，但是Q-function是规定只有在state s 下才强制采取action a，接下来就进入自动模式， 让actor π 继续玩下去， 得到的expected reward 才是 Q^π(s,a)。

Q-function 有两种写法：

• input 是 state 跟action，output 就是一个 scalar； （连续动作）
• input 是一个 state s，output 就是好几个 value。（离散动作）

这里要知道两点：

• 什么叫做better？
  不管在哪个state，用π’跟环境做交互得到的expected reward一定大于π。
  证明：
  

• 怎么找这个π’？
  
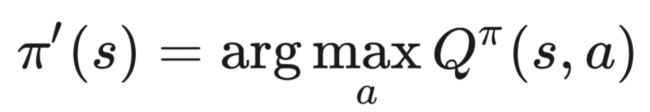
  π’是根据Q-function推出来的。上式的右边要求arg max ，如果这里的动作是离散的，可以一个个带进去看谁的Q大就行，但是如果动作是连续的，这里求解arg max就会有问题。

Q-learning：

• 使用一个初始的actor π 与环境进行互动
• 学习该actor对应的 Q function
• 一定存在另外一个表现更好的actor π ′ , 用这个更好的actor来替代原来的actor
• 重复上述步骤

目标网络 Target Network

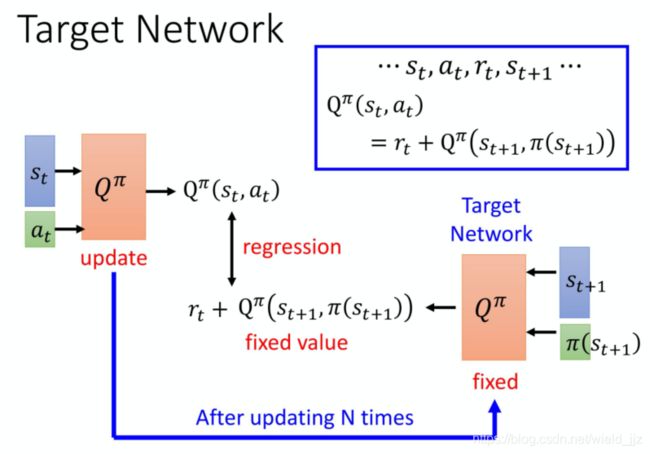
下式是我们熟悉的TD方法：

所以最简单的想法就是固定一个网络，这里固定的是上式右边的网络，在训练的过程中我们只更新左边的网络参数，而不更新右边的target网络的参数，这样就变成了一个回归问题。我们希望魔性的输出与目标值越接近越好，通常就会采取最小化二者的MSE（mean square error）

在实现的时候，你会把左边的 Q-network update 好几次以后，再去用 update 过的 Q-network 替换这个 target network 。但它们两个不要一起动，它们两个一起动的话，结果会很容易坏掉。一开始这两个 network 是一样的，然后在 train 的时候，你会把右边的 Q-network fix 住。你在做 gradient decent 的时候，只调左边这个 network 的参数，那你可能update 100 次以后才把这个参数复制到右边的 network 去，把它盖过去。把它盖过去以后，你这个 target value 就变了。就好像说你本来在做一个regression problem，那你 train 后把这个 regression problem 的 loss 压下去以后，接下来你把这边的参数把它 copy 过去以后，你的 target 就变掉了，接下来就要重新再
train。

探索 Exploration

• ε-greedy：在采取action的时候，actor会有 1 − ϵ 的概率选择使得Q值最大的a，随着训练时间变长，ϵ 的值逐渐减小，在后期actor选择最大Q值对应的a才会变大。
• Boltzmann：和 policy gradient 类似, 根据一个概率分布来进行采样。

经验重放 Experience Replay

Experience Replay 会构建一个 Replay Buffer（Replay Memory）。有一个policy π 去跟环境做互动，在这个过程中收集数据，把收集到的每一条数据放进Replay Buffer里，记录着在state s_t，采取某个action a_t，得到了reward r_t，然后跳到了state s_t+1。

注意： replay buffer 里面的 experience 可能是来自于不同的 policy。因为每次拿π去跟环境做互动的时候，，你可能只互动 10000 次，然后接下来你就更新你的π了。但是这个 buffer 里面可以放 5 万笔资料，所以 5 万笔资料可能是来自于不同的 policy。Buffer 只有在它装满的时候，才会把旧的资料丢掉。所以这个 buffer 里面它其实装了很多不同的 policy 的 experiences。

如何利用经验重放来训练Q函数？

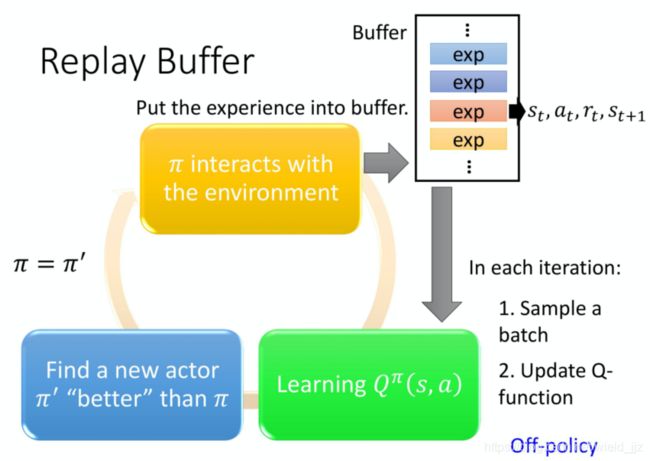
这是一个 off=policy 的做法。因为本来我们的 Q 是要观察 π 的 experience，但实际上存在你的 replay buffer 里面的这些 experiences 不是通通来自于 π ，有些是过去其他的 π 所遗留下来的 experience。因为你不会拿某一个 π 就把整个 buffer 装满，然后拿去测 Q-function，这个 π 只是 sample 一些data 塞到那个 buffer 里面去，然后接下来就让 Q 去 train。所以 Q 在 sample 的时候， 它会 sample 到过去的一些资料。

这么做的好处是什么？

• 减少跟环境做互动的次数，在训练时，一些过去的不同的 policy 所得到的 experience 可以放在 buffer 里面被使用很多次，这样会使得训练过程比较高效。
• buffer 中的experience 是来自于不同的policy，这样sample 到的一个 batch 里面的 data 会是比较 diverse（离散），同一个batch里的数据越离散越好。

DQN算法

DQN 和 Q-learning 有什么不同？

整体来说，DQN 与 Q-learning 的目标价值以及价值的更新方式都非常相似，主要的不同点在于：

1. DQN 将 Q-learning 与深度学习结合，用深度网络来近似动作价值函数，而 Q-learning 则是采用表格存储；
2. DQN 采用了经验回放的训练方法，从历史数据中随机采样，而 Q-learning 直接采用下一个状态的数据进行学习。

Tips of Q-learning

Double DQN

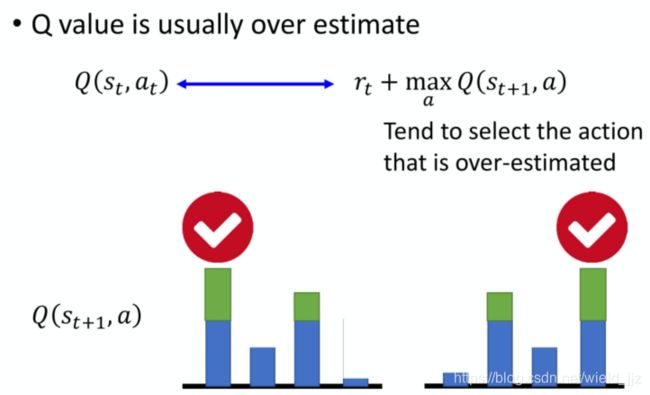
• 为什么要有DQN？
  由于Q值总是基于使得Q最大的action得出的，因此会趋向于被高估，于是引入double DQN

• 为什么 Q 值总是被高估了呢？
  

• 如何解决这里的target总是太大的问题？
  使用两个Q function（因此称为double）, 一个用来选择行动action，另外一个用来计算Q值，通常会选择target network来作为另外一个用于计算Q值的Q‘ function。
  如果Q高估了 a 从而被选择， Q’ 会给这个被选择的a一个合适的Q值；
  如果Q’会高估某个action a，这个action并不会被Q选择到。
  

• 哪来的Q跟Q’呢？哪来两个network呢？
  在实现上，你有两个 Q-network， 一个是 target 的 Q-network，一个是真正你会 update 的 Q-network。所以在 Double DQN 里面，你的实现方法会是拿你会 update 参数的那个 Q-network 去选 action，然后你拿 target 的network，即固定住不动的 那个network 去算 value。

Dueling DQN

只对网络结构进行改变！

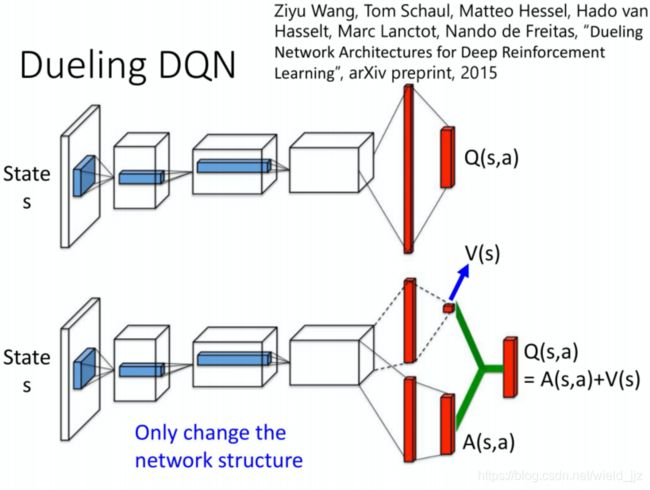
• Dueling DQN 是怎么改了 network 的架构呢？
  这里计算出来的值有两个:
  V(s): 对不同的state都有一个值，表示静态环境，状态s所具有的价值。
  A(s,a): 向量，对不同的state，不同的action都会有一个值。
  

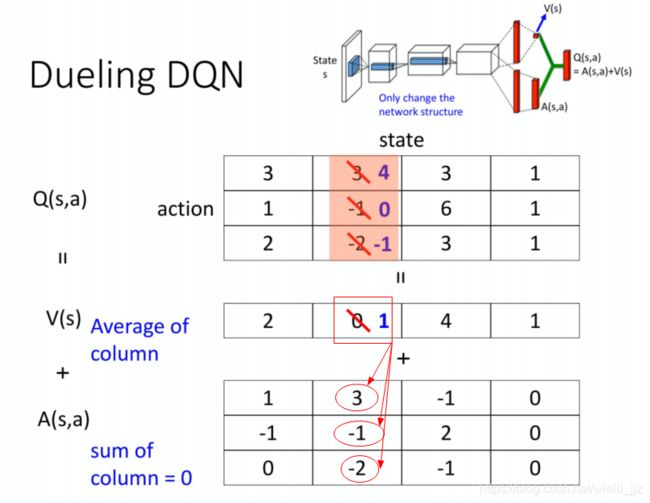
• 这样改的好处
  所以有可能说你在某一个 state，你明明只 sample 到这2 个 action，你没 sample 到第三个 action，但是你其实也可以更改第三个 action 的 Q value。这样的好处就是你不需要把所有的 state-action pair 都 sample 过，你可以用比较高效的方式去把 Q value 估计出来。

• 如何避免机器学到 V 永远都是 0，使得A 总是等于 Q这种情况？
  
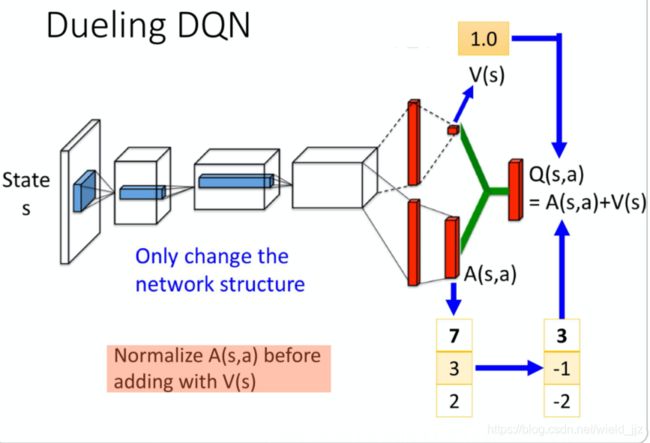
  加一个normalization，这个 normalization 做的事情就是把 7+3+2 加起来等于 12，12/3 = 4。然后把这边通通减掉4，变成 3, -1, 2。再把 3, -1, 2 加上 1.0，得到最后的 Q value。

这个 normalization 的 step 就是 network 的其中一部分，在 train 的时候，你从这边也是一路 back propagate回来的，只是 normalization 是没有参数的，它只是一个 normalization 的operation。把它可以放到 network 里面，跟 network 的其他部分 jointly trained，这样 A 就会有比较大的 constrain。这样 network 就会给它一些 benefit， 倾向于去 update V 的值，这个是 Dueling DQN。

优先经验回放 Prioritized Experience Replay

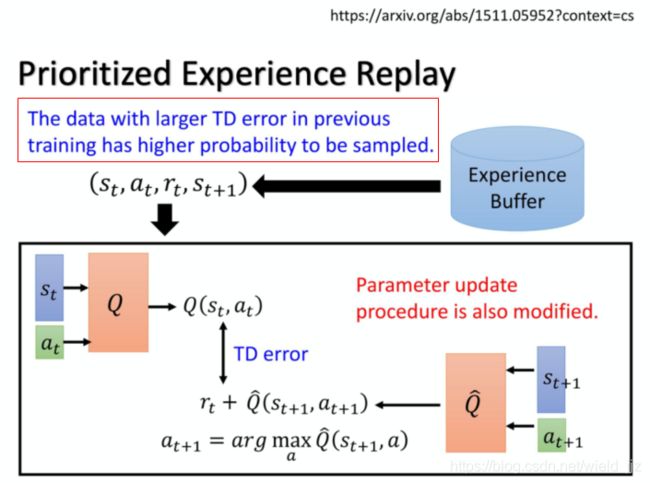
简单地说，在训练的过程中，对于在经验buffer里面的样本，那些具有更好的TD 误差的样本会有更高的概率被采样，这样可以加快训练速度。
在这个过程中，参数更新的过程也会有相应的更改。

Multi-step：Balance MC and TD

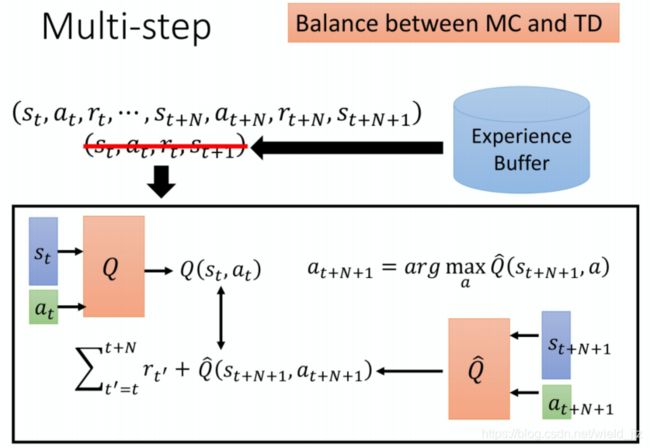
此处，模型需要学习多步累积起来的回报reward，也就是说将MC和TD进行了折中，同时引入了一个超参数，即累积reward的步长N。

• MC 和 TD 结合的好处和坏处
  好处：之前是只 sample 了一个 step， 只在某一个 step 得到的 真是的数据，接下来都是 Q value 估测出来的。现在 sample N 个 step 才估测 value，所以估测的部分所造成的影响就会比小。
  坏处：就跟 MC 的坏处一样，因为你的 r 比较多项，你把 N 项的 r 加起来，你的 variance 就会比较大。

但是你可以去调这个 N 的值，去在 variance 跟不精确的 Q 之间取得一个平衡。N 就是一个 hyper parameter，你要调这个 N 到底是多少，你是要多 sample 三步，还是多 sample 五步。

噪声网络 Noisy Net

Epsilon Greedy: 在行动上加噪声。即便给定相同的状态state，agent也有可能采取不同的行动，因此，实际上这里并没有真正意义上的policy。
Noisy Net: 在参数上加噪声。在每个episode开始时，在Q function的参数上引入噪声，但在每一个episode内，参数不会发生改变。给定同样的state，agent会采取同一个action。

Distributional Q-function

状态-行动价值函数 Q π ( s , a ) 是累积收益的期望值，也就是说是价值分布的均值。然而，有的时候不同的分布得到的均值可能一样，但我们并不知道实际的分布是什么。

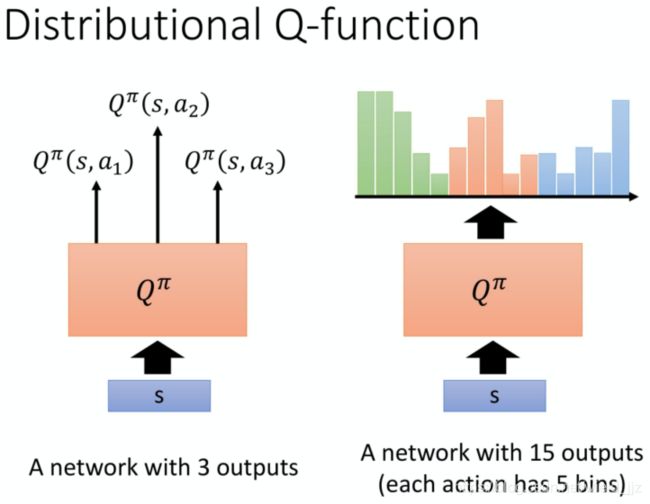
Distributional Q-function 认为可以输出Q值的分布，当具有相同的均值时，选择具有较小方差（风险）的那一个。但实际上，这个方法很难付诸实践。

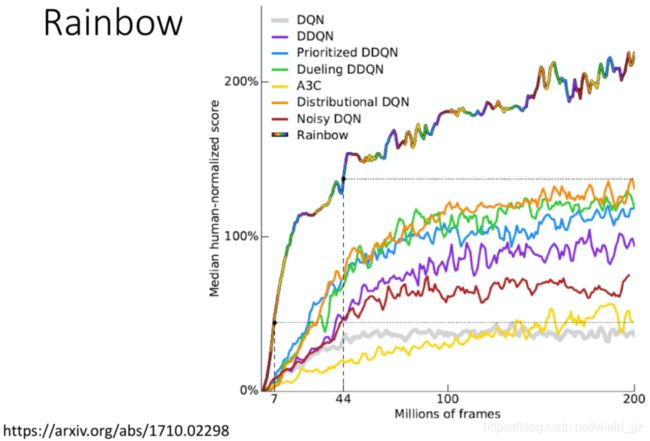
Rainbow

Rainbow： 也就是将我们这两节内容所有的七个tips综合起来的方法，7个方法分别包括：DQN、DDQN、Prioritized DDQN、Dueling DDQN、A3C、Distributional DQN、Noisy DQN，进而考察每一个方法的贡献度或者是否对于与环境的交互式正反馈的。

连续动作下的Q-learning

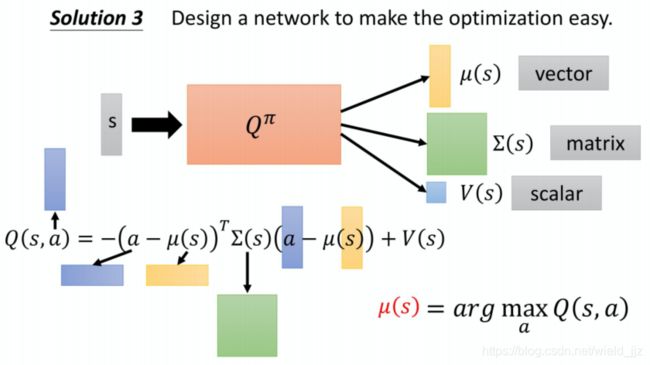
这里 ∑ 和 μ 是高斯分布的方差和均值，因此，该矩阵 ∑ 一定是正定的。
要让Q值较高，意味着要使得 ( a − μ ) ² 的值更小，也就是说 a=μ .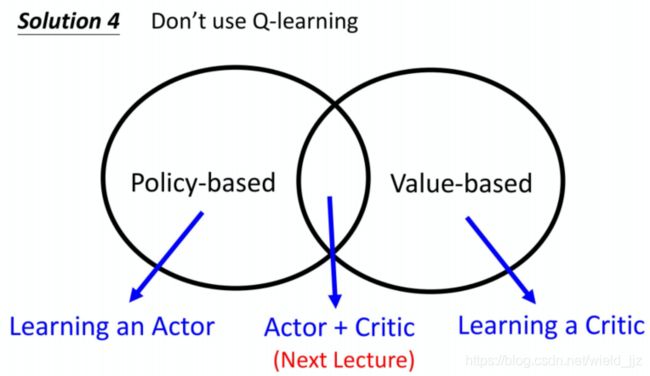

• Solution 1 ：采样一系列行动，看哪个行动会返回最大的Q值。
• Solution 2 ：使用梯度上升来解决这个优化问题（具有较高的计算成本）。
• Solution 3 ：设计一个网络来使得这个优化过程更简单。
• Solution 4 ：不使用 Q-learning，使用Actor-Critic 的方法。

Actor-Critic

基础知识

• A2C： Advantage Actor-Critic的缩写，一种Actor-Critic方法。
• A3C： Asynchronous（异步的）Advantage Actor-Critic的缩写，一种改进的Actor-Critic方法，通过异步的操作，进行RL模型训练的加速。
• Pathwise Derivative Policy Gradient： 其为使用 Q-learning 解 continuous action 的方法，也是一种 Actor-Critic 方法。其会对于actor提供value最大的action，而不仅仅是提供某一个action的好坏程度。

policy gradient

回顾一下policy gradient

• 当前时间的状态对过去没有影响，只与未来相关。所以我们的累计收益从当前时间开始计算，并且还要加上对未来的折扣；
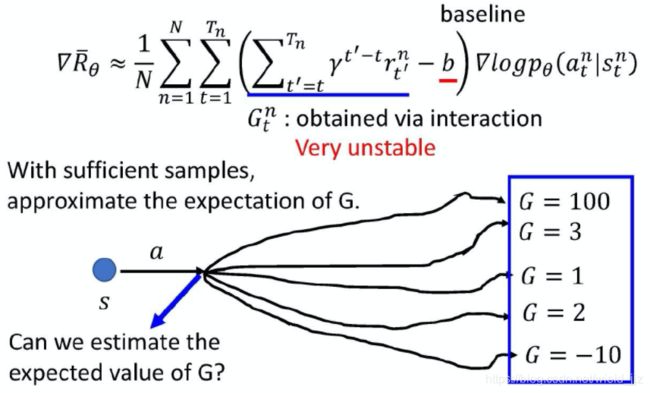
• 减去baseline，这个我们是希望累计收益可以有正有负，如果括号里面是正数，我们就要增加在这个state采取这个action的概率，相反，如果括号里面这一项是负数，就要减小在这个state采取这个action的概率。
• policy gradient的缺点就是这个G非常的不稳定，因为这里面集合了每一个单步reward的偏差，所以整体方差很大。

Q-learning

在回顾一下Q-learning

想要让训练过程更加稳定，并且通过直接估测G这个随机变量的期望值，就需要我们在 state s 采取 action a 的时候，直接用一个 network 去估测G 的期望值。如果这件事情是可行的，那之后训练的时候，就用期望值来代替sample 的值，这样会让训练变得比较稳定。

如何用期望值代替sample？
这边就需要引入 value based 的方法。value based 的方法就是 Q-learning。

• 状态价值函数 V^π(s)
• 状态-动作价值函数 Q^π(s,a)

Actor-Critic

在policy gradient的基础上，融合了Q-learning，形成Actor-Critic。

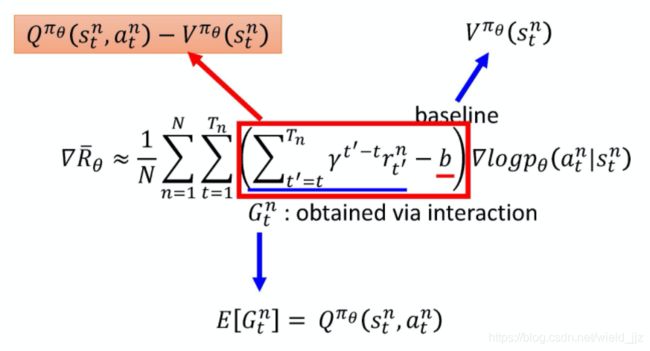
• 这里的G可以用G期望来代替，而G的期望就可以表示成Q；
• baseline就可以用V来代替，事实上V就是Q的期望，同样可以保证括号内的这一项有正有负。

如果你这么实现的话，有一个缺点是：你要 estimate 2 个 networks：Q-network 和 V-network，你估测不准的风险就变成两倍。所以我们何不只估测一个 network？

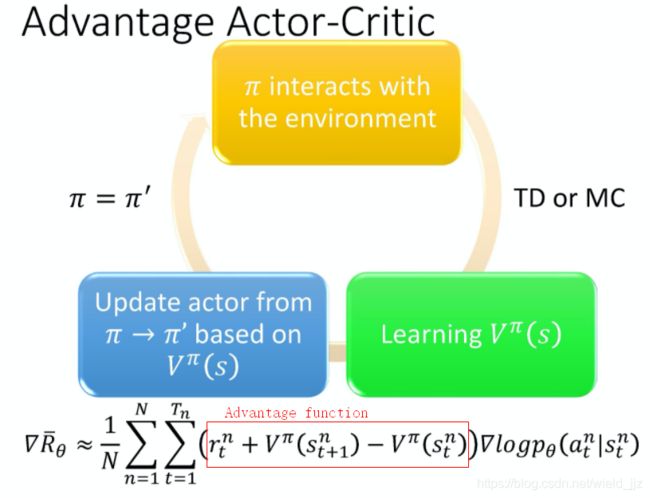
Advantage Actor-Critic

事实上在这个 Actor-Critic 方法里面，可以只估测 V 这个 network，我们可以用 V 的值来表示 Q 的值，即：

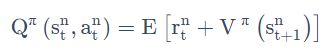
你在 state s 采取 action a，会得到 reward r，然后跳到 state s_t+1。但是你会得到什么样的 reward r，跳到什么样的 state s_t+1，它本身是有随机性的。所以要把右边这个式子，取期望值它才会等于 Q-function。

但是现在把期望去掉。把这个期望值去掉的好处就是不需要 estimate Q 了，只需要 estimate V 就够了。但这样你就引入了一个随机的东西 r ，它是有随机性的，它是一个 random variable。但是这个 random variable，相较于 accumulated reward G 可能还好，因为它是某一个 step 会得到的 reward，而 G 是所有未来会得到的 reward 的总和。

Tips

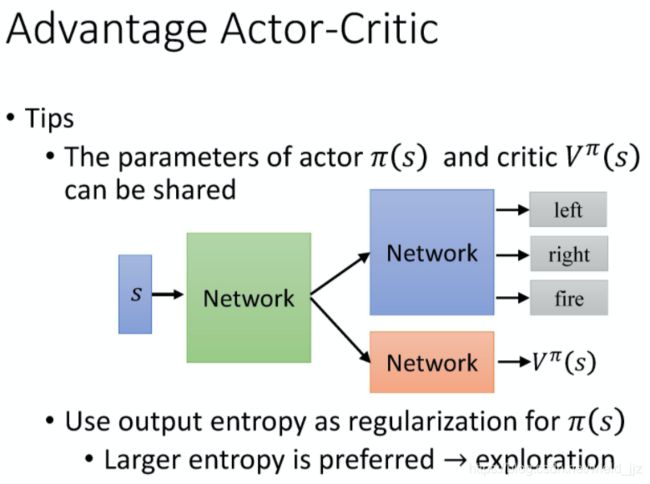
实现 Actor-Critic 的时候，有两个一定会用的 tip。

• 需要估计两个网络：V function 和 policy 的网络（也就是 actor）。这两个 网络，actor 和 critic 的输入都是 s，所以它们前面几个 layer，其实是可以 共享的。
• 需要 exploration 的机制。

A3C (Asynchronous Advantage Actor-Critic)

这个其实就是 Asynchronous(异步的) Advantage Actor-Critic。
效率提升是因为multi-workers
方法步骤：

1. 每个worker都会copy全局参数
2. 每个worker都与环境进行互动，并得到sample data
3. 计算梯度
4. 更新全局参数
   

Pathwise Derivative Policy Gradient

与GAN（生成对抗网路）的思想是一样的。
Q-learning对于连续的动作比较难处理，而Pathwise Derivative Policy Gradient 可以解决continuous action带来的问题。

对于最原始的actor-critic，critic只会告诉actor，某个行动是好的还是坏的。而这里引入的Pathwise Derivative Policy Gradient不仅仅会告诉actor某一个action的好坏，还会告诉actor应该采取哪一个action（使用以下训练出来的actor告知）

然后将这个actor 返回的action和state一起输入到一个固定的Q中，计算出来的Q值一定会增大，然后使用梯度上升更新actor，重复上述步骤。

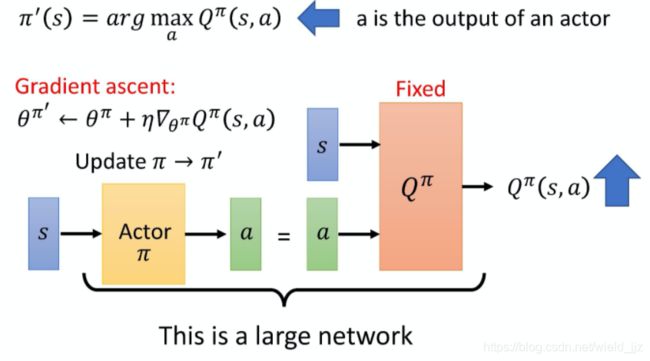
以上网络实际上是两个网络的叠加，类似于conditional GAN，其中actor是generator，Q是discriminator。

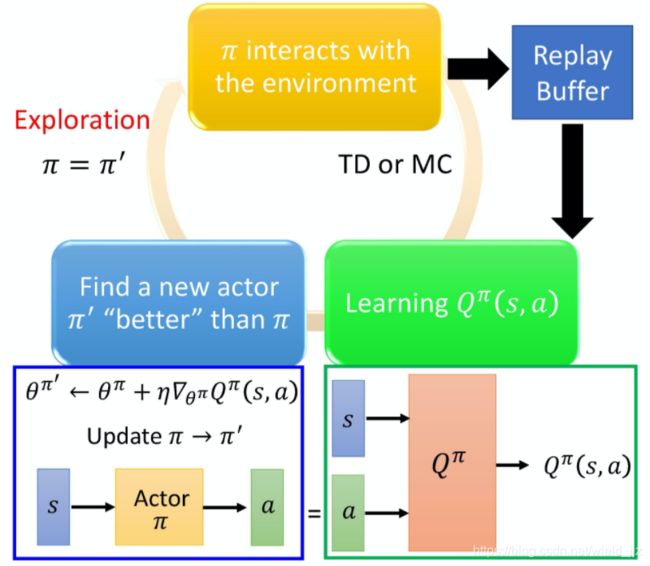
我们来看一下 pathwise derivative policy gradient 的算法。一开始你会有一个 actor π，它去跟环境互动，然后，你可能会要它去 estimate Q value 。estimate 完 Q value 以后，你就把 Q value 固定，只去 learn 一个 actor。假设这个 Q 估得是很准的，它知道在某一个 state 采取什么样的 action，会真的得到很大的 value。接下来就 learn 这个 actor，actor 在 given s 的时候，它采取了 a，可以让最后 Q-function 算出来的 value 越大越好。你用这个 criteria 去 update 你的 actor π。然后有新的 π 再去跟环境做互动，再estimate Q，再得到新的 π 去 maximize Q 的 output。本来在 Q-learning 里面，你用得上的技巧，在这边也几乎都用得上，比如说 replay buffer、exploration 等等。

Q-learning 到 Pathwise Derivative Policy Gradient 算法：

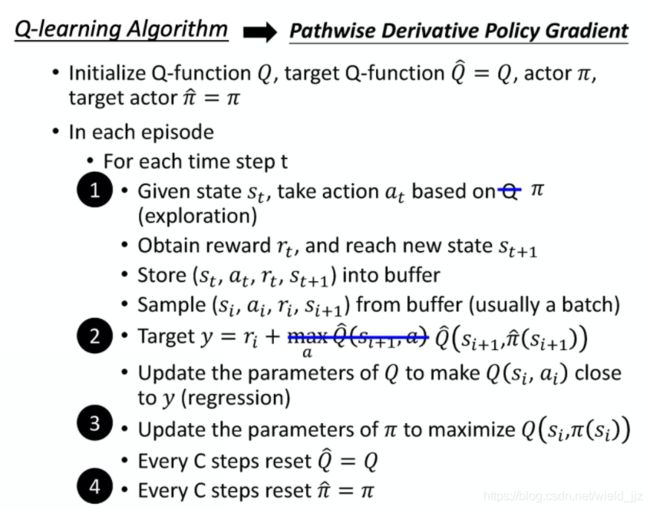
这里有四点改变：

1. 把 Q 换成 π，在Q-learning里面使用Q来决定在state s_t产生哪个action a_t，而在Pathwise Derivative Policy Gradient里面，直接学出来一个actor π直接告诉我们采取哪个action，这里就不需要求解arg max 的问题。
2. 本来这个地方是要计算在 s_i+1，根据你的 policy 采取某一个 action a 会得到多少的 Q value。现在是直接把s_i+1代到 policy π 里面，当给定s_i+1我们就可以知道采取哪一个 action 会给我们最大的 Q value。
3. 之前只要学Q，现在你多学一个π，学π 的目的就是为了 maximize Q-function这个跟 learn GAN 里面的 generator 的概念是一样的。
4. 原来是要把 target 的 Q network 取代掉，现在也要把 target policy 取代掉。

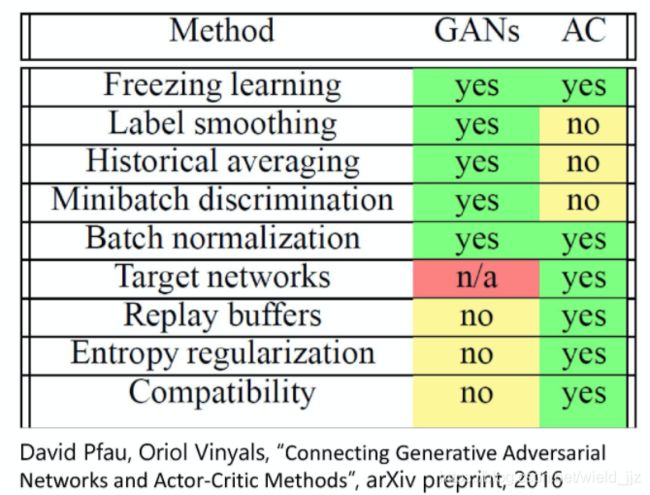
Connection with GAN

参考：
【笔记2-4】李宏毅深度强化学习笔记（四）Actor-Critic