m基于RFID和DBSCAN聚类的InSAR室内三维定位算法的matlab仿真
目录
1.算法描述
2.仿真效果预览
3.MATLAB核心程序
4.完整MATLAB
1.算法描述
许多室内应用需要有关物体的空间信息。示例应用程序包括项目查找,对象级别映射和在仓库或库中管理的大型对象。然而,使用802.11,可见光或声学的基于位置的服务的传统解决方案通常关注于用户,即人的位置而不是对象的位置。RFID技术通过集成RFID标签,可以在日常生活中识别和定位物体。标签反向散射的RF信号包括关于对象环境的许多信息,这些信息可用于导出对象的空间信息。为此,Malla等人。
在本文中,我们提出了一种3D定位方案3DinSAR,用于通过分析标签反向散射载波的相位特征为室内RFID应用提供空间信息的对象。为了降低复杂性并最大限度地减少将我们的解决方案集成到现有系统的工作量,我们的方法不在环境中使用参考标签或额外的读取器天线。我们的3D定位方案仅使用一个可移动天线实现。它适用于便携式阅读器和运输车辆。
我们的方法利用干涉合成孔径雷达(InSAR)高度确定理论。它扩展了现有的2D全息图定位方案。我们不是遍历所有耗时且因此效率不高的空间像素,而是通过使用与波路差异和标签高度相关的空间域相位差作为附加信息,将幼稚全息图定位扩展为3D方案。我们还考虑基于密度的空间聚类方法来选择最可能的位置以提高准确性。
我们使用COTS组件实施我们的系统并在大学的办公环境中对其进行评估。使用真实硬件,我们表明我们的系统实现了定位精度,空间中位误差为0.24 m。我们的主要贡献是我们是第一个在没有任何参考标签和额外设备的情况下为基于3D RFID的本地化系统呈现真实世界的结果。
我们设置的测试场景如下:
整个算法的基本流程是这样的:
第一、测量相位偏移
第二、计算二维全息图
第三、
![]()
我们根据这个公式,得到xt ,即论文中介绍的
第四、
第五、
然后上面的四个大的步骤,我们得到了xt,yt,zt的一堆数据点,比较散的一堆点。
此时,我们使用
![]()
这个聚类算法,分别计算xt,yt,zt中对应的最有可能的目标点。
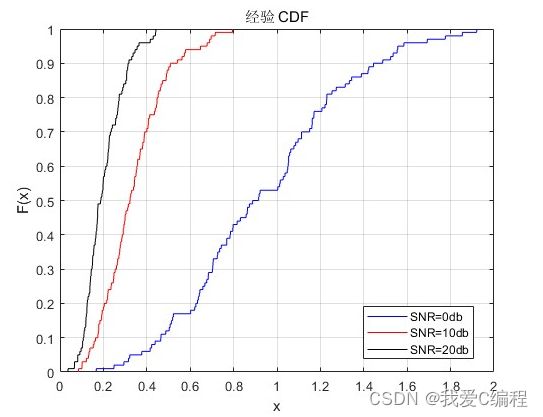
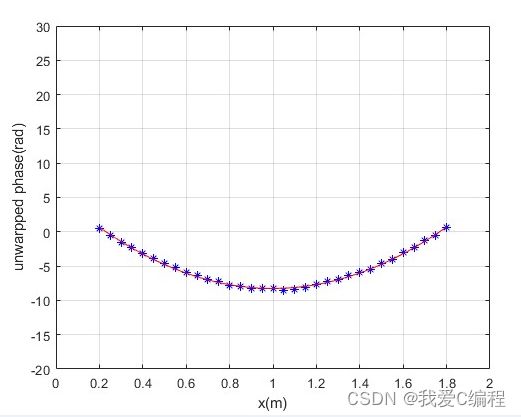
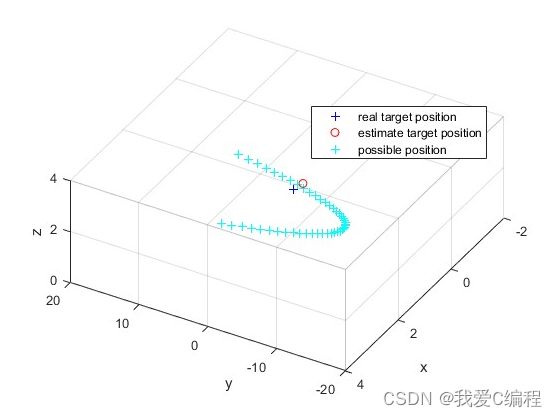
2.仿真效果预览
matlab2022a仿真结果如下:
3.MATLAB核心程序
for sel = 1:6;
pos_reader=[0.2 0 0.63];
N=50;
d=zeros(1,N);
for i=1:N;
pos_reader(1)=0.2+0.02*(i-1);
d(i)=norm(pos_tag(sel,:)-pos_reader); %标签与天线之间的距离
end
C = 3e8; %propagation speed
f_c = 920625000; %carrier frequency
lambda = C/f_c; %wavelength
phi = [];
std = 5;
phi_ii = mod(4*pi*d/lambda+randn(1,N)/2,2*pi); %the measured phase offset
%WxL grid
[w,l] = meshgrid(0.05:0.01:3,0.05:0.01:3);
% X = [w(:) l(:)];
P = zeros(size(w));
for n=1:N
pos_reader(1) = 0.2+0.02*(n-1);
%网格点与天线的距离
d_2 = sqrt((w-pos_tag(sel,1)).^2+(l-pos_tag(sel,2)).^2);
P_1 = exp((mod(4*pi/lambda.*d_2,2*pi)-phi_ii(n))); %RF holographic image
P = P+real(P_1 );
end
p = 0;
M = length(w);
idx=0;
x_t=[];
y_t=[];
[x,y]=find(P==min(min(P)));
x_t=w(x,y);
y_t=l(x,y);
H=0.63;
X=[];
Y=[];
Z=[];
R_n=0.8;
d_yz=sqrt((pos_tag(sel,2)-pos_reader(2))^2+(pos_tag(sel,3)-pos_reader(3))^2);
STD=5;
phi_yz=[];
for j=1:STD
phi_j=mod(4*pi*d_yz/lambda+randn(1)/2,2*pi);
phi_yz=[phi_yz phi_j];
end
phi_yz=mean(phi_yz); %利用InSAR时天线An测得相位
for B=0.01:0.01:0.34 %改变天线高度
k=fix(2*B/lambda); %k is integer related to the antenna and tag positions
for i=-k:1:k
D=sqrt((pos_tag(sel,2)-pos_reader(2))^2+(pos_tag(sel,3)-pos_reader(3)-B)^2); %天线高度为H+B时与标签距离
phi_B=mod(4*pi*D/lambda,2*pi); %天线在z轴上的位置为H+B时测得的相位
Delta_phi=phi_yz-phi_B+2*k*pi; %相位差
Delta_Rn=Delta_phi*lambda/(4*pi); %天线高度改变前后与标签距离的差值
R_n1=R_n+Delta_Rn; %天线高度为H+B时与标签的距离
cosbeta=(R_n^2+B^2-Delta_Rn^2)/(2*R_n*B);
z_t=H+B*cosbeta;
X=[X x_t];
Y=[Y y_t];
Z=[Z z_t];
end
end
data1=[X;Y];
data2=[Y;Z];
data3=[X;Z];
[k,C1] = dbscan(data1);
[k,C2] = dbscan(data2);
[k,C3] = dbscan(data3);
X1=mean(C1(1,:));
Y1=mean(C1(2,:));
Y2=mean(C2(1,:));
Z2=mean(C3(2,:));
X3=mean(C1(1,:));
Z3=mean(C1(2,:));
X_(sel)=(X1+X3)/2;
Y_(sel)=(Y1+Y2)/2;
Z_(sel)=(Z2+Z3)/2;
end
01_179m4.完整MATLAB
V