GWmodel | 地理加权模型(Ⅱ-2):如何查看地理加权回归的显著性
《地理加权模型》系列自推出来,深受各位读者喜爱。前几天有读者问:使用gwr()等函数运行模型后,怎么去查看它里面的信息呢?比如如何看变量系数的显著性。本篇就来介绍如何在R语言中去查看GWR模型的输出结果。
对于一般模型如线型模型来说,使用summary()函数就能得到大部分想要的结果,如回归系数、标准误、值、R2等。
但是,GWR模型每个变量在每个样本点都有一个估计系数,以及对应的标准误、值,即使全部输出出来也非常不直观,因此一般使用地图的方式来展示GWR的结果。
模型输出结果的数据结构是list,它包含的内容可以在对应函数帮助文档的value部分查看。
spgwr工具包gwr()函数:

GWmodel工具包gwr.basic()函数:

从上面可以看出,无论是spgwr工具包,还是GWmodel工具包,其模型的主要信息都存在于元素SDF的data部分。
下面使用model.1表示spgwr工具包的输出结果,model.2表示GWmodel的输出结果。具体模型见文末。
以model.2为例,找到它的SDF模块:
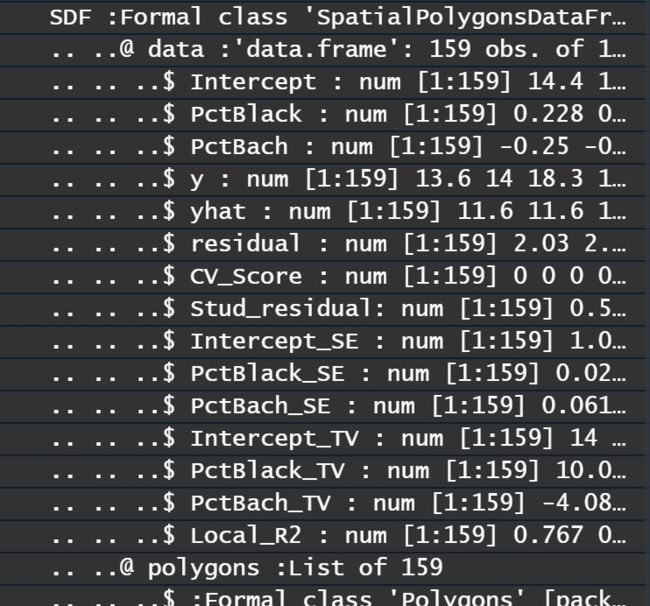
model.2$SDF@data上行代码就可以将模型结果以数据框(data.frame)的形式输出出来,包含的线性如下:
colnames(model.2$SDF@data)
## [1] "Intercept" "PctBlack" "PctBach" "PctEld"
## [5] "y" "yhat" "residual" "CV_Score"
## [9] "Stud_residual" "Intercept_SE" "PctBlack_SE" "PctBach_SE"
## [13] "PctEld_SE" "Intercept_TV" "PctBlack_TV" "PctBach_TV"
## [17] "PctEld_TV" "Local_R2"可视化局部R2的结果:
dta.sf <- st_as_sf(dta)
dta.sf$R2 <- model.2$SDF@data$Local_R2
plot(dta.sf["R2"])
t统计量可以表示显著性,当t的绝对值大于1.96时表示在95%的置信区间下显著。
dta.sf$t <- model.2$SDF@data$PctEld_TV
plot(dta.sf["t"])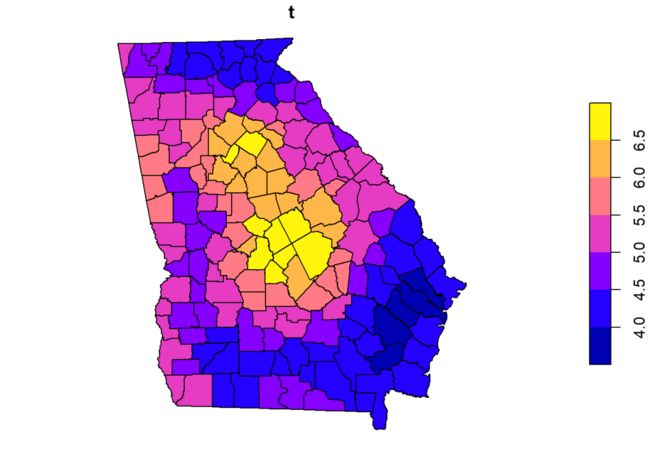
model.1的内容在默认情况下不包含t统计量或其他表示显著性的指标,如果需要可以在调用gwr()函数时设置参数se.fit = TRUE,表示输出估计系数的标准误,而系数与标准误之比即为t统计量。
但是在本例中,运行model.1会出现以下警告信息,并且结果中标准误的信息全部是NA,因此还是推荐使用GWmodel工具包。
standard errors set to NA, normalised RSS not available
各位读者还可以使用summary()函数和print()函数分别查看GWR模型的结果,由于输出内容较长,这里不再展示。
summary(model.1)
summary(model.1)
print(model.1)
print(model.2)以下为模型信息。
示例数据和模型表达式:
library(GWmodel)
library(spgwr)
library(sf)
library(sp)
library(tidyverse)
data(Georgia)
data(GeorgiaCounties)
Gedu.df$AreaKey <- factor(Gedu.df$AreaKey)
dta <- Gedu.counties %>%
st_as_sf() %>%
left_join(Gedu.df, by = c("AREAKEY" = "AreaKey")) %>%
as("Spatial")
formula <- PctPov ~ PctBlack + PctBach + PctEld运行模型:
model.1 <- gwr(formula, data = dta,
adapt = 22/159,
gweight = gwr.Gauss,
se.fit = T)
model.2 <- gwr.basic(formula, data = dta,
bw = 22,
adaptive = T,
kernel = "gaussian")