李沐动手学深度学习V2-LeNet模型和代码实现
1. LeNet
LeNet是最早发布的卷积神经网络之一,因其在计算机视觉任务中的高效性能而受到广泛关注。 这个模型是由AT&T贝尔实验室的研究员Yann LeCun在1989年提出的(并以其命名),目的是识别图像中的手写数字。
1.1 LeNet架构:
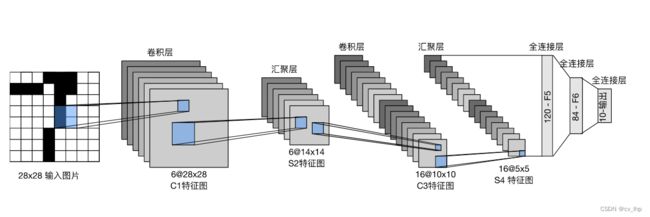
总体来看,LeNet由两个部分组成:卷积块(有两个卷积层组成)和全连接块(由三个全连接层组成),架构如下图所示。
**每个卷积块中的基本单元是一个卷积层、一个sigmoid激活函数和平均汇聚层。请注意,虽然ReLU和最大汇聚层更有效,**但它们在20世纪90年代还没有出现。**每个卷积层使用 5×5 卷积核和一个sigmoid激活函数。这些层将输入映射到多个二维特征输出,并且同时增加通道的数量。**第一卷积层有6个输出通道,而第二个卷积层有16个输出通道。每个 2×2 池操作通过空间下采样将维数减少4倍。卷积的输出形状由批量大小、通道数、高度、宽度决定。
为了将卷积块的输出传递给全连接稠密块,我们必须在小批量中展平每个样本。换言之,**我们将这个四维输入转换成全连接层所期望的二维输入。**这里的二维表示的第一个维度索引小批量中的样本,第二个维度给出每个样本的平面向量特征表示。LeNet的全连接稠密块有三个全连接层,分别有120、84和10个输出。因为我们在执行分类任务,所以输出层的10维对应于最后输出结果的分类数量。
1.2 LeNet模型定义
通过将一个大小为 28×28 的单通道(黑白)图像通过LeNet。通过在每一层打印输出的形状,我们可以检查模型,以确保其操作与我们期望的输出形状大小一致,如下图模型每层结构所示。
在整个卷积块中,与上一层相比,每一层特征的高度和宽度都减小了。 第一个卷积层使用2个像素的填充,来补偿 5×5 卷积核导致的特征减少。 相反,第二个卷积层没有填充,因此高度和宽度都减少了4个像素。 随着层叠的上升,通道的数量从输入时的1个,增加到第一个卷积层之后的6个,再到第二个卷积层之后的16个。 同时,每个汇聚层的高度和宽度都减半。最后,每个全连接层减少维数,最终输出一个维数与结果分类数相匹配的输出。

LeNet模型定义代码:
import d2l.torch
import torch
from torch import nn
#定义LeNet网络
LeNet = nn.Sequential(nn.Conv2d(in_channels=1,out_channels=6,kernel_size=5,padding=2,stride=1),nn.Sigmoid(),#加上padding后输入输出尺寸大小不变
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Conv2d(in_channels=6,out_channels=16,kernel_size=5,padding=0,stride=1),nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Flatten(),#铺平
nn.Linear(in_features=16*5*5,out_features=120),nn.Sigmoid(),
nn.Linear(in_features=120,out_features=84),nn.Sigmoid(),
nn.Linear(in_features=84,out_features=10)) #对LeNet原始模型做了一点小改动,去掉了最后一层的高斯激活。除此之外,这个网络与最初的LeNet-5一致。
print(LeNet)
X = torch.randn(size=(1,1,28,28))
for layer in LeNet:
X = layer(X)
print(layer.__class__.__name__,'output layer shape:\t',X.shape)#打印每一层的信息
输出结果:
Sequential(
(0): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(1): Sigmoid()
(2): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(4): Sigmoid()
(5): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Flatten(start_dim=1, end_dim=-1)
(7): Linear(in_features=400, out_features=120, bias=True)
(8): Sigmoid()
(9): Linear(in_features=120, out_features=84, bias=True)
(10): Sigmoid()
(11): Linear(in_features=84, out_features=10, bias=True)
)
Conv2d output layer shape: torch.Size([1, 6, 28, 28])
Sigmoid output layer shape: torch.Size([1, 6, 28, 28])
MaxPool2d output layer shape: torch.Size([1, 6, 14, 14])
Conv2d output layer shape: torch.Size([1, 16, 10, 10])
Sigmoid output layer shape: torch.Size([1, 16, 10, 10])
MaxPool2d output layer shape: torch.Size([1, 16, 5, 5])
Flatten output layer shape: torch.Size([1, 400])
Linear output layer shape: torch.Size([1, 120])
Sigmoid output layer shape: torch.Size([1, 120])
Linear output layer shape: torch.Size([1, 84])
Sigmoid output layer shape: torch.Size([1, 84])
Linear output layer shape: torch.Size([1, 10])
1.3 模型训练
使用Xavier_uniform分布随机初始化网络模型参数,与全连接层一样,使用交叉熵损失函数和小批量随机梯度下降。
模型训练代码如下:
#计算网络在测试数据集上面的准确率
#由于完整的测试数据集位于内存中,因此在模型使用GPU预测测试数据集之前,我们需要将其复制到显存中。
def evaluate_accuracy_gpu(net,data_iter,device=None):
if isinstance(net,nn.Module):
net.eval() #网络用于测试数据
if not device:
device = next(iter(net.parameters())).device #如果没有指定device设备,device设备则使用第一层网络参数的设备
accumulator = d2l.torch.Accumulator(2) #累加器里面包含两个元素
for X,y in data_iter:
if isinstance(X,list):
X = [x.to(device) for x in X] #X为list类型时,需要加X里面每个元素都复制到device设备上面来
else:
X = X.to(device)
y = y.to(device)
accumulator.add(d2l.torch.accuracy(net(X),y),y.numel()) #累加器第一个元素为在每一个batch_size中预测准确的个数,第二个元素为每一个batch_size中样本总数目,然后依次循环累加,得到测试数据集上面预测准确的总数目,以及数据集总数目
return accumulator[0]/accumulator[1] #算出模型预测准确率
batch_size = 256
train_iter,test_iter = d2l.torch.load_data_fashion_mnist(batch_size=batch_size)
def train_LeNet(net,train_iter,test_iter,lr,num_epochs,device):
def init_weights(m):#手动初始化模型参数
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight) #使用xavier_uniform分布初始化参数
net.apply(init_weights)
net.to(device)#将模型复制到gpu上面
loss = nn.CrossEntropyLoss() #定义loss
optim = torch.optim.SGD(net.parameters(),lr=lr) #定义优化器
animator = d2l.torch.Animator(xlabel='epoch',xlim=[1,num_epochs],legend=['train_loss','train_acc','test_acc'])
timer = d2l.torch.Timer()
num_batches = len(train_iter)
for epoch in range(num_epochs):
net.train()#模型开始训练,需要放在第一层循环里面,因为后面evaluate_accuracy_gpu()函数里面有net.eval(),将模型改变为测试状态,因此需要在每一个循环epoch后面手动再加上模型开始处于训练状态
accumulator = d2l.torch.Accumulator(3) #累加器
for i,(X,y) in enumerate(train_iter):
timer.start()
optim.zero_grad()
X = X.to(device)#将X复制到gpu上面
y = y.to(device) #将y复制到gpu上面
y_hat = net(X) #得到模型训练后的输出标签y_hat
l = loss(y_hat,y)#计算每一个batch_size的loss
l.backward() #计算梯度
optim.step() #使用优化器更新模型参数
with torch.no_grad():#不需要模型梯度
accumulator.add(l*X.shape[0],d2l.torch.accuracy(y_hat,y),X.shape[0])
timer.stop()
train_loss = accumulator[0]/accumulator[2] #从累加器里面获得所有训练集的loss之和
train_acc = accumulator[1]/accumulator[2] #从累加器里面获得所有训练集的准确数之和
if (i+1) % (num_batches // 5) == 0 or i == num_batches-1:
animator.add(epoch+(i+1)/num_batches,(train_loss,train_acc,None))
test_accuracy = evaluate_accuracy_gpu(net,test_iter) #每次训练完一个epoch后的模型用于测试数据集上面计算测试精确度
animator.add(epoch+1,(None,None,test_accuracy))
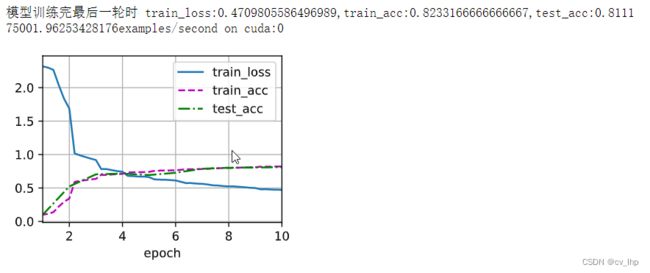
print(f'模型训练完最后一轮时 train_loss:{train_loss},train_acc:{train_acc},test_acc:{test_accuracy}')
print(f'{num_epochs*accumulator[2]/timer.sum()}examples/second on {str(device)}')#打印出模型每秒能处理多少个样本数
lr,num_epochs= 0.9,10
train_LeNet(net=LeNet,train_iter=train_iter,test_iter=test_iter,lr=lr,num_epochs=num_epochs,device=d2l.torch.try_gpu())
'''
输出结果:
模型训练完最后一轮时 train_loss:0.4322478462855021,train_acc:0.8396666666666667,test_acc:0.8163
55954.65804440994examples/second on cuda:0
'''
1.4 小结
- 卷积神经网络(LeNet)是一类使用卷积层的网络。
- 在卷积神经网络中,我们组合使用卷积层、非线性激活函数和汇聚层(池化层)。
- 为了构造高性能的(更大更深)卷积神经网络,我们通常对卷积层进行排列,逐渐降低其表示的空间分辨率(输出尺寸形状(高和宽)大小),同时增加通道数。
- 在传统的卷积神经网络中,卷积块编码得到的表征在输出之前需由一个或多个全连接层进行处理(通常需要由一个Flatten()层将卷积块的输出铺平,然后再作为输入到全连接层中。
- LeNet是最早发布的卷积神经网络之一。
2.全部源代码
2.1 原始LeNet模型源代码(模型使用AvgPool2d池化层,Sigmoid()非线性激活函数,lr =0.9学习率,epochs = 10轮)
#原始LeNet源代码
import d2l.torch
import torch
from torch import nn
#定义LeNet网络
LeNet = nn.Sequential(nn.Conv2d(in_channels=1,out_channels=6,kernel_size=5,padding=2,stride=1),nn.Sigmoid(),#加上padding后输入输出尺寸大小不变
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Conv2d(in_channels=6,out_channels=16,kernel_size=5,padding=0,stride=1),nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2,stride=2),
nn.Flatten(),#铺平
nn.Linear(in_features=16*5*5,out_features=120),nn.Sigmoid(),
nn.Linear(in_features=120,out_features=84),nn.Sigmoid(),
nn.Linear(in_features=84,out_features=10)) #对LeNet原始模型做了一点小改动,去掉了最后一层的高斯激活。除此之外,这个网络与最初的LeNet-5一致。
print(LeNet)
X = torch.randn(size=(1,1,28,28))
for layer in LeNet:
X = layer(X)
print(layer.__class__.__name__,'output layer shape:\t',X.shape)#打印每一层的信息
#计算网络在测试数据集上面的准确率
#由于完整的测试数据集位于内存中,因此在模型使用GPU预测测试数据集之前,我们需要将其复制到显存中。
def evaluate_accuracy_gpu(net,data_iter,device=None):
if isinstance(net,nn.Module):
net.eval() #网络用于测试数据
if not device:
device = next(iter(net.parameters())).device #如果没有指定device设备,device设备则使用第一层网络参数的设备
accumulator = d2l.torch.Accumulator(2) #累加器里面包含两个元素
for X,y in data_iter:
if isinstance(X,list):
X = [x.to(device) for x in X] #X为list类型时,需要加X里面每个元素都复制到device设备上面来
else:
X = X.to(device)
y = y.to(device)
accumulator.add(d2l.torch.accuracy(net(X),y),y.numel()) #累加器第一个元素为在每一个batch_size中预测准确的个数,第二个元素为每一个batch_size中样本总数目,然后依次循环累加,得到测试数据集上面预测准确的总数目,以及数据集总数目
return accumulator[0]/accumulator[1] #算出模型预测准确率
batch_size = 256
train_iter,test_iter = d2l.torch.load_data_fashion_mnist(batch_size=batch_size)
def train_LeNet(net,train_iter,test_iter,lr,num_epochs,device):
def init_weights(m):#手动初始化模型参数
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight) #使用xavier_uniform分布初始化参数
net.apply(init_weights)
net.to(device)#将模型复制到gpu上面
loss = nn.CrossEntropyLoss() #定义loss
optim = torch.optim.SGD(net.parameters(),lr=lr) #定义优化器
animator = d2l.torch.Animator(xlabel='epoch',xlim=[1,num_epochs],legend=['train_loss','train_acc','test_acc'])
timer = d2l.torch.Timer()
num_batches = len(train_iter)
for epoch in range(num_epochs):
net.train()#模型开始训练,需要放在第一层循环里面,因为后面evaluate_accuracy_gpu()函数里面有net.eval(),将模型改变为测试状态,因此需要在每一个循环epoch后面手动再加上模型开始处于训练状态
accumulator = d2l.torch.Accumulator(3) #累加器
for i,(X,y) in enumerate(train_iter):
timer.start()
optim.zero_grad()
X = X.to(device)#将X复制到gpu上面
y = y.to(device) #将y复制到gpu上面
y_hat = net(X) #得到模型训练后的输出标签y_hat
l = loss(y_hat,y)#计算每一个batch_size的loss
l.backward() #计算梯度
optim.step() #使用优化器更新模型参数
with torch.no_grad():#不需要模型梯度
accumulator.add(l*X.shape[0],d2l.torch.accuracy(y_hat,y),X.shape[0])
timer.stop()
train_loss = accumulator[0]/accumulator[2] #从累加器里面获得所有训练集的loss之和
train_acc = accumulator[1]/accumulator[2] #从累加器里面获得所有训练集的准确数之和
if (i+1) % (num_batches // 5) == 0 or i == num_batches-1:
animator.add(epoch+(i+1)/num_batches,(train_loss,train_acc,None))
test_accuracy = evaluate_accuracy_gpu(net,test_iter) #每次训练完一个epoch后的模型用于测试数据集上面计算测试精确度
animator.add(epoch+1,(None,None,test_accuracy))
print(f'模型训练完最后一轮时 train_loss:{train_loss},train_acc:{train_acc},test_acc:{test_accuracy}')
print(f'{num_epochs*accumulator[2]/timer.sum()}examples/second on {str(device)}')#打印出模型每秒能处理多少个样本数
lr,num_epochs= 0.9,10
train_LeNet(net=LeNet,train_iter=train_iter,test_iter=test_iter,lr=lr,num_epochs=num_epochs,device=d2l.torch.try_gpu())
2.2 改进后的LeNet模型(模型使用MaxPool2d池化层,ReLU()非线性激活函数,lr =0.03学习率,epochs = 150轮,batch_size = 256)
#改进后的LeNet代码
import d2l.torch
import torch
from torch import nn
#定义LeNet网络
LeNet = nn.Sequential(nn.Conv2d(in_channels=1,out_channels=6,kernel_size=5,padding=2,stride=1),nn.ReLU(),#加上padding后输入输出尺寸大小不变
nn.MaxPool2d(kernel_size=2,stride=2),
nn.Conv2d(in_channels=6,out_channels=16,kernel_size=5,padding=0,stride=1),nn.ReLU(),
nn.MaxPool2d(kernel_size=2,stride=2),
nn.Flatten(),#铺平
nn.Linear(in_features=16*5*5,out_features=120),nn.ReLU(),
nn.Linear(in_features=120,out_features=84),nn.ReLU(),
nn.Linear(in_features=84,out_features=10))
print(LeNet)
X = torch.randn(size=(1,1,28,28))
for layer in LeNet:
X = layer(X)
print(layer.__class__.__name__,'output layer shape:\t',X.shape)#打印每一层的信息
#计算网络在测试数据集上面的准确率
def evaluate_accuracy_gpu(net,data_iter,device=None):
if isinstance(net,nn.Module):
net.eval() #网络用于测试数据
if not device:
device = next(iter(net.parameters())).device #如果没有指定device设备,device设备则使用第一层网络参数的设备
accumulator = d2l.torch.Accumulator(2) #累加器里面包含两个元素
for X,y in data_iter:
if isinstance(X,list):
X = [x.to(device) for x in X] #X为list类型时,需要加X里面每个元素都复制到device设备上面来
else:
X = X.to(device)
y = y.to(device)
accumulator.add(d2l.torch.accuracy(net(X),y),y.numel()) #累加器第一个元素为在每一个batch_size中预测准确的个数,第二个元素为每一个batch_size中样本总数目,然后依次循环累加,得到测试数据集上面预测准确的总数目,以及数据集总数目
return accumulator[0]/accumulator[1] #算出模型预测准确率
batch_size = 256
train_iter,test_iter = d2l.torch.load_data_fashion_mnist(batch_size=batch_size)
def train_LeNet(net,train_iter,test_iter,lr,num_epochs,device):
def init_weights(m):
if type(m) == nn.Linear or type(m) == nn.Conv2d:
nn.init.xavier_uniform_(m.weight)
net.apply(init_weights)
net.to(device)
loss = nn.CrossEntropyLoss()
optim = torch.optim.SGD(net.parameters(),lr=lr)
animator = d2l.torch.Animator(xlabel='epoch',xlim=[1,num_epochs],legend=['train_loss','train_acc','test_acc'])
timer = d2l.torch.Timer()
num_batches = len(train_iter)
for epoch in range(num_epochs):
net.train()
accumulator = d2l.torch.Accumulator(3)
for i,(X,y) in enumerate(train_iter):
timer.start()
optim.zero_grad()
X = X.to(device)
y = y.to(device)
y_hat = net(X)
l = loss(y_hat,y)
l.backward()
optim.step()
with torch.no_grad():
accumulator.add(l*X.shape[0],d2l.torch.accuracy(y_hat,y),X.shape[0])
timer.stop()
train_loss = accumulator[0]/accumulator[2]
train_acc = accumulator[1]/accumulator[2]
if (i+1) % (num_batches // 5) == 0 or i == num_batches-1:
animator.add(epoch+(i+1)/num_batches,(train_loss,train_acc,None))
test_accuracy = evaluate_accuracy_gpu(net,test_iter,device)
animator.add(epoch+1,(None,None,test_accuracy))
print(f'模型训练完最后一轮时 train_loss:{train_loss},train_acc:{train_acc},test_acc:{test_accuracy}')
print(f'{num_epochs*accumulator[2]/timer.sum()}examples/second on {str(device)}')
lr,num_epochs= 0.03,150
train_LeNet(net=LeNet,train_iter=train_iter,test_iter=test_iter,lr=lr,num_epochs=num_epochs,device=d2l.torch.try_gpu())
改进后的LeNet模型训练结果输出如下图所示:
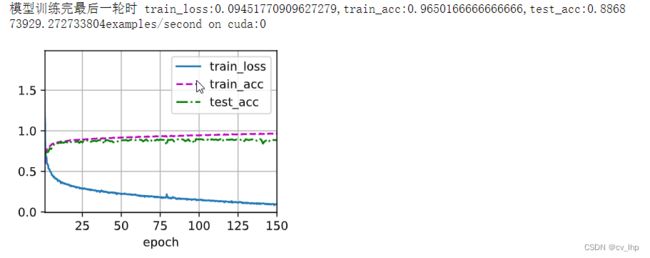
从上面两个图可以看出,ReLU非线性函数和最大汇聚层(池化层)对于卷积神经网络更有效