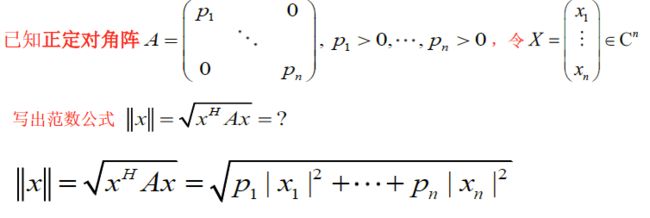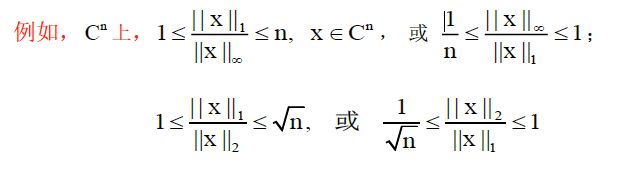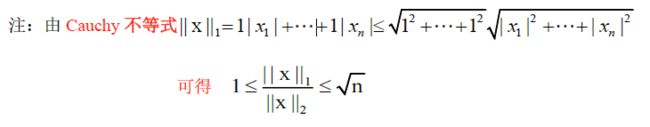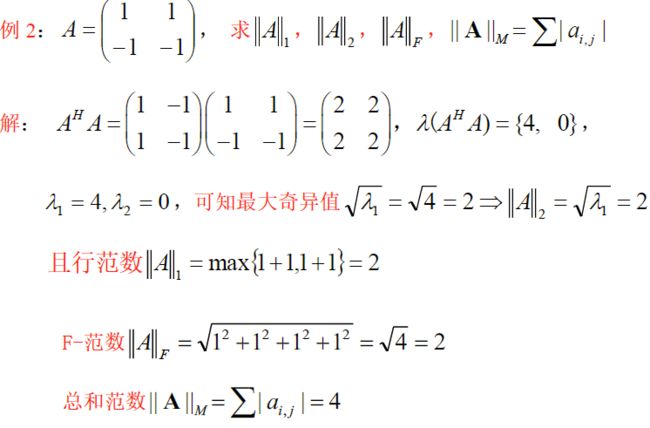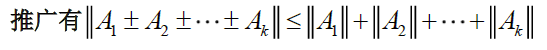【矩阵论】6. 范数理论——基本概念——向量范数与矩阵范数

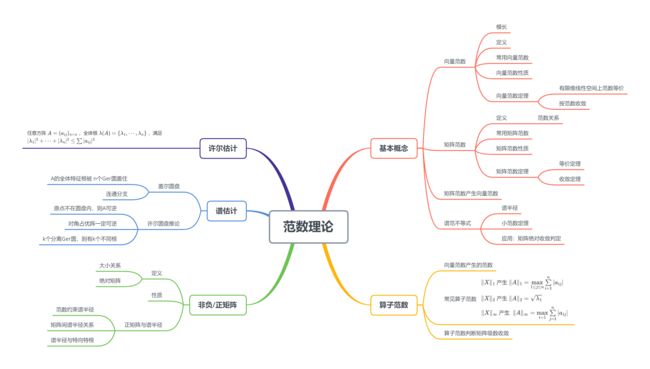
6.1 基本概念

6.1.1 向量范数

a. 模长（二范数）

C n 中向量 X = ( x 1 x 2 ⋮ x n ) 的模长为 ∣ X ∣ = ( X , X ) = t r ( A H A ) = ∣ x 1 ∣ 2 + ∣ x 2 ∣ 2 + ⋯ + ∣ x n ∣ 2 C^n中向量 X=\left( \begin{matrix} x_1\\x_2\\\vdots\\x_n \end{matrix} \right)的模长为 \vert X\vert=\sqrt{(X,X)}=\sqrt{tr(A^HA)} =\sqrt{\vert x_1\vert^2+\vert x_2\vert^2+\cdots+\vert x_n\vert^2 } Cn中向量X= ​x1​x2​⋮xn​​ ​的模长为∣X∣=(X,X) ​=tr(AHA) ​=∣x1​∣2+∣x2​∣2+⋯+∣xn​∣2 ​

• 正性：$|X|>0$

• 齐性：$|kX|=|k||X|$

  $|-x|=|x|$

• 三角性：$|x+y|\le |x|+|y|$

  $\left||x|-|y|\right|\le |x-y|$

内积空间引入模长

任一内积空间W都可引入向量z长度(模长) $|\alpha |=\sqrt{(\alpha ,\alpha )},\alpha \in W$

满足柯西-施瓦茨不等式 $|\alpha +\beta |\le \sqrt{(\alpha ,\alpha )}\sqrt{(\beta ,\beta )}=|\alpha ||\beta |$

• 三角性：$|\alpha +\beta |\le |\alpha |+|\beta |$
• 正性
• 齐性

二维空间引入模长范数

令矩阵空间 $V=C^{m,n}$ ，$A=(a_{ij})，B=(b_{ij})\in C^{m,n}$ ，
$$(A,B)=B^{H}A=tr(B^{H}A)=tr(A^{H}B)=\sum (|a_{ij}|\overline{|b_{ij}|})$$
规定 $\Vert A\Vert =\sqrt{(A,A)}=\sqrt{tr(A^{H}A)}=\sqrt{tr(A{A}^H)}=\sqrt{\sum |a_{ij}{|}^2}$ 为A的F范数

b. 向量范数定义

设 $V$ 是数域 $F$ (实数域或复数域) 上的线性空间，若对于任一 $X\in V$ ，对应一个非负数，记为 $\Vert X\Vert$ 满足以下三个条件，则称 $\Vert X\Vert$ 为空间 V 上的一个向量范数

• 正性：$\Vert X\Vert >0$
• 齐次性： $\Vert kX\Vert =|k|\Vert X\Vert$
• 三角不等式：$\Vert X+Y\Vert \le \Vert X\Vert +\Vert Y\Vert$

相当于规定在空间V上的一个非负函数 $\phi (x)=\Vert x\Vert ,x\in V$ ，满足正性，齐性，三角性

可知 $C^n$ 上有很多(无穷) 个范数

范数定义2：若线性空间 $V$ 上有一个函数 $\phi (x),x\in V$ 适合

• 正性：$\phi (x)>0,x\ne 0$
• 齐性：$\phi (kx)=|k|\phi (x),x\in V$
• 三角形：$\phi (x+y)\le \phi (x)+\phi (y)$

则称 $\phi (x)$ 为 $V$ 上的一个范数，记为 $\phi (x)=\Vert x\Vert$

eg：

验证给定函数是否为范数

$$\begin{array}{rl}& \because A>0,则由平方根公式A=B^2=B^{H}B\Rightarrow X^{H}AX=X^H{B}^{H}BX=|BX{|}^2\\ & \Rightarrow \Vert x\Vert =\sqrt{|BX{|}^2}=\Vert BX{\Vert }_2>0,且满足齐性\\ & \Vert x+y\Vert =\Vert B(x+y){\Vert }_2=\Vert Bx+By{\Vert }_2\le \Vert Bx{\Vert }_2+\Vert By{\Vert }_2=\Vert x\Vert +\Vert y\Vert ,满足三角性\end{array}$$

---

c. 复向量空间中常用范数

1-范数：$\Vert x{\Vert }_1=\sum (|x_1|+\cdots +|x_n|)$

2-范数：$\Vert x{\Vert }_2=\sqrt{(x,x)}=\sqrt{|x_1{|}^2+\cdots +|x_n{|}^2}$

$\infty$-范数：$\Vert x{\Vert }_{\infty }=max\{|x_1|,\cdots ,|x_n|\}$

p-范数：$\Vert x{\Vert }_p={\left(\sum _{i=1}^n|x_i{|}^2\right)}^{\frac{1}{2}},p\ge 1$

d. 向量范数性质

单位化公式：$X\ne 0$ ，则 $\frac{X}{\Vert X\Vert }$ 是范数为1的向量

$\Vert -X\Vert =\Vert X\Vert$

$\Vert X-Y\Vert \ge |\Vert X\Vert -\Vert Y\Vert |$

e. 有限维线性空间上范数等价性

对于 $C^n$ 上任两个范数 $\Vert X{\Vert }_a$ ，$\Vert X{\Vert }_b$ 存在正数：$k_1>0,k_2>0$ ，使 $k_1\Vert X{\Vert }_b<\Vert X{\Vert }_a<k_2\Vert X{|}_b$ 对一切x成立，即 $k_1\le \frac{\Vert X{\Vert }_a}{\Vert X{\Vert }_b}\le k_2$ ，对一切X成立

证明

f. 范数收敛定理

收敛定义

设 $C^n$ 中向量序列：$X^{(k)}=\left(X_1^{(k)},X_2^{(k)},\cdots ,,X_n^{(k)}\right)$ ($k=1,2,\cdots$) ，$\alpha ={\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_n\right)}^T$ ，若 $X_1^{(k)}\to {\alpha }_1$ ，$X_2^{(k)}\to {\alpha }_2$ ,$\cdots$ ，$X_n^{(k)}\to {\alpha }_n$ （$k\to \infty$），则称 $X^{(k)}\to \alpha$ ，或 $\lim X^{(k)}=\alpha$
$$X^{(k)}\to \alpha ⟺\Vert X^{(k)}-\alpha \Vert \to 0$$

按范数收敛

设 $X_1,\cdots ,X_m,\cdots$ 是线性空间V中的元素序列，若 $X_0\in V$ ，使 $\underset{m\to \infty }{\lim }\Vert X_m-X_0{\Vert }_{\alpha }=0$ ，称序列 $\{X_m\}$ 按范数 $\Vert \bullet {\Vert }_{\alpha }$ 收敛于 $X_0$ ，记为 $\underset{m\to \infty }{\lim }{X}_m\stackrel{\alpha }{}{X}_0$

• 若序列 $\{X_m\}$ 按某一范数收敛于 $X_0$ ，则 $\{X_m\}$ 按任何范数都收敛于 $X_0$ ，即有限维空间按范数收敛是互相等价的

  

• 序列 $\{X_m\}$ 按范数收敛于 $X_0$ $⟺$ 按坐标收敛于 $X_0$
  取一组基底 e 1 , e 2 , ⋯   , e n ，令 X m = ξ 1 ( m ) e 1 + ⋯ + ξ n ( m ) e n , X 0 = ξ 1 ( 0 ) e 1 + ⋯ + ξ n ( 0 ) e n 由二范数定义 , ∀ x = ( ξ 1 ξ 2 ⋮ ξ n ) ∈ C n , ∥ X ∥ 2 = ( ∑ i = 1 n ∣ ξ i ∣ 2 ) 1 2 按范数收敛是等价的， ∴ lim ⁡ m → ∞ ∥ X m − X 0 ∥ = 0    ⟺    lim ⁡ m → ∞ ∥ X m − X 0 ∥ 2 = 0    ⟺    lim ⁡ m → ∞ ( ∑ i = 1 n ∣ ξ i ( m ) − ξ i ( 0 ) ∣ 2 )    ⟺    lim ⁡ m → ∞ ξ i ( m ) = ξ i ( 0 ) \begin{aligned} &取一组基底e_1,e_2,\cdots,e_n，令X_m=\xi_1^{(m)}e_1+\cdots+\xi_n^{(m)}e_n,X_0=\xi_1^{(0)}e_1+\cdots+\xi_n^{(0)}e_n\\ &由二范数定义,\forall x=\left( \begin{matrix} \xi_1\\\xi_2\\\vdots\\\xi_n \end{matrix} \right)\in C^n,\Vert X\Vert_2=(\sum_{i=1}\limits^n\vert \xi_i\vert^2)^{\frac{1}{2}}\\ &按范数收敛是等价的，\therefore\lim_{m\rightarrow \infty}\Vert X_m-X_0\Vert=0\iff \lim_{m\rightarrow \infty}\Vert X_m-X_0\Vert_2=0\\ &\iff \lim_{m\rightarrow \infty}(\sum_{i=1}\limits^n\vert \xi_i^{(m)}-\xi_i^{(0)}\vert^2 )\iff \lim_{m\rightarrow \infty}\xi_i^{(m)}=\xi_i^{(0)} \end{aligned} ​取一组基底e1​,e2​,⋯,en​，令Xm​=ξ1(m)​e1​+⋯+ξn(m)​en​,X0​=ξ1(0)​e1​+⋯+ξn(0)​en​由二范数定义,∀x= ​ξ1​ξ2​⋮ξn​​ ​∈Cn,∥X∥2​=(i=1∑n​∣ξi​∣2)21​按范数收敛是等价的，∴m→∞lim​∥Xm​−X0​∥=0⟺m→∞lim​∥Xm​−X0​∥2​=0⟺m→∞lim​(i=1∑n​∣ξi(m)​−ξi(0)​∣2)⟺m→∞lim​ξi(m)​=ξi(0)​​

6.1.2 矩阵范数

a. 矩阵范数定义

对于一个方阵 $A\in C^{n,n}$ ，矩阵范数 $\Vert A\Vert$ 表示某个法则与A对应的非负函数，且满足4个条件：

• 正性：$A\ne 0$ 时，$\Vert A\Vert >0$ ，当且仅当 $A=0$ 时， $\Vert A\Vert =0$
• 齐性：$\Vert kA\Vert =|k|\cdot \Vert A\Vert ,\forall k\in C$
• 三角形：对于任两个矩阵 $A,B\in C^{n,n}$ ，有 $\Vert A+B\Vert \le \Vert A\Vert +\Vert B\Vert$
• 相容性（次乘性）：$\Vert AB\Vert \le \Vert A\Vert \cdot \Vert B\Vert ,A,B\in C^{n,n}$

则 $\Vert A\Vert$ 为矩阵范数（相容范数）

---

矩阵范数定义2：设方阵空间 $C^{n\times n}$ 上非负函数 $\phi (A),A\in C^{n\times n}$ ，有：

• 正性：$\phi (A)>0(A\ne 0)$
• 齐性：$\phi (kA)=|k|\phi (A),k\in C$
• 三角形：$\phi (A+B)\le \phi (A)+\phi (B),A,B\in C^{n\times n}$
• 相容性：$\phi (AB)\le \phi (A)\cdot \phi (B)$

则称 $\phi (A)$ 为空间 $C^{n\times n}$ 上的矩阵范数，记为 $\phi (A)=\Vert A\Vert$

b. 常用范数

令方阵 $A=(a_{ij}{)}_{n\times n}\in C^{n\times n}$

• 1-范数(最大列和)：$\Vert A{\Vert }_1=\underset{j}{\max }\sum _{i=1}^n|a_{ij}|,j=1,\cdots ,n$

  列是一个数据，对应的是向量范数的1-范数，能代表一个列向量

• $\infty$ 范数(最大行和)：$\Vert A{\Vert }_{\infty }=\underset{i}{\max }\sum _{j=1}^n|a_{ij}|(i=1,\cdots ,n)$

  行是一个维度，对应的是向量范数的 $\infty$ -范数，能代表一个维度特征

• 2-范数(谱范数)：$\Vert A{\Vert }_2=({\lambda }_1(A^{H}A){)}^{\frac{1}{2}}$ ，${\lambda }_1(A^{H}A)$ 表示 $A^{H}A$ 的最大特征值，即 $\Vert A{\Vert }_2$ 是 A 的最大特征值

• 总和范数：$\Vert A{\Vert }_M=\sum |a_{ij}|$

• F-范数：$\Vert A{\Vert }_F=(\sum |a_{ij}{|}^2{)}^{\frac{1}{2}}=\sqrt{tr(A^{H}A)}$

• G-范数：$\Vert A{\Vert }_G=n\cdot max\{|a_{ij}|\}$

eg

---

几种范数关系

$$\begin{array}{rl}& \Vert A{\Vert }_{\infty }=\Vert A^H{\Vert }_1,\Vert A{\Vert }_1=\Vert A^H{\Vert }_{\infty }\\ & \Vert A{\Vert }_2=\Vert A^H{\Vert }_2,\Vert A{\Vert }_F=\Vert A^H{\Vert }_F=(tr(A^{H}A){)}^{\frac{1}{2}}\\ & U,V为U阵，则\Vert UA{\Vert }_F=\Vert AV{\Vert }_F=\Vert UAV{\Vert }_F=\Vert A{\Vert }_F\\ & A\in C^{n\times n}，x\in C^n,则\Vert Ax{\Vert }_2\le \Vert A{\Vert }_F\Vert x{\Vert }_2\end{array}$$

c. 矩阵范数性质

1. $\Vert A\pm B\Vert \le \Vert A\Vert +\Vert B\Vert$

   

2. $\Vert AB\Vert \le \Vert A\Vert \cdot \Vert B\Vert$

   

3. 幂公式：$\Vert A^k\Vert \le \Vert A{\Vert }^k$

   $\Vert I\Vert \ge 1$

   谱半径幂公式：$\rho (A^k)\le [\rho (A){]}^k$ ，k=1,2,…
   $$\begin{array}{rl}& 由谱半径定义\rho (A)=max\{|{\lambda }_1|,|{\lambda }_2|,\cdots ,|{\lambda }_n|\}，\\ & 其中方阵A=A_{n\times n}特征值\lambda (A)=\{{\lambda }_1,\cdots ,{\lambda }_n\}\\ & 可知\lambda (A^k)=\{{\lambda }_1^k,\cdots ,{\lambda }_n^k\}\Rightarrow \rho (A^k)=max\{|{\lambda }_1{|}^k,\cdots ,|{\lambda }_n{|}^k\}=[\rho (A){]}^k\end{array}$$

4. 公式：$\Vert kA\Vert =|k|\cdot \Vert A\Vert$ ，$\rho (kA)=|k|\rho (A)$

   SP：$\Vert -A\Vert =\Vert A\Vert$ ，$\rho (-A)=\rho (A)$

d. 矩阵范数定理

1. $A\in C^{m\times n}$ 的任一范数都是A的元素的连续函数
2. 任两个范数等价，即对2个范数 $\Vert A{\Vert }_{\alpha }.\Vert A{\Vert }_{\beta }$ ，存在正数 $k_1,k_2$ ，使得 $\forall A\in C^{m\times n}$ ，都有 $k_1\Vert A{\Vert }_{\beta }\le \Vert A{\Vert }_{\alpha }\le k_2\Vert A{\Vert }_{\beta }$ ，即$k_1\le \frac{\Vert A{\Vert }_{\alpha }}{\Vert A{\Vert }_{\beta }}\le k_2$
3. 矩阵序列 $A_k$ 按任一范数收敛于 $A_0⟺$ 按元素收敛 $\underset{k\to \infty }{\lim }{a}_{ij}^k=a_{ij}^0,\forall i,j$

SP ： 任一矩阵范数 $\Vert A\Vert$ 都和总和范数 $\Vert A{\Vert }_M=\sum |a_{i,j}|$ 等价，存在整数 $k_1$,$k_2$ ，使 $k_1\le \frac{\Vert A\Vert }{\Vert A{\Vert }_M}\le k_2$

$\frac{1}{n}\le \frac{\Vert A{\Vert }_1}{\Vert A{\Vert }_M}\le 1$ ，$\frac{1}{n}\le \frac{\Vert A{\Vert }_{\infty }}{\Vert A{\Vert }_M}\le 1$ ，$\frac{1}{n}\le \frac{\Vert A{\Vert }_F}{\Vert A{\Vert }_M}\le 1$