NEUQ-acm第二次双周赛补题

7-1 输出全排列

题目描述

请编写程序输出前n个正整数的全排列（n<10），并通过9个测试用例（即n从1到9）观察n逐步增大时程序的运行时间。

输入格式

输入给出正整数n（<10）。

输出格式

输出1到n的全排列。每种排列占一行，数字间无空格。排列的输出顺序为字典序，即序列$a_1,a_2,\cdots ,a_n$ 排在序列$b_1,b{}_2,\cdots ,b_n$​之前，如果存在$k$使得$a_1=b_1,\cdots ,a_k=b_k$并且$a_k+1<b_k+1$ 。

输入样例

3

输出样例

123
132
213
231
312
321

思路

全排列问题，dfs深搜+回溯

代码1

#include 
using namespace std;
const int Max=15;
int vis[Max];
int a[Max];
int n;
void print(){
    for(int i=1; i<= n; i++){
        cout << a[i];
    }
    cout << endl;
}
void dfs(int x){
    for(int i = 1; i <= n; i++){
        if(vis[i]==0){
            a[x]=i;
            vis[i]=1;
            dfs(x+1);
            vis[i]=0;
        }
    }
    if(x==n){
        print();
        return;
    }
}
int main(){
    cin >> n;
    dfs(1);
}

代码2

新发现了一个$next$_$permulation$() 函数，更简单

#include 
using namespace std;
const int Max=15;
char a[Max];
int n;
int main(){
    cin >> n;
    for(int i = 0; i < n; i++){
        a[i]='0'+i+1;
    }
    do{
        for(int i = 0; i < n; i++){
            cout << a[i];
        }
        cout << endl;
    }while(next_permutation(a,a+n));
}

7-2 山

题目描述

Drizzle 前往山地统计大山的数目，现在收到这片区域的地图，地图中用0（平地）和1（山峰）绘制而成，请你帮忙计算其中的大山数目
山总是被平地四面包围着，每一座山只能在水平或垂直方向上连接相邻的山峰而形成。一座山峰四面被平地包围，这个山峰也算一个大山
另外，你可以假设地图的四面都被平地包围着。

输入格式

第一行输入M,N分别表示地图的行列，接下来M行每行输入N个数字表示地图

输出格式

输出一个整数表示大山的数目

输入样例

4 5
1 1 0 0 0
1 1 0 0 0
0 0 1 0 0
0 0 0 1 1

输出样例

3

数据范围

对于 5% 的数据：M，N ≤ 10
对于 100% 的数据：M，N ≤ 2000

思路

求有几个连通图和孤点数总和，遍历一遍图，用了几次队列

代码

#include 
using namespace std;
const int Max=2*1e3+5;
int n,m;
int mapp[Max][Max];
int vis[Max][Max];
int next_x[4]={-1, 0, 1, 0};
int next_y[4]={0, 1, 0, -1};
queue< pair<int, int> > q;
int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            int s;
            cin >> s;
            mapp[i][j]=s;
        }
    }
    int ans=0;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j<= m; j++){
            if(vis[i][j]==1 || mapp[i][j]==0) continue;
            vis[i][j]=1;
            q.push(make_pair(i,j));
            while(!q.empty()){
                int nx=q.front().first;
                int ny=q.front().second;
                q.pop();
                for(int i=0; i < 4; i++){
                    int nextx=nx+next_x[i];
                    int nexty=ny+next_y[i];
                    if(vis[nextx][nexty]==0 && nextx>0 && nextx<=n && nexty>0 && nexty<=m && mapp[nextx][nexty]==1){
                        q.push(make_pair(nextx,nexty));
                        vis[nextx][nexty]=1;
                    }
                }
            }
            ans++;
        }
    }
    cout << ans;
}

7-3 跳跃

题目描述

Drizzle 被困到一条充满数字的方块路中，假设这条路由一个非负的整数数组m组成，Drizzle 最开始的位置在下标 start 处，当他位于下标i位置时可以向前或者向后跳跃m[i]步数，已知元素值为0处的位置是出口，且只能通过出口出去，不可能数组越界，请你通过编程计算出Drizzle能否逃出这里。

输入格式

第一行输入数组m的长度n 第二行输入数组元素，空格分割开 第三行输入起始下标start

输出格式

可以出去，输出True ，否则输出False。

输入样例

7
4 2 3 0 3 1 2
5

输出样例

True

数据范围

1 <= m.length <= 5 * 10^4
0 <= m[i] < m.length
0 <= start < m.length

思路

dfs深搜
如果下一个值为出口，则标记答案，可以搜到
否则，深搜下一个next=now±m[now]
注意范围

代码

#include 
using namespace std;
const int Max=5*1e4+5;
int n;
int m[Max];
int start;
int ans=0x3ffffff;
int vis[Max];
void dfs(int now){
    if(m[now]==0 && now>=0 && now<n) ans=1;  //到出口了
    if(vis[now]==0 && now>=0 && now<n && m[now]!=0){
        vis[now]=1;
        if(now+m[now] < n && vis[now+m[now]]==0) dfs(now+m[now]);
        if(now-m[now] >= 0 && vis[now-m[now]]==0) dfs(now-m[now]);
        vis[now]=0;
    }
}
int main(){
    cin >> n;
    for(int i = 0; i < n; i++){
        cin >> m[i];
    }
    
    cin >> start;
    dfs(start);
    //cout << ans;
    if(ans!=0x3ffffff)  cout << "True";
    else cout << "False";
}

7-4 回文数文回

题目描述

我们称一个数是回文的，当且仅当它正着读和倒着读是相同的。

例如11或11455411是回文的，而10或1919810不是回文的。

现在给定一个数n，你需要求出区间$[10^8,n]$中所有的回文数。

输入格式

一行一个整数$n(10^8\le n<10^9)$

输出格式

输出一行一个数，表示题目所求区间中回文数的数量。

输入样例

100000001

输出样例

1

思路

在范围内，回文数的个数最多只有$9\ast 10\ast 10\ast 10\ast 10$个数，所以我们直接构造回文数，以中间的数平分，中间有10种可能，两边采用dfs构造回文数，注意最外边只有9种可能（不能取0），递归结束条件：已经构造了四次。

代码

#include 
using namespace std;
int n;
int a[9];
int ans;
bool Isrange(){
    int x=0;
    for(int i = 0; i < 9; i++){
        x+=a[i]*pow(10,i);
    }
    if(x >= 1e8 && x <= n)  return true;
    else  return false;
}

void dfs(int s){
    if(s==5){
        if(Isrange()) ans++;
        return;
    }
    if(s==4){
        for(int i=1; i <= 9; i++){
            a[4-s]=i;
            a[4+s]=i;
            dfs(s+1);
        }
    }
    else{
        for(int i = 0; i <= 9; i++){
            a[4-s]=i;
            a[4+s]=i;
            dfs(s+1);
        }
    }
}
int main(){
    cin >> n;
    for(int i = 0; i <= 9; i++){
        a[4]=i;
        dfs(1);
    }
    cout << ans << endl;
}

7-5 最长光路

题目描述

小明在做丁达尔效应的实验。
他用胶体填满了一个有 N 行, M 列个格子的透明盒子。同时，为了使实验效果更好，他在盒子的某些格子中装入一些双面镜(用“/”和“\”表示)。
当光线找到双面镜的时候，光路会反射，方向会有90度的转换（如下图所示）。

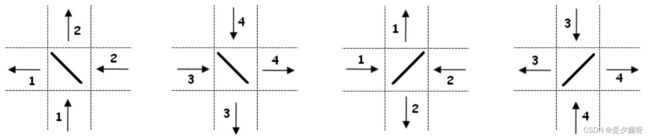
小明在填充胶体的时候产生了失误，使得有些格子光线无法穿过（我们可以认为这些格子把光线都吸收了），这些格子用大写字母“C”来表示。

现在，小明已经制作好了实验装置，他将激光光源放在第sx行的第sy个格子上。激光光源可以朝向上下左右四个方向，分别用URDL四个字母表示(“U”-上, “R”-右, “D”-下, “L”-左)。

为了让实验效果更好，小明希望光的光路越酷越好。
对小明来说，最酷的光路就是包含环的光路，这种情况下，光不会射向盒子外面，而是一直在盒子内循环（数据保证光源处的点是光线可以通过，即起点一点是"."）。
如果光源朝各个方向摆设，最终光线都会射向盒子外部，那么小明认为经过格子最多的光路是最酷的。

现在小明想知道光源朝哪个方向放置光路最酷。
如果光路是不包含环的，那么他还想知道光路经过的格子数目是多少。

注意
如果有多个方向是最优解，那么我们按照“U”-上, “R”-右, “D”-下, “L”-左的优先级来选择最终的答案，即如果向左和向右都是最优解，我们选择向右的方案。

同时，温馨提醒，c++中“\”符号可以用’\'来表示

输入格式

第一行两个数 N,M(1≤N,M≤500) 表示有N 行 M 列的格子。
接下来 N 行, 每行 M 个字符，表示盒子的具体情况。 “/”和“\”表示装有不同朝向的镜子的格子。“C”表示光线无法通过的格子。“.”表示正常且没有镜子的格子。
最后输入两个数字sx,sy表示光源所在的点。

输出格式

第一行输出一个大写字母，表示最酷的光路应该超哪个方向摆放。
第二行输出光路经过的格子数。如果光路中包含环，则换成输出字符串“COOL”。

输入样例1

5 5
../.\
.....
.C...
...C.
\.../
3 3

输出样例1

U
17

输入样例2

5 7
/.....\
../..\.
\...../
/.....\
\.\.../
3 3

输出样例

R
COOL

样例解释

S为起点
../.\
.....
.CS..
...C.
\.../

'U' 方向
*.***
*.*.*
*C*.*
*..C*
*****
17个格子


'R'方向
../.\
.....
.C***
...C.
\.../
3个格子


'D'方向
../.\
.....
.C*..
..*C.
\.*./
3个格子

'L'方向
../.\
.....
.C*..
...C.
\.../
1个格子

思路

对每个点的不同方向是否访问过进行存储，所以就要用到三维数组
接下来进行dfs搜索，如果某个点的同一方向走过两次，那么就是有环。
注意：下一个坐标要与光的朝向相对应，另外要求优先的光向顺序：上右下左

代码

#include 
using namespace std;
const int Max=0x3ffffff;
int N,M;  //N行M列格子
char c;
int ans, len;
int sx, sy;  //光源坐标
char mapp[505][505];
bool vis[505][505][4];  //带方向的图
int nextx[4]={-1, 0, 1, 0};
int nexty[4]={0, 1, 0, -1};
char fangx[4]={'U', 'R', 'D', 'L'};  //朝向
bool Istong(int x, int y){
    return x>=1 && y>=1 && x<=N && y<=M && mapp[x][y]!='C';
}
void dfs(int x, int y, int f){
    len++;
    if(vis[x][y][f]){
        len= Max;
        return;
    }
    else  vis[x][y][f]=1;
    if(mapp[x][y]=='\\'){
        if(fangx[f]=='U') f=3;
        else if(fangx[f]=='R') f=2;
        else if(fangx[f]=='D') f=1;
        else  f=0;
    }
    if(mapp[x][y]=='/'){
        if(fangx[f]=='U') f=1;
        else if(fangx[f]=='R') f=0;
        else if(fangx[f]=='D') f=3;
        else f=2;

    }
    if(Istong(x+nextx[f], y+nexty[f])){
        dfs(x+nextx[f], y+nexty[f], f);
    }
    else return;

}
int main(){
    cin >> N >> M;
    for(int i = 1; i <= N; i++){
        for(int j = 1; j <= M; j++){
            cin >> mapp[i][j];
        }
    }
    cin >> sx >> sy;
    for(int i = 0; i < 4; i++){
        memset(vis, 0, sizeof(vis));
        len=0;
        dfs(sx,sy,i);
        if(len > ans){
            ans=len;
            c=fangx[i];
        }
    }
    cout << c << endl;
    if(ans < Max) cout << ans;
    else  cout << "COOL" << endl;
}