目标追踪-meanshift算法
目标追踪-meanshift算法
原理简介
- 开始
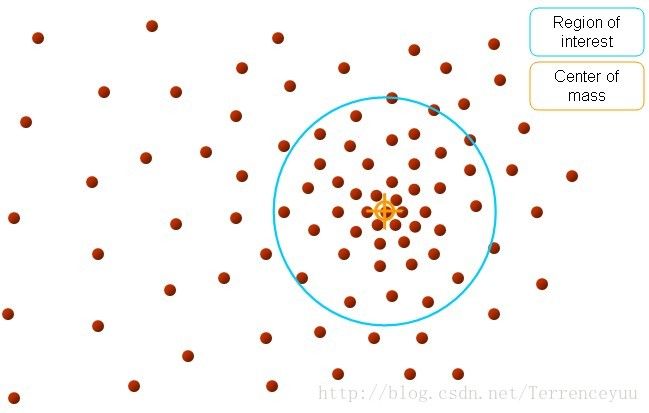
如上图所示,meanshift算法原理概括如下:
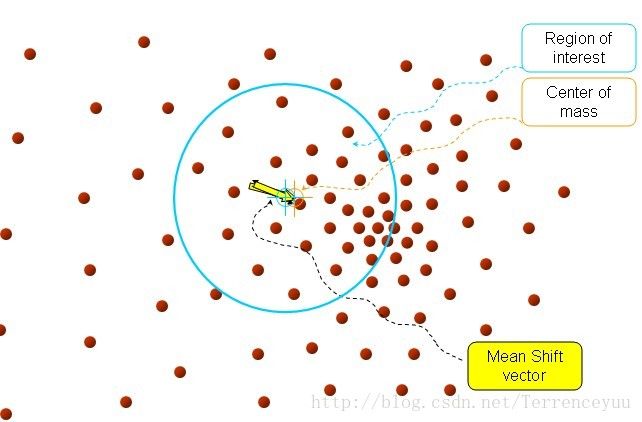
首先设定起始点x,就是圆的圆心。 所有在球内的点就是xi , 黑色箭头就是我们计算出来的向量xxi , 将所有的向量 xxi进行求和计算平均就得到我们的meanshift 向量,也就是图中黄色的向量。
接着,再以meanshift向量的终点为圆心,再做一个高维的球,如下图所示,重复上面的步骤,最终就可以收敛到点的分布中密度最大的地方
算法的推到可参见博客:
http://www.cnblogs.com/liqizhou/archive/2012/05/12/2497220.html
算法实现
# coding:utf-8
# 设置感兴趣区域的彩色直方图 - 反投影到一副图像上 - 作为meanshift算法参数(prob image)输入得到新的追踪区域
import numpy as np
import cv2
from MyCvUtils import MyCvUtils
datapath = "D:/imgData/"
cap = cv2.VideoCapture(0)
# capture the first frame
ret,frame = cap.read()
# mark the ROI
r,h,c,w = 10, 200, 10, 200
track_window = (c,r,w,h)
# extract the ROI for tracking
roi = frame[r:r+h, c:c+w]
# switch to HSV
hsv_roi = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
# create a mask with upper and lower boundaries of colors you want to track
# 指定感兴趣的颜色
mask = cv2.inRange(hsv_roi, np.array((10., 30.,32.)), np.array((20.,120.,255.)))
# calculate histograms of roi
# p2:通道 p4:每个维度下直方图数组的大小 p5每个维度下直方图的上下界
roi_hist = cv2.calcHist([hsv_roi],[0],mask,[180],[0,180])
# 将直方图的值归一化0-255
cv2.normalize(roi_hist,roi_hist,0,255,cv2.NORM_MINMAX)
# MyCvUtils.saveArr(roi_hist, datapath+'roi_hist')
# Setup the termination criteria, either 10 iteration or move by atleast 1 pt
# 得到终止条件:均值漂移迭代10次或中心移移动至少一个像素,均值漂移就停止计算中心移动
term_crit = ( cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 10, 1 )
while(1):
ret ,frame = cap.read()
if ret == True:
hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV)
# 执行直方图反向投影, 每个像素以概率的形式表示
dst = cv2.calcBackProject([hsv],[0],roi_hist,[0,180],1)
# MyCvUtils.saveArr(dst, datapath+'dst')
# apply meanshift to get the new location
ret, track_window = cv2.meanShift(dst, track_window, term_crit)
# Draw it on image
x,y,w,h = track_window
img2 = cv2.rectangle(frame, (x,y), (x+w,y+h), 255,2)
cv2.imshow('img2',img2)
k = cv2.waitKey(60) & 0xff
if k == 27:
break
else:
break
cv2.destroyAllWindows()
cap.release()