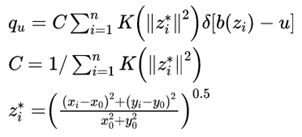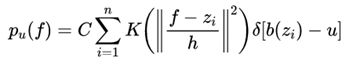meanshift跟踪算法
以下是用meanshift实现目标跟踪的实验报告（包含源码），实验中详细介绍了meanshift跟踪算法的原理，结合OTB100跟踪数据集对meanshift跟踪效果进行了分析。
目 录
一.实验名称
二.实验目的
三.实验原理
3.1 前言
3.2 meanshift
四.实验测试
4.1 测试条件
4.2 性能分析
五.实验总结
一.实验名称
使用meanshift实现目标跟踪。
二.实验目的
根据meanshift原理实现目标跟踪，达到跟踪指定目标的效果。
三.实验原理
3.1 前言
目标追踪作为计算机视觉中的一个重要的方面，它的主要的研究挑战来自于刚性与非刚性的形变，目标被部分或者完全遮挡，目标突然消失，目标剧烈运动，复杂的背景变换，特别是出现目标与背景及其相似的时候等，以上这些影响因素都会对目标追踪算法的效果造成很大的影响。针对这些挑战，不同性能优秀的跟踪算法应运而生，也在各个应用方面取得了不错的效果。
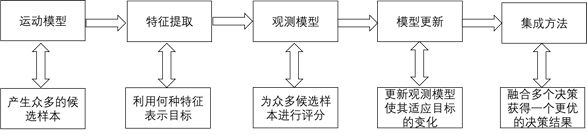
目标跟踪的流程可以大致分为五个部分的内容，如下图3.1所示。
图3.1 目标跟踪算法通用流程图
目标跟踪会先根据初始框选取若干候选框作为候选样本，接着利用这些初始框与候选框提取出相应的特征，进而对这些特征进行对比，找出候选样本中与目标样本特征最相似的一个即为新的目标。最后用新的目标特征进行模型更新，以此类推，逐步跟踪目标。
目标跟踪虽然已经发展起来，并且有了大致的研究流程，但是大部分还是停留在理论阶段，许多跟踪算法无法落地到工业应用，所以需要进一步的投入更多的研究，特别是在既保证准确率的基础上又可以满足各种场景的实时性跟踪目前仍然是一件不容易的事情。
本文是基于目标跟踪算法meanshift的研究，详细分析meanshift跟踪算法的原理以及效果，其适合的跟踪场景等等。
3.2 meanshift
3.2.1 简介
Meanshift算法属于无参数核密度估计法，即该算法本身不需要任何的先验知识而完全依靠特征空间中的样本点，进而计算密度函数。在空间进行采样，在采样充分的情况下，其能够渐进的收敛于任意的密度函数，即可以服从任意数据的密度估计。
给定的d维空间
中的n个样本点
,i=1,…n,在x点mean shift向量的基本定义形式为：
(1)
其中
是在一个半径为h的高维球区域，满足以下关系的y点的集合，
(2)
k表示在这n个样本点
中有k个点落入到
区域中。
从公式中可以看出(xi-x) 是样本点
相对于x的偏移量，公式（1）相当于就是定义的落入
中的样本点相当于x的偏移量求和之后的平均值。
区域中更多的样本点肯定是落在梯度密度的方向，所以meanshift向量
会指向概率密度梯度的方向。
3.2.1 跟踪算法原理
基于均值漂移的meanshift跟踪算法可以通过分别计算目标区域与下一帧中的目标候选区域内的像素特征概率得到上一帧的目标模型与当前帧的候选模型。利用相似性度量函数比较目标模型与候选模型之间的相似性，选择相似性最大的候选模型并得到关于目标模型的meanshift向量，目标从上一帧的位置沿着该meanshift向量进行移动，通过不断的迭代，算法最终可以收敛到目标的位置，达到跟踪的目的。
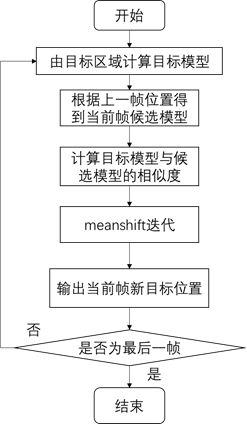
Meanshift跟踪算法的流程图如下图3.2所示。
图3.2 meanshift跟踪算法原理图
（1）通过手工选取等方式在第一帧中选取目标区域，目标中心坐标为(x0,y0),计算目标模型的概率密度
。
(3)
其中n个像素用
表示目标模型的位置，对选中的区域的颜色空间进行均匀划分，得到有m个相等的区间构成的灰度直方图。目标模型的
就可以用上面的公式描述。
表示以目标中心为原点的归一化像素位置，(x0,y0)表示目标中心的坐标，K为核函数，这里之所以引入核函数是因为从公式（1）可以看出，在
区域中的点对于meanshift偏移向量的贡献都是一样的，然而实际中我们希望离目标中心距离越近的点对于该向量的贡献越大，越远侧贡献越小，为此我们引入核函数，在本文中，我们采用Epannechnikov核函数：
(4)
该核函数满足三个性质：非负性，非递增性，分段连续。
表示在
处的像素处于哪个直返图区间，u为直方图的颜色索引。
函数的作用是判断目标区域中像素
处的像素值是否属于直方图的第u个单元，属于的话为1，否则为0，C为归一化系数。
（2）跟踪上一帧的中心坐标初始化当前帧的目标位置，计算候选目标的模型
在当前帧中，根据上一帧的目标中心位置
作为搜索中心，得到候选目标的中心位置坐标
,计算当前帧的候选目标区域直方图。该区域的像素用
表示，该候选模型的概率密度函数为：
(5)
其中h为核函数窗口的大小，决定着权重分布。
（3）计算目标模型与当前帧候选模型的相似度。
本文采用Bhattacharyya系数作为相似性函数，定义为：
(6)
相似性函数值越大表示两个模型越相似，将前一帧中目标的中心位置作为当前帧搜索中心，寻找相似度最大的候选区域就是当前帧中目标的位置，
（4）meanshift迭代过程
Meanshift的迭代过程就是从上一帧的目标位置向当前帧的目标位置移动的过程，为了让相似性函数最大，对上式进行泰勒展开，得到Bhattacharyya系数的近似表达：
(7)
其中以上公式的值只随着
的变化而变化，其极大值的过程就是通过候选区域向真实区域中心meanshift迭代完成：
(8)
其中
,meanshift方法就是从
起向两个模型相比颜色变化最大的方向不断移动，直到两次移动距离小于阈值，即找到当前帧中的目标位置，依次作为下一帧的起始目标搜索位置，不断重复得到后续帧中的目标位置。
四.实验测试
4.1 测试条件
4.1.1 测试环境
（1）硬件环境：windows10的操作系统；CPU: intel(R) Core(TM) i5-5200U CPU @2.2GHZ；RAM:8GB。
（2）软件环境：算法用python在pycharm中实现。
4.1.2 评估指标
目标跟踪算法的评估方法通常可以分为定量分析与定性分析两种。定性分析就是直接将跟踪的结果显示在视频序列中，这个时候可以直接通过人眼来观察，进而判断跟踪算法的好坏，是一个比较主观的方式。相对于定性分析，定量分析显得客观的多，本实验采用一般的定量评估方法包括精度与IOU值。
精度（precision）表示的是跟踪算法估计的目标位置的中心与人工标注的目标的中心点，这两点之间的距离值，这里的距离计算一般取欧式距离。如果是对一段视频序列求精度则是视频序列中的每一帧的精度的平均值。精度的评估方式缺点就是无法反映目标物体大小与尺度的变换情况。
给定人工标准的目标物体ground-truth的box为B，跟踪算法得到的目标物体的bounding box为A。重合率（overlap score，OS）可以定义为：
(9)
其中|.| 表示该区域内的像素数目，本实验的IOU指的就是公式(9)计算的OS
4.1.3 标准数据集
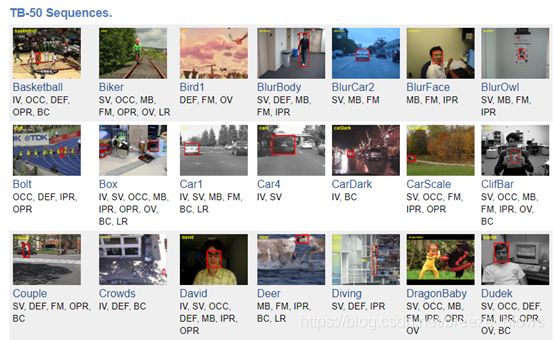
本文采用的测试集来自于在2013年CVPR中提出的视频跟踪基准库(Visual Tracker Benchmark)。该Visual Tracker Benchmark视频库中的TB-50包含了50个视频，其中视频的每一帧都人工标注了ground-truth。该视频库的每一段视频都有各个属性，比如光照变化，运动模糊，遮挡等属性，一共有十一个属性如表4-1所示。这些属性都考验着跟踪算法的性能。使用该数据库可以从各个特性方面有效的评估跟踪算法的性能。TB-50的部分视频信息如下图4.1所示。每一个视频片段包含视频名，该视频序列包含的属性。
图4.1 TB-50部分视频信息图。
表4-1 TB50中各个视频包含的属性解释图
4.2 性能分析
4.2.1 定量分析
本实验对OTB100中所有视频序列进行了测试，按照测试结果与视频属性选取了六个视频序列进行详细的分析，这六个视频序列分别是BlurBody,DragonBaby,Walking2,Bird1,Crowds,skating1。如表4-2所示。
表4-2 实验结果表
其中Dis_center是取每一帧meanshift检测出来的bbox与groundtruth的中心点坐标的欧式距离的平均值。IOU是每一帧meanshift检测出来的bbox与groundtruth的IOU的平均值。
从表中可以很明显的看出meanshift对于前三种视频序列的跟踪效果较好，而对于后面三种视频序列，效果就显得特别的差。对每个视频序列的属性进行分析，发现meanshift对于轻微的形变，运动模糊，旋转，边缘性遮挡等都是鲁棒的，这个从meanshift在前三个视频序列表现好可以看出来。但是meanshift对于目标尺度发现剧烈变化，光线剧烈变化，快速运动，发现严重遮挡都是不鲁棒的，一旦上述情况发现，meanshift都会跟丢目标。
为了更加直观的定量分析meanshift跟踪算法，实验中绘制了BlurBody,DragonBaby,Walking2,Bird1,Crowds,skating1的每一帧中meanshift检测出来的bbox与groundtruth的中心点坐标欧式距离与IOU值的图。
如下图4.2所示，画图按照BlurBody,DragonBaby,Walking2一组，Bird1,Crowds,skating1一组。
(a) (b)
(c) (d)
图4.2 中心点距离与IOU值趋势图
在图4.2中，图(a),(b)对应的是BlurBody,DragonBaby,Walking2，横坐标是帧的序列，纵坐标分别是每一帧中meanshift检测出来的bbox与groundtruth的中心点坐标欧式距离与IOU值。从图中其实可以看出曲线都是很震荡的，这说明了meanshift算法对于视频序列中的属性变换比较敏感，稍微的变化就会引起meanshift的算法性能下降。在图(a)(b)中中心点距离上升与iou下降的原因主要是在视频序列中出现了快速运动与严重遮挡的情况。曲线表现的比较好的帧是因为视频序列中出现了模糊，轻微形变，边缘性遮挡，旋转。所以meanshift还可以较好的跟踪到目标。
图(c),(d)对应的是Bird1,Crowds,skating1，横坐标是帧的序列，纵坐标分别是每一帧中meanshift检测出来的bbox与groundtruth的中心点坐标欧式距离与IOU值。从图(c)(d)中可以看出meanshift之所以效果这么差是因为在视频的前几帧meanshift就出现了跟丢目标的情况，然后就再也找不到正确的目标了，以至于IOU一直稳定在0，出现跟丢是因为目标出现了剧烈运动，光线出现距离变化，出现了很多与目标相似的目标等。
4.2.2 定性分析
为了更加直观的显示meanshift的跟踪效果，以下我们选取了BlurBody，Walking2，Skating1跟踪情况进行分析。
图4.3 BlurBody跟踪效果图
在图4.3中红色框表示groundtruth，绿色框表示meanshift跟踪出来的框，图片左上角表示当前第多少帧。从图中可以看出，当在第1帧与第16帧的时候，目标发生轻微的模糊与形变，meanshift都是可以较好的跟踪到目标的，但是在第189帧与第333帧，目标发现较大的形变以及模糊的时候就跟踪不到了。
图4.4 Walking2跟踪效果图
从图4.4中可以看出在第1帧与第148的时候，目标仅仅是发生了轻微的形变，meanshift跟踪算法可以适应这个改变，但是当在第200帧的时候，出现了想与目标相似的人而且发现了严重遮挡，直接导致在第268帧的时候已经完全跟丢了目标。
图4.5 Skating1跟踪效果图
从图4.5中可以看出，当在第1帧与第57帧的时候，目标发现缓慢的移动，meanshift跟踪算法可以较好的适应这种变化，但是当在第85帧的时候，目标发现快速移动，meanshift跟踪算法就直接跟丢了目标，导致在后续的帧比如第132帧的目标一直处于被跟丢的状态。
五.实验总结
Meanshift跟踪算法的主要原理就是建模前后两帧的目标模型与候选帧模型，对比目标模型与候选帧模型之间的相似性，最后进行meanshift迭代找到当前帧中最可能的目标位置。
本次实验按照meanshift的原理实现了meanshift跟踪算法，并且利用meanshift跟踪算法在OTB100数据集上面进行了测试，最后对测试结果进行了详细分析。实验发现meanshift跟踪算法对于轻微的形变，模糊，边缘遮挡，旋转具有较好的鲁棒性，但是当目标出剧烈形变，快速移动，严重遮挡，光线距离变化等情况时，meanshift的跟踪算法就会显得特别差。
Meanshift的主要不足就是难以适应目标的尺度变化，没有尺度更新机制，没有模型更新机制，难以适应目标的实时变化，主要提取的颜色直方图特征，该特征不够鲁棒，难以适应目标的负责变化。这些难点都是以后需要去研究的方向。
源代码：
import numpy as np
import cv2
import os
import re
import math
import matplotlib.pyplot as plt
def axis_aligned_iou(boxA, boxB):
assert(boxA[0] <= boxA[2])
assert(boxA[1] <= boxA[3])
assert(boxB[0] <= boxB[2])
assert(boxB[1] <= boxB[3])
xA = max(boxA[0], boxB[0])
yA = max(boxA[1], boxB[1])
xB = min(boxA[2], boxB[2])
yB = min(boxA[3], boxB[3])
interArea = max(0, xB - xA + 1) * max(0, yB - yA + 1)
boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
iou = interArea / float(boxAArea + boxBArea - interArea)
return iou
def center_dis(centerA, centerB):
return math.sqrt(sum(pow(np.array(centerA)-np.array(centerB), 2.0)))
result = open('result.txt', 'a')
root_path = '/home/hello/dataset/OTB50/'
tb50 = ['BlurBody','BlurFace','DragonBaby','Walking2','Walking','Surfer']
# tb50 = ['BlurBody','DragonBaby','Walking2']
# tb50 = ['Bird1','Crowds','Skating1']
# tb50 = ['BlurBody','Walking2','Skating1']
for dataset in tb50:
result_path = 'result/{}/'.format(dataset)
if not os.path.exists(result_path):
os.makedirs(result_path)
with open(os.path.join(root_path, dataset, 'groundtruth_rect.txt'), 'r') as f:
gts = f.readlines()
base_gt = gts[0].replace('\n', ' ')
base_gt = base_gt.replace('\t', ' ')
base_gt = re.sub(' +', ' ', base_gt)
if ',' in base_gt:
base_gt = base_gt.split(',')
else:
base_gt = base_gt.split(' ')
x,y,w,h = int(base_gt[0]),int(base_gt[1]),int(base_gt[2]),int(base_gt[3])
imgs_path = sorted(os.listdir(os.path.join(root_path, dataset, 'img')))
frame = cv2.imread(os.path.join(root_path,dataset, 'img', imgs_path[0]))
# roi = cv2.selectROI(windowName="roi", img=frame, showCrosshair=True, fromCenter=False)
# x,y,w,h = roi
h_img, w_img, c = frame.shape
temp = frame[y:y+h, x:x+w]
center_x = x+w/2
center_y = y+h/2
rect = [x,y,w,h]
m_weight = np.zeros((h, w))
hh = (w/2)*(w/2) + (h/2)*(h/2)
for i in range(h):
for j in range(w):
dist = (i-h/2)*(i-h/2) + (j-w/2)*(j-w/2)
m_weight[i][j] = 1-dist/hh
C = 1/sum(sum(m_weight))
hist1 = np.zeros((4096))
for i in range(h):
for j in range(w):
q_r = math.floor(float(temp[i][j][0])/16)
q_g = math.floor(float(temp[i][j][1])/16)
q_b = math.floor(float(temp[i][j][2])/16)
q_temp = q_r*256+q_g*16+q_b
hist1[q_temp] = hist1[q_temp] + m_weight[i][j]
hist1 = hist1*C
rect[2] = math.ceil(rect[2])
rect[3] = math.ceil(rect[3])
q_temp1 = np.zeros((h,w))
num_frame = 0
center_list = []
iou_list = []
for path in imgs_path:
base_gt = gts[num_frame].replace('\n', ' ')
base_gt = base_gt.replace('\t', ' ')
base_gt = re.sub(' +', ' ', base_gt)
if ',' in base_gt:
base_gt = base_gt.split(',')
else:
base_gt = base_gt.split(' ')
frame = cv2.imread(os.path.join(root_path, dataset, 'img', path))
num = 0
Y = [2,2]
num_frame += 1
while (Y[0]*Y[0]+Y[1]*Y[1]) > 0.5 and num < 20:
num += 1
temp1 = frame[int(rect[1]):int(rect[1]+rect[3]), int(rect[0]):int(rect[0]+rect[2])]
hist2 = np.zeros((4096))
for i in range(h):
for j in range(w):
q_r = math.floor(float(temp1[i][j][0]) / 16)
q_g = math.floor(float(temp1[i][j][1]) / 16)
q_b = math.floor(float(temp1[i][j][2]) / 16)
q_temp1[i][j] = q_r * 256 + q_g * 16 + q_b
hist2[int(q_temp1[i][j])] = hist2[int(q_temp1[i][j])] + m_weight[i][j]
hist2 = hist2*C
ww = np.zeros((4096))
for i in range(4096):
if hist2[i] != 0:
ww[i] = math.sqrt(hist1[i]/hist2[i])
else:
ww[i] = 0
#尝试更新hist1
# alpha = 0.998
# hist1 = alpha*hist1+(1-alpha)*hist2
sum_w = 0
xw = np.array([0.0,0.0])
for i in range(h):
for j in range(w):
sum_w += ww[int(q_temp1[i][j])]
xw += ww[int(q_temp1[i][j])]*np.array([i-h/2-0.5, j-w/2-0.5])
Y = xw/sum_w
rect[0] = rect[0]+Y[1]
rect[1] = rect[1]+Y[0]
if rect[0] < 0:
rect[0]= 0
if rect[1] < 0:
rect[1] = 0
if (rect[0]+rect[2]) > w_img:
rect[0] = rect[0]-((rect[0]+rect[2])-w_img)
if (rect[1]+rect[3]) > h_img:
rect[1] = rect[1]-((rect[1]+rect[3])-h_img)
cv2.rectangle(frame, (int(rect[0]),int(rect[1])), (int(rect[0]+rect[2]), int(rect[1]+rect[3])), (0, 255, 0), 2)
cv2.rectangle(frame, (int(base_gt[0]),int(base_gt[1])), (int(base_gt[0])+int(base_gt[2]), int(base_gt[1])+int(base_gt[3])), (0, 0, 255), 2)
cv2.putText(frame, "#{}".format(num_frame), (45, 45), cv2.FONT_HERSHEY_SIMPLEX, 1.2, (0, 0, 255), 2)
cv2.imwrite(result_path+'{:0>5d}.jpg'.format(num_frame), frame)
boxA = [int(rect[0]),int(rect[1]), int(rect[0]+rect[2]), int(rect[1]+rect[3])]
centerA = [int(int(rect[0])+int(rect[2])/2),int(int(rect[1])+int(rect[3])/2)]
centerB = [int(int(base_gt[0])+int(base_gt[2])/2),int(int(base_gt[1])+int(base_gt[3])/2)]
boxB = [int(base_gt[0]),int(base_gt[1]), int(base_gt[0])+int(base_gt[2]), int(base_gt[1])+int(base_gt[3])]
center_list.append(center_dis(centerA, centerB))
iou_list.append(axis_aligned_iou(boxA, boxB))
# print(np.mean(np.array(center_list)))
# print(np.mean(np.array(iou_list)))
# result.write(dataset+':'+str(np.mean(np.array(center_list)))+' '+str(np.mean(np.array(iou_list)))+'\n')
# result.close()
cv2.imshow('imgs', frame)
k = cv2.waitKey(1) & 0xff
if k == 27:
break
#保存结果图
# plt.plot(np.arange(len(center_list)), np.array(center_list), label=dataset)
# plt.legend()
# plt.xlabel('frame')
# plt.ylabel('center distance')
# # plt.show()
# plt.savefig('bad_center_list.png')
# plt.close()
#
# plt.plot(np.arange(len(iou_list)), np.array(iou_list), label=dataset)
# plt.legend()
# plt.xlabel('frame')
# plt.ylabel('iou')
# plt.show()
# plt.savefig('bad_iou_list.png')
# plt.close()参考：
https://blog.csdn.net/jinshengtao/article/details/30258833
https://www.cnblogs.com/ywsoftware/p/4434595.html