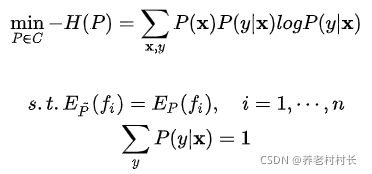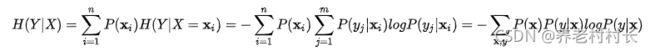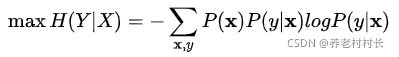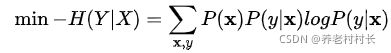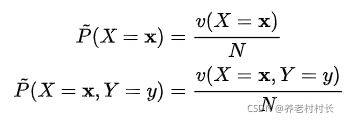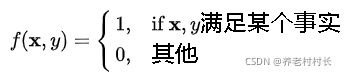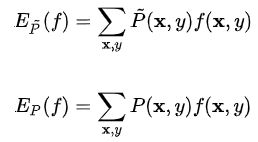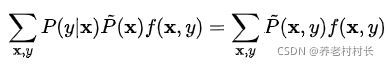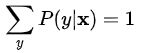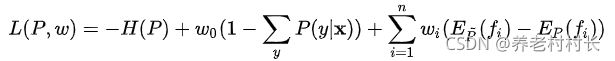【机器学习】最大熵模型
1. 思想
假设所有未知的事件出现概率都相等,在有约束的条件下求最优解。
2. 解释
在投骰子的案例中,我们知道骰子有六个面,若我们不知道骰子每个面朝上的概率,那么最安全的选择是假设每个面朝上的概率都相等,即1/6,这样保留了所有的可能性,确保了最大的不确定性。这样的原理就是最大熵原理,将该原理应用到分类得到找出最大熵模型,也是最好的分类模型。
3. 数学表达
3.1 公式
3.2 解释
3.2.1 最大熵原理
在信息论中,熵用于表示随机变量的不确定性大小,熵越大,不确定性则越大。假设离散型随机变量X的概率分布是 P(X),那么它的熵为:
关于熵的解释可以看笔者的另一篇文章。传送门:熵和KL散度
若每个P(X)都是等可能的,即P(X) = 1/N,则此时H(X) = - logP(X)
第一个式子表示的是最小化给定X后Y的负的条件熵,换句话说,最大化条件熵。
说说条件熵。假设 Y是一个离散型随机变量,在已知 X的条件下,那么定义 Y 的条件熵为:
可能比较抽象,简单举个例子会容易理解些,现有X = {x1=下雨, x2=不下雨},Y = {y1=出去玩,y2=不出去玩},在已知X的条件下,Y的条件熵H(Y|X) = P(X=x1)H(Y|X=x1) + P(X=x2)H(Y|X=x2)。直观上理解这步操作将数据集划分成了两份,一份和x1有关,一份和x2有关,分别计算这两份数据集下y的熵,也就是条件熵。这点和决策树一样,决策树通过计算在已知某个特征的情况下,Y的条件熵,从而计算信息增益,进而找到最优特征进行分枝。
有了目标函数后,现在需要最大化条件熵H(Y|X),也就有了如下式子:
通常,我们会将最大化问题转化为最小化问题,从而推导出3.1中的第一个式子:
3.2.2 经验分布和特征函数
根据贝叶斯公式,我们知道后验分布=联合分布/边缘分布,即
转换得到:
![]()
通过我们手中的数据集,该式子中P(X)和P(X|Y)P(Y)是可以得知的,被称为经验分布,P(Y|X)是未知的,也是我们要拟合的目标分布。
给定一个训练数据集![]() ,我们希望能借助最大熵原理从该数据集中学习到最好的分类模型。
,我们希望能借助最大熵原理从该数据集中学习到最好的分类模型。
我们可以从数据集中得到 ![]() 和
和![]() 的经验分布,其中v(X=x)表示样本x出现的频数, 表示样本数:
的经验分布,其中v(X=x)表示样本x出现的频数, 表示样本数:
往往在真实分布未知的情况下,我们会用经验分布去近似。后验分布![]() 即我们最后得到的近似真实分布的分布。
即我们最后得到的近似真实分布的分布。
我们通过观察数据集往往能发现一些事实,例如在一份扔骰子的数据集中,我们发现6朝上占比为 1/6;再例如一份关于天气的数据集中,我们发现湿度高且多云的天气下,几乎都会下雨。对于这些观察到的事实,往往采用特征函数去表示:
接着可以通过这些观察到的事实去约束模型,先定义特征函数关于经验分布![]() 的期望值
的期望值![]() 和关于联合分布
和关于联合分布![]() 的期望值
的期望值![]()
我们自然希望通过经验分布得到的联合分布(包含后验分布P(Y|X)和经验分布P(X))。如果模型能够获取训练数据中的信息,那么久可以假设这两个期望值相等,即
或
这是我们的约束条件,即3.1中的第二个式子。
可以发现,两边的未知量只有![]() 。就这样我们得到了最大熵模型中的约束条件,这些约束条件约束了可选的概率模型集合,假设满足所有约束条件的模型集合为:
。就这样我们得到了最大熵模型中的约束条件,这些约束条件约束了可选的概率模型集合,假设满足所有约束条件的模型集合为:
最后因为概率之和等于1,再添加多一个约束条件:
这也是3.1中的最后一个式子。
3.3 求解最大熵模型
可以定义该问题为有约束的优化问题,这类问题通常可用拉格朗日乘数法解决,通过引入拉格朗日乘数w,得到拉格朗日函数![]() ,有:
,有:
代入具体式子:
在拉格朗日乘数法中,最优化的初始问题为
对偶问题为
在本案例中,初试问题的解等于对偶问题的解,即上述两式相等。详细展开可以看一下凸优化的相关文章。
在将原始问题转换为对偶问题后,开始求解。
首先对![]() 偏导,求偏导为0的P(Y|X)。 如下:
偏导,求偏导为0的P(Y|X)。 如下:
本例中,关于![]() 的函数虽然有很多累加符号,但实际上我们一次只对其中的一个P(y|x)求偏导,其他与之无关的变量都可看做常数在求偏导后被消去。
的函数虽然有很多累加符号,但实际上我们一次只对其中的一个P(y|x)求偏导,其他与之无关的变量都可看做常数在求偏导后被消去。
4. 求解后的最大熵模型
在3.3中,我们通过推导得到了我们需要的后验分布P(Y|X),大家仔细看看这个式子,是不是有一种熟悉感?
没错,这个式子就是逻辑回归的原函数,sigmoid函数,逻辑回归为什么用sigmoid函数来作为激活函数?因为这是通过最大熵模型求解出来的。