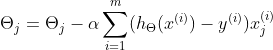基于Python的非线性回归(Logistic Regression)模型分析与应用
一、概率
1.定义:概率(P)robability ,衡量一件事情发生的可能性
2.范围:0<=P<=1
3.计算方法: 根据个人置信
根据历史数据
根据模拟数据
4.条件概率
二、Logistic Regression(逻辑回归)
1.由于现实中的具体事例的发生较为复杂,并不能应用线性的模型进行分析,如果要使用的话,就会再每次调整参数得时候同时要调整阈值的范围,那模型的普适性就会变差。因此,针对上述会出现的问题,我们选择了了逻辑回归模型进行分析。
2.逻辑回归的基本模型
假设要测试的数据为X(x0,x1,x2……xn)
对应上述测试数据要学习的参数为:
![]()
则得到如下的模型:![]()
对应的向量表示为:![]()
其中![]() 表示学习的参数的一维行向量,X为测试数据的一维行向量。
表示学习的参数的一维行向量,X为测试数据的一维行向量。
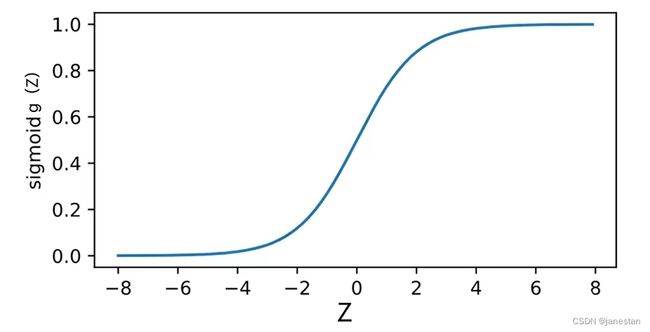
为了更好的处理上述的数据,我们引入了Sigmoid函数,这样可以使得我们的函数曲线变得平滑,即:
如上图所示为Sigmoid函数的图像,函数的值域范围为(0,1),且在自变量z取到0时,因变量g(Z)的值为1/2。
其中X为自变量,即预测数据值。![]() 为要学习的参数值。
为要学习的参数值。
与此同时,我们也可以将上述的函数改写为概率形式:
当所选的例子为正例(y=1):
![]()
当所选的例子为反例(y=0):
![]()
3.构造目标函数(Cost函数)
3.1线性回归
即总共有m个实例,![]() 代表实例的真实值,
代表实例的真实值,![]() 代表预测值 。
代表预测值 。
![]()
即找到满足上式最小的两个参数值。
3.2 Logistic regression
3.2.1Cost函数
3.2.2函数目标是找到满足上式最小的两个参数值
3.4解决方案:梯度下降法(gradient decent)
梯度下降法(Gradient descent,简称GD)是一阶最优化算法。 要使用梯度下降法找到一个函数的局部极小值,必须向函数上当前点对应梯度(或者是近似梯度)的反方向的规定步长距离点进行迭代搜索。如果相反地向梯度正方向迭代进行搜索,则会接近函数的局部极大值点,这个过程则被称为梯度上升法。
梯度下降法是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降法和最小二乘法是最常采用的方法。在求解损失函数的最小值时,可以通过梯度下降法来迭代求解,得到最小化的损失函数和模型参数值。反过来,如果我们需要求解损失函数的最大值,这时就需要用梯度上升法来迭代了。在机器学习中,基于基本的梯度下降法发展了两种常用梯度下降方法,分别为随机梯度下降法和批量梯度下降法。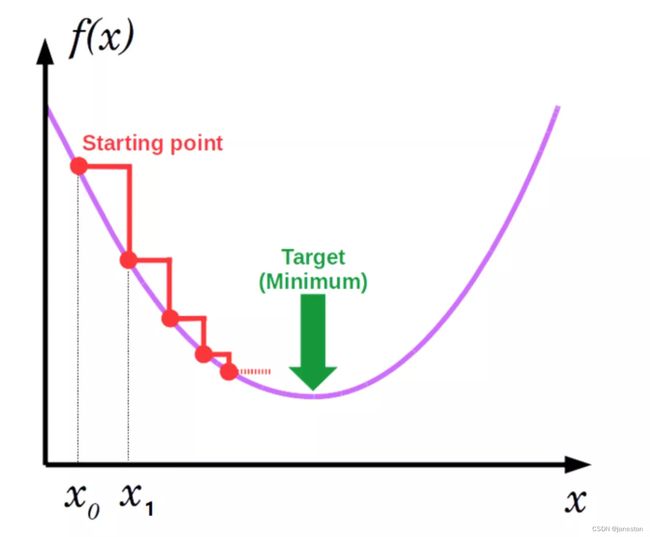
如上图所示就是一个梯度下降法的具体图示。即从某一点开始,选择对应的步长和方向进行,不断的下降,直到到达最终的最小值(可能是局部最小也可能是全局最小)为止。
更新法则:
其中![]() 为学习率,通过更新法则对所有的
为学习率,通过更新法则对所有的![]() 进行更新,重复更新直到所求结果达到提前设置的阈值或者更新值收敛为止。
进行更新,重复更新直到所求结果达到提前设置的阈值或者更新值收敛为止。
4.应用实例
import numpy as np
import random #生成随机数包
def genData(numPoints, bias, variance): #定义测试数据genData,实例,偏差,方差
x = np.zeros(shape=(numPoints, 2)) #行为numPonints,列为2
y = np.zeros(shape=(numPoints))
for i in range(0, numPoints): #等价于(0,numPoints-1)
x[i][0] = 1 #第一行都为1
x[i][1] = i #第二行的第几列就为几
y[i] = (i+bias)+random.uniform(0, 1)+variance #random.unoform(0,1)表示在(0,1)之间随机产生一个数
return x, y
def gradientDescent(x, y, theta, alpha, m, numIterations): #定义梯度下降法
xTran = np.transpose(x) #求解X的转置矩阵
for i in range(numIterations):
hypothesis = np.dot(x, theta)
loss = hypothesis-y
cost = np.sum(loss**2)/(2*m) #所使用的是最简单的Cost函数表达式,并非这节内容中的Cost函数表达式
gradient=np.dot(xTran, loss)/m #求解梯度函数
theta = theta-alpha*gradient
print("Iteration %d | cost :%f" % (i, cost))
return theta
x,y = genData(80, 20, 10) #生成一个2行80列,每列偏差为20,方差为10的一组测试数据
print("x:")
print(x)
print("y:")
print(y)
m, n = np.shape(x)
n_y = np.shape(y)
print("m:"+str(m)+" n:"+str(n)+" n_y:"+str(n_y))
numIterations = 100000
alpha = 0.0005
theta = np.ones(n)
theta = gradientDescent(x, y, theta, alpha, m, numIterations)
print(theta)运行结果:
[30.54631528 0.99893825]
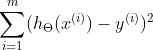
![J(\Theta )=\frac{1}{m}Cost(h_{\Theta }(x^{(i)}),y^{(i)})=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}log(h_{\Theta }(x^{(i)}))+(1-y^{(i)}log(1-h_{\Theta }x^{(i)}))]](http://img.e-com-net.com/image/info8/072d6abb392e45c0aadced07bd5b77e4.gif)