LightGBM原理简介

1. LightGBM简介

        Light Gradient Boosting Machine 是一个实现GBDT算法的框架，支持高效率的并行训练，并且具有以下优点：

1. 更快的训练速度；

2. 更低的内存消耗；

3. 更好的准确率；

4. 分布式支持，可以快速处理海量数据。

1.1 GBDT的不足

        GBDT在每一次迭代的时候，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据，普通的GBDT算法是不能满足其需求的。

        LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题，让GBDT可以更好更快地用于工业实践。

1.2 相比于XGBoost的优化

1. 基于Histogram的决策树算法；

2. 带深度限制的Leaf-wise的叶子生长策略；

3. 直方图做差加速直接；

4. 支持类别特征(Categorical Feature)；

5. Cache命中率优化；

6. 基于直方图的稀疏特征优化多线程优化。

2. LightGBM的优化点

 参考：LightGBM模型的特点和优点

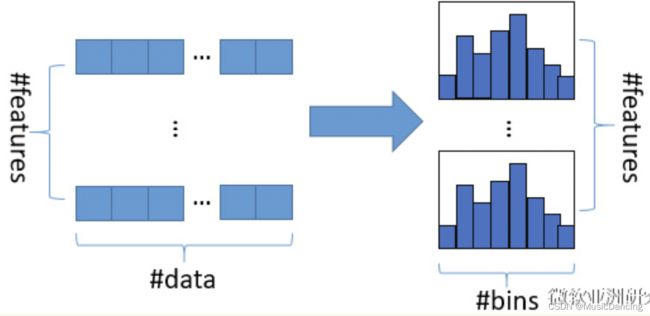
2.1 使用直方图的方式

        基本思想：先把连续的浮点特征值离散化成k个整数（其实就是分桶的思想，而这些桶称为bin，比如[0,0.1)→0, [0.1,0.3)→1），同时构造一个宽度为k的直方图。在遍历数据的时候，根据离散化后的值作为索引在直方图中累积统计量，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点。

 优点：

1. 内存消耗的降低：直方图算法不仅不需要额外存储预排序的结果，而且可以只保存特征离散化后的值，而这个值一般用8位整型存储就足够了，内存消耗可以降低为原来的1/8。

2. 计算代价也大幅降低：预排序算法每遍历一个特征值就需要计算一次分裂的增益，而直方图算法只需要计算k次（k可以认为是常数），时间复杂度从O(#data#feature)优化到O(k#features)。

        对于每个特征的所有候选分割点按照其范围分成N个箱子，累加箱子内的梯度提升值，对于箱子里的每个候选分割点都计算带来的梯度增益，对于每个箱子分别保存其累计梯度、箱子内的样本数量，之后再分裂节点时直接对直方图遍历进行分割点的候选即可。

        通过直方图的方式，虽然分割的精度变差了，但是对最后的结果影响不大，一方面能够提升计算效率，另一方面这种较粗的分割点可以起到一种正则化的效果。

        之后进行结点分裂时候，只需要根据梯度之和计算loss即可。 看来对Gain增益的计算在梯度计算中。

 2.2 直方图做差加速

        一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图，需要遍历该叶子上的所有数据，但直方图做差仅需遍历直方图的k个桶。利用这个方法，lgb在构造一个叶子的直方图后（父节点在上一轮就已经计算出来了），可以用非常微小的代价得到它兄弟叶子的直方图，在速度上可以提升一倍。        

        

2.3 使用GOSS 基于梯度的单边采样方法

goss是样本采样。

基本思想：梯度大的样本点在信息增益的计算上扮演着主要的作用，也就是说这些梯度大的样本点会贡献更多的信息增益，因此为了保持信息增益评估的精度，当我们对样本进行下采样的时候保留这些梯度大的样本点，而对于梯度小的样本点按比例进行随机采样即可。   

        也就是会分别计算样本所带来的梯度变化，下次再构建树时候，完全使用梯度大的样本，而对梯度小的进行随机采样，这样可以简化模型，提升速度，起到一种抗过拟合的效果。

2.4 EFB互斥特征捆绑算法

        EFB是一种特征抽样，来进一步提升训练速度，将互斥的特征捆绑在一起来减少特征维度。高维度的数据通常是非常稀疏的，特征空间的稀疏性让我们可以设计一个几乎无损的方法去减少特征的数量。

        具体来说，在稀疏的特征空间中，许多特征是互斥的，它们从不同时取非零值。所以可以安全地将互斥特征捆绑到一个特征中（称之为exclusive feature bundle）。通过仔细地设计特征扫描算法，可以像独立特征一样给feat bundles建立feature histograms。

这里的核心是不同时取非0值的，可以绑成一个特征，也就是会让新的特征大部分都是非0值。

2.5 带深度限制的Leaf-wise机制

1. level-wise的优缺点

        在XGBoost中，树是按层生长的，称为Level-wise tree growth，同一层的所有节点都做分裂，最后剪枝，如下图所示：

        Level-wise过一次数据可以同时分裂同一层的叶子，容易进行多线程优化，也好控制模型复杂度，不容易过拟合。但实际上Level-wise是一种低效的算法，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销，因为实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。

2. leaf-wise的改进

        Leaf-wise叶子生长策略是一种更为高效的策略，每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。因此同Level-wise相比，在分裂次数相同的情况下，Leaf-wise可以降低更多的误差，得到更好的精度。

        Leaf-wise的缺点是可能会长出比较深的决策树，产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合。

2.6 直接支持类别型特征

        优化了对类别特征的支持，不需要做one-hot编码，提高了空间和时间的效率。并在决策树算法上增加了类别特征的决策规则。

        在Expo数据集上的实验，相比one-hot展开的方法，训练速度可以加速8倍，并且精度一致。利用了分箱的机制。它也是第一个直接支持类别特征的GBDT工具。

2.7 支持高效并行计算

2.7.1 特征并行

        特征并行的主要思想是在不同机器、不同的特征集合上分别寻找最优的分割点，然后在机器间同步最优的分割点。

 2.7.2 数据并行

        数据并行则是让不同的机器先在本地构造直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点。

5. 常见题目

1. GBDT中的梯度是什么，对什么的梯度？

梯度就是看对谁求导，lr是对w求导，gbdt是对F(xi)求导。

是loss(yi,F(xi)) 对当前模型(之前拟合的所有轮次tree的和)在训练集样本上的预测值的梯度；

对F(xi)求导，其中F(xi)是当前模型所有树预测值的和。

当前training example所贡献的那一小点loss，对当前F(xi)的梯度

GBM里第m步，根据泰勒一阶展开， "伪残差"是loss关于(x)的负一阶导L'|f=(x)，GBDT里是上一步拟合残差(x, r_m)后生成的回归树。

2. 给一个有m个样本，n维特征的数据集，如果用LR算法，那么梯度是几维？

n+1维，还有个bias啊

对单样本x，LR的loss=(y- sigmoid(w*x+b))^2，关于w求导后: 2*(y-sigmoid(wx+b))*x，维数和输入一样， 也就是n。

3. 同样的m*n数据集，如果用GBDT，那么梯度是几维？m维？n维？m*n维？或者是与树的深度有关？或者与树的叶子节点的个数有关？

        每一轮都需要对m个样本求梯度，所以梯度是m维。每轮迭代都会对所有样本的f(xi)求导，取负数梯度得到r_ti，这样低t轮就得到(xi,r_ti) i=1...m，对这些数据拟合一颗CART树，再求权重。

        本身的梯度是和F(xi)有关的，也就是和树的结构有关。只是在计算loss的时候把所有样本累加了，并不是说梯度的维度就是m。

梯度不能叫维度吧，有多少个还差不多，m个而已

跟样本点数量一样（y1, y2,...ym） 离散的函数

是当前损失函数对当前和函数"在样本点处"求梯度

3 m维，还有就是gbdt在一阶泰勒展开后需要添加正则化以防止naive solution，而xgb展开到二阶后，如果cost function的二阶导数大于0，相当于某种意义上的自带正则

第三问的答案我觉得应该是跟叶子节点个数有关，计算梯度需要遍历m个样本没错，但不意味着m个样本每个都对应一个维度。事实上每一个梯度对应的其实是一个参数的更新，gbdt里的参数个数是由叶子数决定的，所以梯度个数应该是跟叶子节点数有关。