【论文阅读】Towards Time-Aware Knowledge Graph Completion
Towards Time-Aware Knowledge Graph Completion
重点:知识图谱中考虑时间因素time实现知识图谱的补全。
框架
模型
1) Time-Aware Embedding Task Model
对于任意正向训练四元组 ( e i , r k , e j , t r k ) (e_i,r_k,e_j,t_{r_k}) (ei,rk,ej,trk),具有相同的头实体和相应的时间顺序关系对 ( r k , r l ) (r_k,r_l) (rk,rl),可以找到一个相关的四元组 ( e i , r l , e m , t r l ) (e_i,r_l,e_m,t_{r_l}) (ei,rl,em,trl),对于相应的事件顺序关系对,定义时间评分函数:

2) Time-Aware KG Completion
引入时间因素约束,时间因素约束分为三种:
1)时间间隔约束
2)时间顺序约束
3)时间不重叠约束
总目标函数:
m a x ∑ x i j ( k ) w i j ( k ) x i j ( k ) max\sum_{x_{ij}^{(k)}}w_{ij}^{(k)}x_{ij}^{(k)} maxxij(k)∑wij(k)xij(k)
- w i j ( k ) = f ( e i , r k , e j ) w_{ij}^{(k)}=f(e_i,r_k,e_j) wij(k)=f(ei,rk,ej) 四元组满足嵌入约束
- x i j ( k ) x_{ij}^{(k)} xij(k) Boolean decision variable,四元组满足时间约束
目标:找到一个最优解 x i j ( k ) x_{ij}^{(k)} xij(k)
进一步
1)Time-Aware KG Completion Task(时序知识图谱补全任务)
四元组表示 ( e i , r , e j , t ) (e_i,r,e_j,t) (ei,r,ej,t): e i e_i ei和 e j e_j ej在时间间隔 t = [ t b , t e ] t=[t_b,t_e] t=[tb,te]上存在关系r
当事情发生的很快非连序时, t b = t e t_b=t_e tb=te,当事情还没结束一直发生时, t = [ t b , + ∞ ] t=[t_b,+\infty] t=[tb,+∞]
时序知识图谱补全任务:给定一个特定的事件间隔t,补全缺失的四元组,缺失 e i , r 或 e j e_i,r或e_j ei,r或ej
2)和普通的知识图谱嵌入相比,时序知识图谱嵌入、
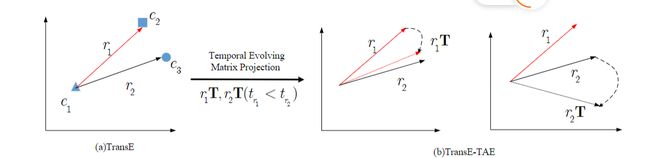
TransE假设每个关系是时间独立的,为了更好地建模知识演化,假设时间有序关系相互关联并在时间维度上演化
比如:一个人从出生到死亡,wasBorn -> graduationedFrom -> diedIn
定义:temporal ordering relation pair, 定义一个共享同一个头部实体的时间排序关系 < wasBornIn,diedIn >,之前的关系是先验关系,其他是后继关系。正样本:< prior relaiton ,subsequent relation >,负样本:< subsequent relation , prior relation>
定义:时间演化矩阵 T ∈ R n × n T \in R^{n \times n} T∈Rn×n,n是关系嵌入的维度,假设prior relation 可以通过T转换为subsequent relation,有 r 1 T ≈ r 2 r_1T \approx r_2 r1T≈r2,但是 r 2 T r_2T r2T远离 r 1 r_1 r1.
进一步,将时序知识图谱补全可以定义为:
给定任意正样本四元组 ( e i , r k , e j , t r k ) ∈ Δ t (e_i,r_k,e_j,t_{r_k}) \in\Delta_t (ei,rk,ej,trk)∈Δt,可以找到一个时序相关的四元组 ( e i , r l , e m , t r l ) ∈ Δ t (e_i,r_l,e_m,t_{r_l}) \in \Delta_t (ei,rl,em,trl)∈Δt共享一个相同的头实体和一个时间顺序关系对 < r k , r l > < r_k,r_l > <rk,rl>,如果 t r k < t r l t_{r_k}
定义:正样本时间顺序关系对拥有更低的得分。
g ( < r k , r l > ) = ∥ r k T − r l ∥ l 1 / l 2 g(
使用共同尾实体的时序关系可以通过其逆关系并且互换头尾实体来完成
联合得分函数:
L = ∑ x + ∈ Δ [ ∑ x − ∈ Δ − [ γ 1 + f ( x + ) − f ( x − ) ] + ] + λ ∑ y + ∈ Ω e i , t r k , y − ∈ Ω e i , t r k − [ γ 2 + g ( y + ) − g ( y − ) ] + L=\sum_{x^+\in \Delta}[\sum_{x^-\in {\Delta^-}}[\gamma_1+f(x^+)-f(x^-)]_+] + \lambda \sum_{y^+ \in \Omega_{e_i,t_{r_k}},y^- \in \Omega_{e_i,t_{r_k}}^-}[\gamma_2+g(y^+)-g(y^-)]_+ L=x+∈Δ∑[x−∈Δ−∑[γ1+f(x+)−f(x−)]+]+λy+∈Ωei,trk,y−∈Ωei,trk−∑[γ2+g(y+)−g(y−)]+
L a l l = L k g + L t i m e L_{all}=L_{kg}+L_{time} Lall=Lkg+Ltime
前一项是求embedding嵌入,后一项是要求嵌入空间在时间上保持一致。
3)时序知识图谱加入时序约束
定义: w i j ( k ) = f ( e i , r k , e j ) w_{ij}^{(k)}=f(e_i,r_k,e_j) wij(k)=f(ei,rk,ej)表示预测的正确性。引入 x i j ( k ) x_{ij}^{(k)} xij(k)指出四元组 ( e i , r k , e i , t ) (e_i,r_k,e_i,t) (ei,rk,ei,t)在时间间隔内是否是正确的,是一个布尔决策变量
目标函数:
J = ∑ x i j ( k ) w i j ( k ) x i j ( k ) J=\sum_{x_{ij}^{(k)}}w_{ij}^{(k)}x_{ij}^{(k)} J=xij(k)∑wij(k)xij(k)
约束:
1)时间不相交约束,相同头实体,相同关系,不同时间间隔
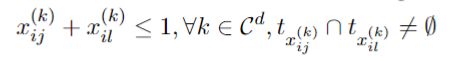
2)时间顺序依赖
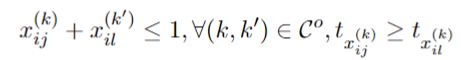
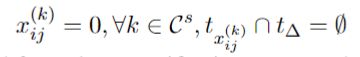
整数线性规划目标:找到最优解 x i j ( k ) x_{ij}^{(k)} xij(k)
如何应用
对于需要补全的四元组 ( e i , ? , r k , t r k ) (e_i,?,r_k,t_{r_k}) (ei,?,rk,trk),依次替换e_j,得到n个四元组,判断那个四元组是正确四元组。
需要满足1) f ( i , j , r ) 评分越大 f(i,j,r)评分越大 f(i,j,r)评分越大 2)时序性约束 X i j ( k ) X_{ij}^{(k)} Xij(k)为真。
进一步满足 M a x ∑ x i j ( k ) w i j ( k ) x i j ( k ) Max\sum_{x_{ij}^{(k)}}w_{ij}^{(k)}x_{ij}^{(k)} Max∑xij(k)wij(k)xij(k)
同时满足上诉3个约束条件
使用整数线性规划方法,得到最符合要求的四元组
整数线性规划
形如:
max z=10x+20y
约束条件
{
5x+4y<=24,
x,y>=0,
x,y是整数 ,
// 约束条件指定为整数
}
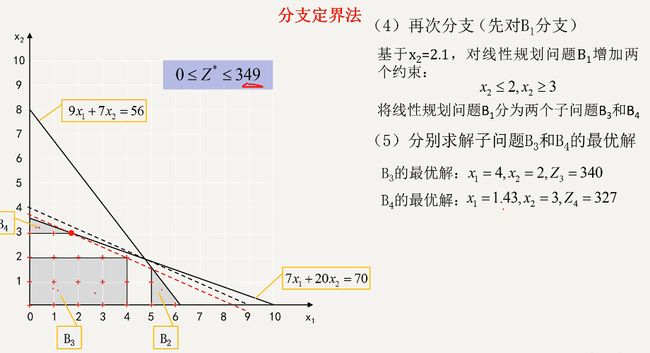
分支定界法
最优目标函数值: z ∗ z^* z∗
原理:不断将线性规划问题B的可行域分为子区域,逐步搜小 z ∗ z^* z∗的上界和下界
上下界更新:问题B各分支最优目标函数的最大值作为新的上界,在已求出整数条件的解中的最大者作为新的下界
求解步骤:
- 初始定界:求解对应线性规划问题B的最优解,作为初始上届,求解整数线性规划问题A的一个整数解,作为初始下届。
- 分支:选择B最优解中不满足整数条件的变量,添加约束将B分为两个子问题B1,B2,不考虑整数约束求解B1,B2的最优解
- 定界:比较各分支的解,将最优目标函数值的最大值作为上届,各个分支满足整数条件的解中的最大者作为下届
- 剪支:比较各个分支的解,若小于新的下届,剪枝,若无可行解,剪枝,若大于新的下届,重复2,3,4。