【Python深度学习】Python全栈体系（三十三）

深度学习

第十四章 PaddlePaddle 概览

一、PaddlePaddle 简介

1. 什么是 PaddlePaddle ？

• PaddlePaddle （Parallel Distributed Deep Learning，中文名飞桨）是百度公司推出的开源，易学习，易使用的分布式深度学习平台
• 源于产业实践，在实际中有着优异表现
• 支持多种机器学习经典模型
  

2. 为什么学习 PaddlePaddle？

• 开源，国产
• 提供算力支持，能完成复杂的图像任务
• 程序简洁，使用较为简单，降低教学和学习难度

3. PaddlePaddle 优点

• 易用性。语法简介，API的设计干净清晰
• 丰富的模型库。借助于其丰富的模型库，可以非常容易的复现一些经典方法
• 全中文说明文档。首家完整支持中文文档的深度学习平台
• 运行速度快。充分利用 GPU 集群的性能，为分布式环境的并行计算进行加速

4. PaddlePaddle 缺点

• 教材少
• 行业应用较少

5. 国际竞赛获奖情况

6. 行业应用

二、体系结构

1. 总体架构

2. 编译时与执行时

3. 三个重要术语

• Fluid：定义程序执行流程
• Program：对用户来说是一个完整的程序
• Executor：执行器，执行程序

4. 代码

# paddlepaddle版本：1.5
import paddle.fluid as fluid

# 创建两个常量
x = fluid.layers.fill_constant(shape=[1], dtype="int64", value=5)
y = fluid.layers.fill_constant(shape=[1], dtype="int64", value=1)
z = x + y  # 执行两个常量的相加

# 创建执行器
place = fluid.CPUPlace()  # 指定程序在CPU上执行
exe = fluid.Executor(place)  # 创建执行器
result = exe.run(fluid.default_main_program(),
                 fetch_list=[z])  # 指定要返回的结果
print(result)
"""
[array([6], dtype=int64)]
"""

第十五章 基本概念与操作

基本概念

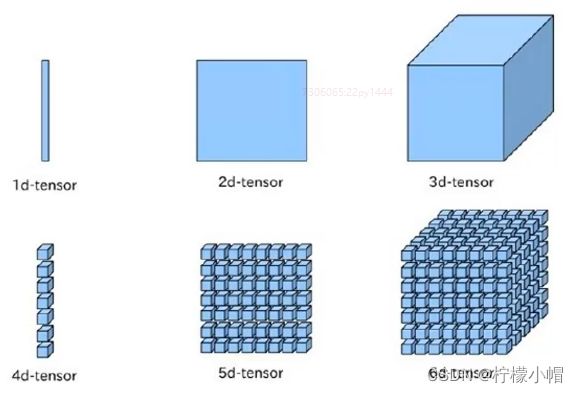
1. 张量

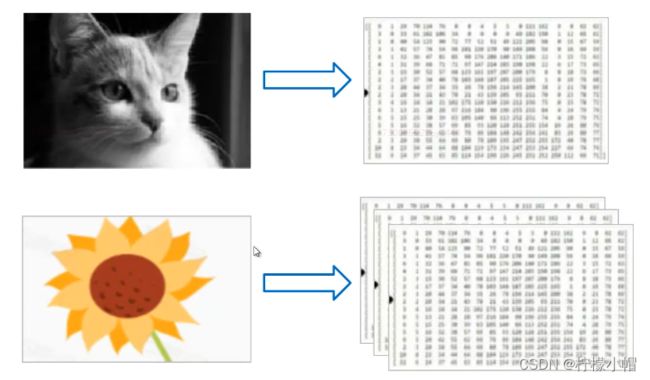
• 张量（Tensor）：多维数组或向量，同其它主流深度学习框架一样，PaddlePaddle使用张量来承载数据
  
• 灰度图像为二维张量（矩阵），彩色图像为三维张量
  

2. Layer

• 表示一个独立的计算逻辑，通常包含一个或多个operator（操作），如layers.relu表示ReLU计算；layers.pool2d表示pool操作。Layer的输入和输出为Variable。

3. Variable

• 表示一个变量，可以是一个张量（Tensor），也可以是其它类型。Variable进入Layer计算，然后Layer返回Variable。创建变量方式：
  

4. Program

• Program包含Variable定义的多个变量和Layer定义的多个计算，是一套完整的计算逻辑。从用户角度来看，Program是顺序、完整执行的。
  

5. Executor

• Executor用来接收并执行Program，会一次执行Program中定义的所有计算。通过feed来传入参数，通过fetch_list来获取执行结果。

outs = exe.run(fluid.default_main_program(), # 默认程序上执行
			   feed=params, # 喂入参数
			   fetch_list=[result]) # 获取结果

6. Place

• PaddlePaddle 可以运行在Intel CPU，Nvidia GPU，ARM CPU和更多嵌入式设备上，可以通过Place用来指定执行的设备（CPU或GPU）。

place = fluid.CPUPlace() 	 # 指定CPU执行
place = fluid.CUDAPlace(0) 	 # 指定GPU执行

7. Optimizer

• 优化器，用于优化网络，一般用来对损失函数做梯度下降优化，从而求得最小损失值

8. 代码

# 变量（张量）示例
import paddle.fluid as fluid
import numpy

# 创建两个变量，2行3列，类型为浮点型
x = fluid.layers.data(name="x", shape=[2, 3], dtype="float32")
y = fluid.layers.data(name="y", shape=[2, 3], dtype="float32")

x_add_y = fluid.layers.elementwise_add(x, y)  # 张量按元素相加
x_mul_y = fluid.layers.elementwise_mul(x, y)  # 张量按元素相乘

place = fluid.CPUPlace()  # 指定在CPU上执行
exe = fluid.Executor(place)  # 执行器
exe.run(fluid.default_startup_program())  # 初始化

a = numpy.array([[1, 2, 3],
                 [4, 5, 6]])
b = numpy.array([[1, 1, 1],
                 [2, 2, 2]])
params = {"x": a, "y": b}  # 参数字典
outs = exe.run(program=fluid.default_main_program(),  # 要执行的program
               feed=params,  # 执行program需要的参数
               fetch_list=[x_add_y, x_mul_y])  # 指定要获取的结果
print(numpy.array(outs).shape)
for i in outs:
    print(i)

"""
(2, 2, 3)
[[2 3 4]
 [6 7 8]]
[[ 1  2  3]
 [ 8 10 12]]
"""

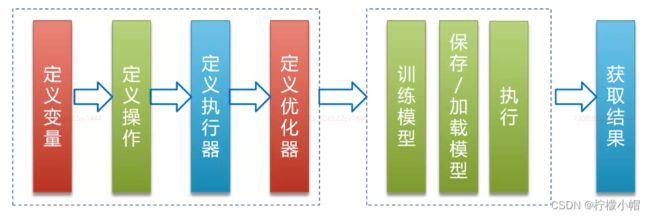
9. 程序执行步骤

第十六章 综合案例：实现线性回归

线性回归

1. 案例3：编写简单线性回归

2. 代码

# 简单线性回归
import paddle
import paddle.fluid as fluid
import numpy as np
import matplotlib.pyplot as plt

# 定义样本
train_data = np.array([[0.5], [0.6], [0.8], [1.1], [1.4]]).astype("float32")
y_true = np.array([[5.0], [5.5], [6.0], [6.8], [6.8]]).astype("float32")

# 定义变量
x = fluid.layers.data(name="x", shape=[1], dtype="float32")
y = fluid.layers.data(name="y", shape=[1], dtype="float32")

# 搭建模型，构建损失函数，优化器
y_predict = fluid.layers.fc(input=x,  # 输入数据
                            size=1,  # 输出值的个数
                            act=None)  # 激活函数，回归这里不采用激活函数

# 损失函数
cost = fluid.layers.square_error_cost(input=y_predict,  # 预测值
                               label=y)  # 真实值
avg_cost = fluid.layers.mean(cost) # 均方差
# 优化器
optimizer = fluid.optimizer.SGD(learning_rate=0.01) # 随机梯度下降优化器
optimizer.minimize(avg_cost) # 指定要优化的对象

# 执行器
place = fluid.CPUPlace()
exe = fluid.Executor(place)
exe.run(fluid.default_startup_program())

# 开始迭代训练
costs = []
iters = []
params = {"x":train_data, "y":y_true} # 参数字典

for i in range(200):
    outs = exe.run(feed=params, # 传入的参数
                   fetch_list=[y_predict.name, avg_cost.name])
    iters.append(i) # 记录迭代次数
    costs.append(outs[1][0]) # 记录损失值
    print("i: ", i, "cost: ", outs[1][0])

# 损失函数可视化
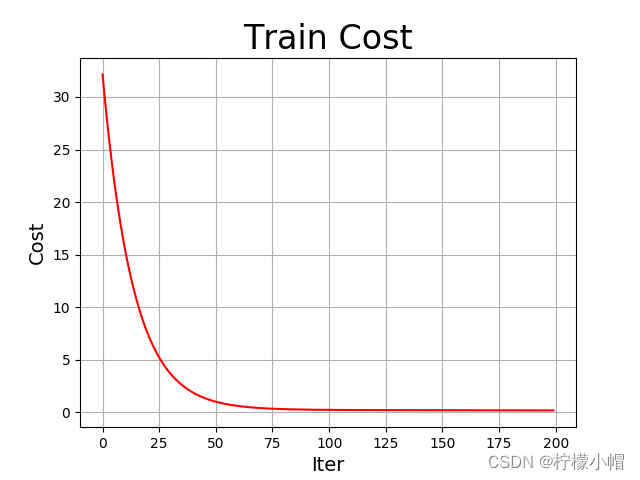
plt.figure("Training")
plt.title("Train Cost", fontsize=24)
plt.xlabel("Iter", fontsize=14)
plt.ylabel("Cost", fontsize=14)
plt.plot(iters, costs, color="red", label="Train Cost")
plt.grid()
plt.savefig("train.png") # 保存图片

# 线性模型可视化
tmp = np.random.rand(10, 1) # 生成10行1列的均匀的随机数组
tmp = tmp * 2 # 范围放大
tmp.sort(axis=0) # 排序
x_test = np.array(tmp).astype("float32")
params = {"x":x_test, "y":x_test} # y不参加计算，仅仅是为了避免语法错误
y_out = exe.run(feed=params,
                fetch_list=[y_predict.name]) # 返回预测结果
y_test = y_out[0]

plt.figure("Infer")
plt.title("Linear Regression", fontsize=24)
plt.plot(x_test, y_test, color="red", label="infer")
plt.scatter(train_data, y_true) # 绘制原始样本散点图

plt.legend()
plt.grid()
plt.savefig("infer.png")
plt.show()

"""
i:  0 cost:  32.14875
i:  1 cost:  29.862375
i:  2 cost:  27.739735
i:  3 cost:  25.769098
i:  4 cost:  23.939585
i:  5 cost:  22.24108
i:  6 cost:  20.664204
i:  7 cost:  19.200241
i:  8 cost:  17.841106
i:  9 cost:  16.579292
i:  10 cost:  15.4078245
i:  11 cost:  14.320238
i:  12 cost:  13.310519
i:  13 cost:  12.373095
i:  14 cost:  11.502786
i:  15 cost:  10.694782
i:  16 cost:  9.944625
i:  17 cost:  9.24817
i:  18 cost:  8.601569
i:  19 cost:  8.001253
i:  20 cost:  7.4439073
i:  21 cost:  6.9264526
i:  22 cost:  6.4460325
i:  23 cost:  5.999995
i:  24 cost:  5.5858774
i:  25 cost:  5.201392
i:  26 cost:  4.8444185
i:  27 cost:  4.5129848
i:  28 cost:  4.2052617
i:  29 cost:  3.9195523
i:  30 cost:  3.6542792
i:  31 cost:  3.4079788
i:  32 cost:  3.1792922
i:  33 cost:  2.9669576
i:  34 cost:  2.7698038
i:  35 cost:  2.5867443
i:  36 cost:  2.4167686
i:  37 cost:  2.2589402
i:  38 cost:  2.112389
i:  39 cost:  1.9763073
i:  40 cost:  1.8499448
i:  41 cost:  1.7326069
i:  42 cost:  1.6236455
i:  43 cost:  1.5224622
i:  44 cost:  1.4284992
i:  45 cost:  1.341239
i:  46 cost:  1.2602023
i:  47 cost:  1.1849433
i:  48 cost:  1.1150477
i:  49 cost:  1.0501318
i:  50 cost:  0.9898391
i:  51 cost:  0.9338385
i:  52 cost:  0.88182247
i:  53 cost:  0.8335059
i:  54 cost:  0.7886235
i:  55 cost:  0.74693
i:  56 cost:  0.7081963
i:  57 cost:  0.672211
i:  58 cost:  0.63877684
i:  59 cost:  0.60771143
i:  60 cost:  0.5788453
i:  61 cost:  0.5520208
i:  62 cost:  0.5270917
i:  63 cost:  0.5039226
i:  64 cost:  0.48238698
i:  65 cost:  0.46236864
i:  66 cost:  0.44375867
i:  67 cost:  0.42645583
i:  68 cost:  0.41036686
i:  69 cost:  0.39540488
i:  70 cost:  0.38148916
i:  71 cost:  0.36854538
i:  72 cost:  0.35650307
i:  73 cost:  0.34529853
i:  74 cost:  0.3348711
i:  75 cost:  0.3251656
i:  76 cost:  0.31613076
i:  77 cost:  0.30771756
i:  78 cost:  0.2998822
i:  79 cost:  0.29258323
i:  80 cost:  0.2857826
i:  81 cost:  0.27944416
i:  82 cost:  0.27353522
i:  83 cost:  0.268025
i:  84 cost:  0.2628848
i:  85 cost:  0.2580886
i:  86 cost:  0.25361156
i:  87 cost:  0.24943061
i:  88 cost:  0.24552512
i:  89 cost:  0.24187514
i:  90 cost:  0.2384623
i:  91 cost:  0.23526998
i:  92 cost:  0.23228231
i:  93 cost:  0.22948468
i:  94 cost:  0.22686367
i:  95 cost:  0.2244062
i:  96 cost:  0.22210129
i:  97 cost:  0.21993744
i:  98 cost:  0.21790509
i:  99 cost:  0.2159946
i:  100 cost:  0.21419752
i:  101 cost:  0.21250553
i:  102 cost:  0.2109113
i:  103 cost:  0.20940804
i:  104 cost:  0.20798898
i:  105 cost:  0.20664816
i:  106 cost:  0.20538029
i:  107 cost:  0.20417997
i:  108 cost:  0.20304254
i:  109 cost:  0.20196381
i:  110 cost:  0.20093882
i:  111 cost:  0.19996476
i:  112 cost:  0.19903736
i:  113 cost:  0.19815376
i:  114 cost:  0.1973104
i:  115 cost:  0.19650479
i:  116 cost:  0.19573417
i:  117 cost:  0.19499631
i:  118 cost:  0.19428857
i:  119 cost:  0.19360924
i:  120 cost:  0.1929558
i:  121 cost:  0.19232717
i:  122 cost:  0.19172087
i:  123 cost:  0.19113576
i:  124 cost:  0.19057044
i:  125 cost:  0.19002345
i:  126 cost:  0.18949324
i:  127 cost:  0.18897915
i:  128 cost:  0.1884798
i:  129 cost:  0.18799429
i:  130 cost:  0.18752147
i:  131 cost:  0.18706083
i:  132 cost:  0.18661138
i:  133 cost:  0.18617228
i:  134 cost:  0.18574297
i:  135 cost:  0.18532269
i:  136 cost:  0.18491097
i:  137 cost:  0.18450731
i:  138 cost:  0.18411079
i:  139 cost:  0.18372127
i:  140 cost:  0.18333833
i:  141 cost:  0.18296146
i:  142 cost:  0.18259028
i:  143 cost:  0.18222466
i:  144 cost:  0.18186378
i:  145 cost:  0.1815077
i:  146 cost:  0.18115589
i:  147 cost:  0.18080838
i:  148 cost:  0.18046463
i:  149 cost:  0.18012469
i:  150 cost:  0.17978814
i:  151 cost:  0.17945506
i:  152 cost:  0.17912471
i:  153 cost:  0.17879744
i:  154 cost:  0.17847298
i:  155 cost:  0.17815109
i:  156 cost:  0.17783158
i:  157 cost:  0.17751442
i:  158 cost:  0.17719956
i:  159 cost:  0.17688681
i:  160 cost:  0.17657606
i:  161 cost:  0.1762673
i:  162 cost:  0.17596017
i:  163 cost:  0.17565484
i:  164 cost:  0.17535129
i:  165 cost:  0.17504928
i:  166 cost:  0.17474873
i:  167 cost:  0.17444973
i:  168 cost:  0.1741523
i:  169 cost:  0.17385599
i:  170 cost:  0.17356104
i:  171 cost:  0.17326745
i:  172 cost:  0.17297497
i:  173 cost:  0.17268378
i:  174 cost:  0.17239359
i:  175 cost:  0.17210452
i:  176 cost:  0.17181674
i:  177 cost:  0.1715299
i:  178 cost:  0.1712438
i:  179 cost:  0.17095914
i:  180 cost:  0.17067508
i:  181 cost:  0.17039225
i:  182 cost:  0.17010994
i:  183 cost:  0.16982885
i:  184 cost:  0.16954863
i:  185 cost:  0.1692693
i:  186 cost:  0.16899088
i:  187 cost:  0.16871312
i:  188 cost:  0.16843624
i:  189 cost:  0.16816023
i:  190 cost:  0.16788514
i:  191 cost:  0.16761053
i:  192 cost:  0.16733672
i:  193 cost:  0.16706398
i:  194 cost:  0.16679177
i:  195 cost:  0.16652039
i:  196 cost:  0.1662497
i:  197 cost:  0.16597958
i:  198 cost:  0.16571043
i:  199 cost:  0.16544196


"""