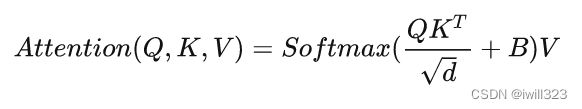李沐精读论文：Swin transformer: Hierarchical vision transformer using shifted windows

论文地址：Swin transformer: Hierarchical vision transformer using shifted windows

代码：官方源码

pytorch实现

SwinTransformerAPI

视频：Swin Transformer论文精读【论文精读】_哔哩哔哩_bilibili

本文注意参考：Swin Transformer论文精读【论文精读】 - 哔哩哔哩       

图解Swin Transformer - 知乎

        

目录

题目和摘要

引言      

ViT在视觉领域应用面临的问题

W-MSA 特点和好处

移动窗口的操作

展望

结论

方法

前向过程

代码框架

Patch Embedding：切出patch并做Embedding

Patch Merging：把临近的小 patch合并成一个大 patch

划分出包含patch的窗口

Window Attention

代码

Relative Position Bias：相关位置编码       

前向代码

W-MSA计算复杂度

移动窗口

提高移动窗口的计算效率

掩码可视化

代码  

Transformer Block整体架构

Block的前向代码   

Swin Transformer的变体

实验

分类上的实验

目标检测

语义分割

消融实验

点评

---

        Swin Transformer是 ICCV 21的最佳论文，它之所以能有这么大的影响力主要是因为在 ViT 之后，Swin Transformer通过在一系列视觉任务上的强大表现，进一步证明了Transformer是可以在视觉领域取得广泛应用

题目和摘要

        Swin Transformer是一个用了移动窗口的层级式的Vision Transformer

• Swin：来自于 Shifted Windows，Swin Transformer这篇论文的主要贡献
• 层级式 Hierarchical： Swin Transformer像卷积神经网络一样，也能够分成几个 block，做层级式的特征提取，使得提出来的特征有多尺度

        这篇论文提出了一个新的 Vision Transformer 叫做 Swin Transformer，它可以被用来作为一个计算机视觉领域一个通用的骨干网络。

        直接把Transformer用到视觉领域有一些挑战，主要来自于两个方面：

• 多尺度问题：比如一张图片里的代表同样一个语义的词（即物体）有非常不同的尺寸，NLP中没有这个问题。
• 分辨率太大：如果将图片的每一个像素值当作一个token直接输入Transformer，计算量太大。之前的工作要么用后续的特征图来当做Transformer的输入，要么把图片打成 patch 减少这个图片的 resolution，要么把图片画成一个一个的小窗口，然后在窗口里面去做自注意力，所有的这些方法都是为了减少序列长度

        基于这两个挑战，本文提出了 hierarchical Transformer，通过一种叫做移动窗口的方式学习特征，即只在滑动窗口内部计算自注意力，所以称为W-MSA（Window Multi-Self-Attention）。

• 通过Shiting（移动）的操作可以使相邻的两个窗口之间进行交互，也因此上下层之间有了cross-window connection，从而变相达到了全局建模的能力。
• 分层结构使得模型可以提取各个尺度的特征信息
• 计算复杂度与图像大小呈线性关系，这样模型就可以处理更大分辨率的图片（为作者后面提出的Swin V2铺平了道路）。
  • Vision Transformer：进行MSA（多头注意力）计算时，任何一个patch都要与其他所有的patch都进行attention计算，只要窗口大小是固定的，那么计算量与图片的大小成平方增长。
  • Swin Transformer：采用了W-MSA，只对window内部计算MSA，当图片大小增大时，计算量仅仅是呈线性增加。

        因为 Swin Transformer 拥有了像卷积神经网络一样分层的结构，能够提取出多尺度的特征，所以很容易使用到下游任务里。ImageNet-1K 上准确度达到87.3%；在 COCO mAP刷到58.7%（比之前最好的模型提高2.7）；在ADE上语义分割任务也刷到了53.5（提高了3.2个点 ）

        对于 MLP 的架构，用 shift window 的方法也能提升，见MLP Mixer 这篇论文

引言      

ViT在视觉领域应用面临的问题

• ViT 处理的特征都是单一尺寸。ViT把图片打成 patch，patch size 是16*16的，右图中的16×意味着16倍的下采样率，自始至终都是处理的16倍下采样率过后的特征，对多尺寸特征的把握就会弱一些
• 对于密集预测型的任务（检测、分割），有多尺寸的特征至关重要的。
  • 比如目标检测的分层式的卷积神经网络FPN，每一个卷积层出来的特征的 receptive field （感受野）是不一样的，能抓住物体不同尺寸的特征，从而能够很好的处理物体不同尺寸的问题；
  • 物体分割的 UNet，采用 skip connection 的方法，当一系列下采样做完以后，去做上采样的时候，不光是从模型的bottleneck 里去拿特征，还从之前每次下采样的输出中去拿特征，恢复高频率的图像细节

• 检测和分割领域常用的输入尺寸是800*800或者1000*1000，当图片变到这么大的时候，序列长度上千，使用ViT的话，计算复杂度难以承受的

W-MSA 特点和好处

• 使用窗口（Window）的形式将特征图划分成了多个不相交的区域，并且只在每个窗口内进行多头注意力计算，大大减少计算量。
  • 这种设计利用了卷积神经网络里局部性的先验知识。同一个物体的不同部位或者语义相近的不同物体大概率出现在相连的地方，所以在一个小范围的窗口算自注意力是差不多够用的，对于视觉任务来说，全局计算自注意力其实是有点浪费资源的
  • CNN是以滑动窗口的形式一点一点地在图片上进行卷积的，所以假设图片上相邻的区域会有相邻的特征，靠得越近的东西相关性越强。
  • 将每49个patch划分为一个窗口，只在窗口内进行注意力计算，于是序列长度就只有49，解决了计算复杂度的问题。
• 使用patch merging把相邻的小 patch 合成一个大 patch，后者能看到之前四个小patch看到的内容，感受野就增大了，从而抓住多尺寸的特征。
  • 卷积神经网络有多尺寸的特征，主要是因为池化能够增大每一个卷积核能看到的感受野，从而使得每次池化过后的特征抓住物体的不同尺寸。patch merging类似于池化
  • 一旦有了4x、8x、16x的特征图，就可以通过FPN结构做检测，通过UNet结构就可以做分割了。

        这就是作者反复强调的，Swin Transformer是能够当做一个通用的骨干网络的，不光是能做图像分类，还能做密集预测性的任务

移动窗口的操作

        图中每一个灰色的patch 是最基本的元素单元，也就是图一中4*4的patch；每个红色的框是一个中型的计算单元，也就是一个窗口。在本论文里，一个小窗口默认有49个patch。

• 因为Transformer的初衷就是更好的理解上下文，如果窗口都是不重叠的，那自注意力就变成孤立自注意力，没有全局建模的能力
• 加上 shift 的操作，每个 patch就可以在新的窗口里与别的 patch就进行交互，而这个新的窗口里所有的 patch 其实来自于上一层别的窗口里的 patch，这也就是作者说的cross-window connection，即窗口和窗口之间交互

        shift 操作就是往右下角的方向整体移两个 patch，然后在新的特征图里把它再次分成四方格。这样的好处是窗口与窗口之间可以互动。如果不使用shift，那么每次自注意力的操作都在同一个窗口里进行了，每个窗口里的 patch 就永远无法注意到别的窗口里的 patch 的信息，达不到使用 Transformer 的初衷

        patch merging使得到 Transformer 最后几层的时候，每一个 patch 本身的感受野就已经很大了，能看到大部分图片信息，然后再加上移动窗口的操作，窗口内的局部注意力就变相等于全局自注意力操作。既省内存，效果也好

展望

        作者坚信一个 CV 和NLP 之间大一统的框架是能够促进两个领域共同发展的

• Swin Transformer还是利用了一些视觉里的先验知识
• 在模型大一统上，也就是 unified architecture 上来说，其实 ViT 还是做的更好的，因为它什么先验信息都不加，把所有模态的输入直接拼接起来，当成一个很长的输入，直接扔给Transformer去做，而不用考虑每个模态的特性

结论

        这篇论文提出了 Swin Transformer，它是一个层级式的Transformer，计算复杂度是跟输入图像的大小呈线性增长的

        Swin Transformerr 在 COCO 和 ADE20K上的效果远远超越了之前最好的方法，希望 Swin Transformer 能够激发出更多更好的工作，尤其是在多模态方面

        这篇论文里最关键的一个贡献就是基于 Shifted Window 的自注意力，它对很多视觉的任务，尤其是对下游密集预测型的任务是非常有帮助的，但是如果 Shifted Window 操作不能用到 NLP 领域里，其实在模型大一统上论据就不是那么强了，所以作者说接下来他们的未来工作就是要把 Shifted Windows用到 NLP 里面，而且如果真的能做到这一点，那 Swin Transformer真的就是一个里程碑式的工作了，而且模型大一统的故事也就讲的圆满了

方法

模型总览图如下图所示。整个模型采取层次化的设计，一共包含4个Stage，每个stage都会缩小输入特征图的分辨率，像CNN一样逐层扩大感受野。

前向过程

假设输入图片尺寸是224*224*3（ImageNet 标准尺寸）

• patch partition：像 ViT 那样把图片打成 patch，patch size 是4*4，得到图片的尺寸是56*56*48。向量的维度48，因为4*4*3
• Linear Embedding：把向量的维度变成一个超参数c（对于 Swin tiny 网络，c 是96），尺寸就变成了56*56*96，拉直变成3136（56*56）长的序列，96是每一个token向量的维度
  • Patch Partition 和 Linear Embedding相当于是 ViT 里的Patch Projection 操作，而在代码里也是用一次卷积操作就完成了，kernel size=4×4，stride=4，num_kernel=48
  • swin-transformer有T、S、B、L等不同大小，其C的值也不同，比如Swin-Tiny中，C=96
• swin transformer block：将每49个patch划分为一个窗口，只在窗口内计算自注意力。swin transformer block的输入输出尺寸是不变的，所以stage1输出还是56*56*96
• 层级式的 transformer：通过四个Stage构建不同大小的特征图，从而掌握多尺寸的特征信息。后三个stage都是先通过一个Patch Merging层进行2倍的下采样，再通过一些 Swin Transformer block。（[56,56,96]—>[28,28,192]—>[14,14,384]—>[7,7,768]）
  • 特征图的维度很像残差卷积网经，过每个残差阶段之后的特征图大小也是56*56、28*28、14*14，最后是7*7

• 如果是分类任务，后面还会接上一个Layer Norm层、全局池化层以及全连接层得到最终输出。[7,7,768]—>[1,768]—>[1,num_class]
  • 为了和卷积神经网络保持一致，没有像 ViT 一样使用 CLS token，而是对最后的特征图使用global average polling全局池化

        看完整个前向过程之后，就会发现 Swin Transformer 有四个 stage，还有类似于池化的 patch merging 操作，自注意力是在小窗口之内做的，以及最后用 global average polling，所以说 Swin Transformer 这篇论文把卷积神经网络和 Transformer 这两系列的工作完美的结合到了一起，是披着Transformer皮的卷积神经网络

代码框架

class SwinTransformer(nn.Module):
    def __init__(...):
        super().__init__()
        ...
        # absolute position embedding
        if self.ape:
            self.absolute_pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dim))
            
        self.pos_drop = nn.Dropout(p=drop_rate)

        # build layers
        self.layers = nn.ModuleList()
        for i_layer in range(self.num_layers):
            layer = BasicLayer(...)
            self.layers.append(layer)

        self.norm = norm_layer(self.num_features)
        self.avgpool = nn.AdaptiveAvgPool1d(1)
        self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()

    def forward_features(self, x):
        x = self.patch_embed(x)
        if self.ape:
            x = x + self.absolute_pos_embed
        x = self.pos_drop(x)

        for layer in self.layers:
            x = layer(x)

        x = self.norm(x)  # B L C
        x = self.avgpool(x.transpose(1, 2))  # B C 1
        x = torch.flatten(x, 1)
        return x

    def forward(self, x):
        x = self.forward_features(x)
        x = self.head(x)
        return x

其中有几个地方处理方法与ViT不同：

•  ViT在输入会给embedding进行位置编码。而Swin-T这里则是作为一个可选项（self.ape），Swin-T是在计算Attention的时候做了一个相对位置编码
• ViT会单独加上一个可学习参数，作为分类的token。而Swin-T则是直接做平均，输出分类，有点类似CNN最后的全局平均池化层

Patch Embedding：切出patch并做Embedding

        将图片切成一个个patch，然后嵌入向量。具体做法是对原始图片裁成一个个 patch_size * patch_size的窗口大小，然后进行嵌入。

        这里可以通过二维卷积层，将stride，kernel size设置为patch_size大小。设定输出通道来确定嵌入向量的大小。最后将H,W维度展开，并移动到第一维度

class PatchEmbed(nn.Module):
    def __init__(self, img_size=224, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
        super().__init__()
        img_size = to_2tuple(img_size) # -> (img_size, img_size)
        patch_size = to_2tuple(patch_size) # -> (patch_size, patch_size)
        patches_resolution = [img_size[0] // patch_size[0], img_size[1] // patch_size[1]]
        self.img_size = img_size
        self.patch_size = patch_size
        self.patches_resolution = patches_resolution
        self.num_patches = patches_resolution[0] * patches_resolution[1]

        self.in_chans = in_chans
        self.embed_dim = embed_dim

        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
        if norm_layer is not None:
            self.norm = norm_layer(embed_dim)
        else:
            self.norm = None

    def forward(self, x):
        # 假设采取默认参数
        x = self.proj(x) # 出来的是(N, 96, 224/4, 224/4) 
        x = torch.flatten(x, 2) # 把HW维展开，(N, 96, 56*56)
        x = torch.transpose(x, 1, 2)  # 把通道维放到最后 (N, 56*56, 96)
        if self.norm is not None:
            x = self.norm(x)
        return x

Patch Merging：把临近的小 patch合并成一个大 patch

        把临近的小 patch合并成一个大 patch，从而起到下采样一个特征图的效果。图片来自太阳花的小绿豆的博客

        假设输入的是一个4x4大小的单通道特征图（feature map），分割窗口大小为2×2，Patch Merging操作如下：

• 分割：Patch Merging会将每2x2的相邻像素划分为一个patch，然后将每个patch中相同位置（同一颜色）像素拼在一起，得到了4个feature map。如果原张量的维度是 h * w * c，经过这次采样之后就得到了4个张量，每个张量的大小是 h/2、w/2
  • 拼接：将这四个feature map在c 的维度上进行concat拼接。张量的大小就变成了 h/2 * w/2 * 4c，相当于用空间上的维度换了更多的通道数。这个操作，就像卷积神经网络里的池化操作一样
• 归一化：进行LayerNorm处理
  • 改变通道数：为了跟卷积神经网络那边保持一致（一般在池化操作降维之后，通道数都会翻倍），这里也只想让通道数翻倍，所以在 c 的维度上用一个1乘1的卷积，把通道数降成2c。大小为 h*w*c 的张量变成 h/2 * w/2 *2c 的一个张量

        可以看出，通过Patch Merging层后，feature map的高、宽会减半，深度翻倍。具体来说，输出的大小就从56*56*96变成了28*28*192

class PatchMerging(nn.Module):
    def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
        super().__init__()
        self.input_resolution = input_resolution
        self.dim = dim
        self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
        self.norm = norm_layer(4 * dim)

    def forward(self, x):
        """
        x: B, H*W, C
        """
        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"
        assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."

        x = x.view(B, H, W, C)

        x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C  # 从上图中左上角，选取起点后再横向和纵向上分别按照步长2取数
        x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
        x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
        x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
        x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
        x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C

        x = self.norm(x)
        x = self.reduction(x)

       return x

     

划分出包含patch的窗口

        原图片会被平均的分成一些没有重叠的窗口，将原本的张量从 N H W C, 划分成 num_windows*B, window_size, window_size, C，其中 num_windows = H*W / (window_size*window_size)，即窗口的个数。默认每一个小窗口里有7*7个patch。拿第一层之前的输入来举例，它的尺寸就是56*56*96，一共会有8*8=64个窗口，在这64个窗口里分别去算它们的自注意力。window reverse函数则是对应的逆过程。这两个函数会在后面的Window Attention用到。

def window_partition(x, window_size):
    B, H, W, C = x.shape
    x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
    windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
    return windows

def window_reverse(windows, window_size, H, W):
    B = int(windows.shape[0] / (H * W / window_size / window_size))
    x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
    x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
    return x

Window Attention

        这是这篇文章的关键。传统的Transformer都是基于全局来计算注意力的，因此计算复杂度十分高。而Swin Transformer则将注意力的计算限制在每个窗口内，进而减少了计算量。

        主要区别是在原始计算Attention的公式中的Q,K时加入了相对位置编码。其中 Q , V 的形状是 n×d，B 的形状是 n×n ，n是token vector的数目。可以看出，B的作用是给attention map QKT的每个元素加了一个值。其本质就是希望attention map进一步有所偏重。因为attention map中某个值越低，经过softmax之后，该值会更低。对最终特征的贡献就低。后续实验有证明相对位置编码的加入提升了模型性能。

代码

class WindowAttention(nn.Module):   

    def __init__(self, dim, window_size, num_heads, qkv_bias=True, qk_scale=None, attn_drop=0., proj_drop=0.):

        super().__init__()
        self.dim = dim
        self.window_size = window_size  # Wh, Ww
        self.num_heads = num_heads # nH
        head_dim = dim // num_heads # 每个注意力头对应的通道数
        self.scale = qk_scale or head_dim ** -0.5 # qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set

		 # 相关位置编码
		self.relative_position_bias_table = nn.Parameter(
		         torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))  # 设置一个形状为（2*(Wh-1) * 2*(Ww-1), nH）的可学习变量，用于后续的位置编码
		         
		# get pair-wise relative position index for each token inside the window
		 coords_h = torch.arange(self.window_size[0])
		 coords_w = torch.arange(self.window_size[1])
		 coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
		 coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
		 relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
		 relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
		 relative_coords[:, :, 0] += self.window_size[0] - 1  # shift to start from 0
		 relative_coords[:, :, 1] += self.window_size[1] - 1
		 relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
		 relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
		 self.register_buffer("relative_position_index", relative_position_index)
	     # 相关位置编码结束

        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias) # qkv_bias (bool, optional):  If True, add a learnable bias to query, key, value. Default: True
        self.attn_drop = nn.Dropout(attn_drop) # Dropout ratio of attention weight. Default: 0.0
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop) # Dropout ratio of output. Default: 0.0

        trunc_normal_(self.relative_position_bias_table, std=.02)
        self.softmax = nn.Softmax(dim=-1)

Relative Position Bias：相关位置编码       

参考太阳花的小绿豆的博客和图解Swin Transformer - 知乎

        1.初始化relative_position_bias_table

        self.relative_position_bias_table是初始化表，后面的内容就是建立一个可以根据query和key的相对位置查表参数的index。

self.relative_position_bias_table = nn.Parameter(
         torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))  # 2*Wh-1 * 2*Ww-1, nH

        2.计算相对位置索引

        下图蓝色像素，在蓝色像素使用q与所有像素k进行匹配过程中，是以蓝色像素为参考点。然后用蓝色像素的绝对位置索引与其他位置索引进行相减，就得到其他位置相对蓝色像素的相对位置索引，同理可以得到其他位置相对蓝色像素的相对位置索引矩阵（第一排四个位置矩阵）。

        3.将每个相对位置索引矩阵按行展平，并拼接在一起可以得到右下角4x4矩阵。

        利用torch.arange和torch.meshgrid函数生成对应的坐标，这里我们以windowsize=2为例子

coords_h = torch.arange(self.window_size[0])
coords_w = torch.arange(self.window_size[1])
coords = torch.meshgrid([coords_h, coords_w]) # -> 2*(wh, ww)

"""
  (tensor([[0, 0],
           [1, 1]]),
   tensor([[0, 1],
           [0, 1]]))
"""

        然后堆叠起来，展开为一个二维向量

coords = torch.stack(coords)  # 2, Wh, Ww
coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
"""
tensor([[0, 0, 1, 1],
        [0, 1, 0, 1]])
"""

        利用广播机制，分别在第二维，第一维，插入一个维度，进行广播相减，得到 2, wh*ww, wh*ww的张量

relative_coords_first = coords_flatten[:, :, None]  # 2, wh*ww, 1
relative_coords_second = coords_flatten[:, None, :] # 2, 1, wh*ww
relative_coords = relative_coords_first - relative_coords_second # 最终得到 2, wh*ww, wh*ww 形状的张量

        4.索引转换为一维：把二维索引转成一维索引。

        - 得到的索引是从负数开始的，加上偏移量M-1(M为窗口的大小，在本示例中M=2)，让其从0开始。

relative_coords = relative_coords.permute(1, 2, 0).contiguous() # Wh*Ww, Wh*Ww, 2
relative_coords[:, :, 0] += self.window_size[0] - 1
relative_coords[:, :, 1] += self.window_size[1] - 1

        - 将所有的行标都乘上2M-1

        这是因为后续需要将其展开成一维偏移量。而对于(1，2）和（2，1）这两个坐标，在二维上是不同的，但是通过将x,y坐标相加转换为一维偏移的时候，偏移量是相等的。 所以将所有的行标都乘上2M-1，以进行区分

relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1

        - 将行标和列标进行相加。

        最后一维上进行求和，展开成一个一维坐标，并注册为一个不参与网络学习的变量

relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
self.register_buffer("relative_position_index", relative_position_index)

        注意看，主对角线都是4。上三角都是比4小，最低为0；下三角都比4大，且最大为8；一共9个数字，正好等于relative_position_bias_table的宽和高。

        以第一行为例，第一个元素为4，第二个元素为3；对应就是方格图中标号为1和2的位置。

        只要query在key的左边一格，relative_position_index中对应的位置都是3。比如第三行的最后一个数字。观察其他元素之间的位置，可以发现相同的规律。因此，不难得出结论：B中值和query和key的相对位置有关系。相对位置一致的query-key pair，会采用相同的bias。

        5.取出相对位置偏置参数。真正使用到的可训练参数B 是保存在relative position bias table表里的，其长度是等于 (2M−1)×(2M−1)。相对位置偏置参数B，是根据相对位置索引来查relative position bias table表得到的，如下图所示。

        为啥表长是(2M−1)×(2M−1)？考虑两个极端位置，蓝色框的绝对位置为（0,0）时，能取到的相对位置极值为（-1，-1），绿色框的绝对位置为（0,0）时，能取到的相对位置极值为（1，1），即行和列都能取到（2M-1）个数。考虑到所有的排列组合，表的长度就是(2M−1)×(2M−1)

relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
            self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)  # Wh*Ww,Wh*Ww,nH
relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww

前向代码

 def forward(self, x, mask=None):
        """
        Args:
            x: input features with shape of (num_windows*B, N, C)
            mask: (0/-inf) mask with shape of (num_windows, Wh*Ww, Wh*Ww) or None
        """
        B_, N, C = x.shape
        
        qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

        q = q * self.scale
        attn = (q @ k.transpose(-2, -1)) #QK计算出来的Attention张量形状为(numWindows*B, num_heads, window_size*window_size, window_size*window_size)

        relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
            self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)  # Wh*Ww,Wh*Ww,nH
        relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww
        attn = attn + relative_position_bias.unsqueeze(0) # (1, num_heads, windowsize, windowsize)

        if mask is not None: # 下文会分析到
            ...
        else:
            attn = self.softmax(attn)

        attn = self.attn_drop(attn)

        x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

 

W-MSA计算复杂度

        基于窗口的自注意力计算方式能比全局的自注意力方式省多少呢？估计公式如下图所示

• h代表feature map的高度
• w代表feature map的宽度
• C代表feature map的深度
• M代表每个窗口（Windows）的大小

        公式（1）对应的是标准的多头自注意力的计算复杂度。每一个图片有 h*w 个 patch，在刚才的例子里，h 和 w 分别都是56，c 是特征的维度

        以标准的多头自注意力为例。刚开始输入是 h*w*c

• 自注意力首先把它变成 q k v 三个向量：用一个 hw×c 的向量乘以一个 c×c 的系数矩阵，最后得到了 hw×c。每一个计算的复杂度是 hwc^2，因为有三次操作，所以是3hwc^2
• query 和 k相乘 ：hw×c乘以 k 的转置，也就是 c×hw，得到了 hw×hw，这个计算复杂度就是(hw)^2*c
• 自注意力矩阵和value相乘：计算复杂度还是 (hw)^2*c
• 投射层：hw×c乘以 c×c 变成了 hw×c ，计算复杂度就又是 hwc^2

        最后合并起来就是最后的公式（1）

        公式（2）对应的是基于窗口的自注意力计算的复杂度

• 每个窗口里算的还是多头自注意力，可以直接套用公式（1），只不过序列长度只有 M * M 这么大，也就是 hw 变成了 MM
• 把 M 值带入到公式（1）之后，得到一个窗口里多头自注意力计算复杂度是4M^2 * c^2 + 2M^4 * c
• 一共有 h/M * w/M 个窗口，乘以每个窗口所需要的计算复杂度就能得到公式（2）了

        对比公式（1）和公式（2），虽然这两个公式前面这两项是一样的，只有后面从 (h*w)^2变成了 M^2 * h * w，h*w 如果是56*56的话， M^2 其实只有49，所以是相差了几十甚至上百倍的

移动窗口

        W-MSA虽然很好地解决了内存和计算量的问题，但是窗口和窗口之间没有通信，所以作者就提出移动窗口的方式

        与Window Attention不同的地方在于这个模块存在窗口滑动，所以叫做shifted window。滑动距离是window_size//2，方向是右下角。

        如下图所示，左侧是网络第L层使用的W-MSA模块，右侧是第L+1层使用SW-MSA模块。对比可以发现，窗口（Windows）发生了偏移。在L+1层特征图上，第1行第2列的2x4的窗口，能够使第L层的第一行的两个窗口信息进行交流。第二行第二列的4x4的窗口，他能够使第L层的四个窗口信息进行交流，其他同理。

提高移动窗口的计算效率

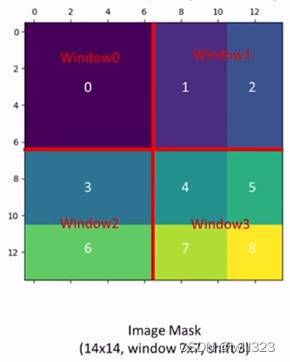
        上面的实现有一个问题：偏移后，窗口数由原来的4个变成了9个，窗口的数量增加了，而且每个窗口里的元素大小不一，无法进行批次处理快速运算MSA。为此，作者提出masked MSA，让Shifted Window Attention在与Window Attention相同的窗口个数下，达到等价的计算结果。

• 先做一次循环移位（ cyclic shift ），A，B，C分别到了新的位置
• 大的特征图上分成四宫格，又得到了4个窗口。
• 出现另一个问题，就是合并的窗口本身是不相邻的，比如A和C，如果直接进行MSA计算，是有问题的。论文中给的方法是Masked MSA，来隔绝不同区域的信息，让每个窗口之间能够合理地计算自注意力。
• 算完了多头自注意力之后，需要把循环位移再还原回去

代码里对特征图移位是通过torch.roll来实现的，下面是示意图

如果需要reverse cyclic shift的话只需把参数shifts设置为对应的正数值。

掩码可视化

        上面左图是已经移位后的状态，每个window中，同颜色的色块属于原来相同的window。我们希望在计算Attention的时候，让具有相同index的QK进行计算，而忽略不同index的QK计算结果。

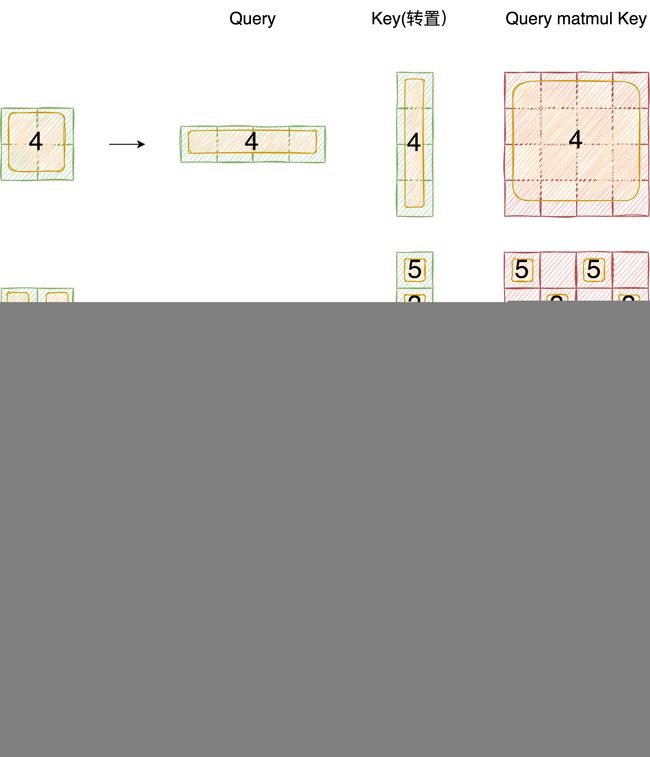
        色块6的长是7，高是3（因为移动window_size//2），色块3的长是7，高是4，把window2拉直以后，得到的向量有49个元素，前28个是色块3的patch，后21个是色块6的patch，向量的另一个维度是C。Q和K的转置相乘，在新矩阵中，属于同一个色块做自注意力的结果是右图中黄色的部分（见window2），掩码设为0，否则是棕色的部分，掩码为-100。自注意力的结果加上掩码，送入softmax，就把棕色的部分遮盖住了。

        对于window1，拉直以后得到的向量中色块1和色块2的元素交错，所以得到围棋形状的矩阵

以下来自图解Swin Transformer - 知乎

        首先我们对Shift Window后的每个窗口都给上index，并且做一个roll操作（window_size=2, shift_size=-1）

        正确的结果如下图所示 (PS: 这个图的Query Key画反了，应该是4x1 和 1x4 做矩阵乘）

        要想在原始四个窗口下得到正确的结果，我们就必须给Attention的结果加入一个mask（如上图最右边所示）

代码  

if self.shift_size > 0:
            # calculate attention mask for SW-MSA
            H, W = self.input_resolution
            img_mask = torch.zeros((1, H, W, 1))  # 1 H W 1
            h_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            w_slices = (slice(0, -self.window_size),
                        slice(-self.window_size, -self.shift_size),
                        slice(-self.shift_size, None))
            cnt = 0
            for h in h_slices:
                for w in w_slices:
                    img_mask[:, h, w, :] = cnt
                    cnt += 1

            mask_windows = window_partition(img_mask, self.window_size)  # nW, window_size, window_size, 1
            mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
            attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
            attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(attn_mask == 0, float(0.0))

以上图的设置，我们用这段代码会得到这样的一个mask

tensor([[[[[   0.,    0.,    0.,    0.],
           [   0.,    0.,    0.,    0.],
           [   0.,    0.,    0.,    0.],
           [   0.,    0.,    0.,    0.]]],

[[[   0., -100.,    0., -100.],
           [-100.,    0., -100.,    0.],
           [   0., -100.,    0., -100.],
           [-100.,    0., -100.,    0.]]],

[[[   0.,    0., -100., -100.],
           [   0.,    0., -100., -100.],
           [-100., -100.,    0.,    0.],
           [-100., -100.,    0.,    0.]]],

[[[   0., -100., -100., -100.],
           [-100.,    0., -100., -100.],
           [-100., -100.,    0., -100.],
           [-100., -100., -100.,    0.]]]]])

        在之前的window attention模块的前向代码里，包含这么一段

 if mask is not None:
            nW = mask.shape[0]
            attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
            attn = attn.view(-1, self.num_heads, N, N)
            attn = self.softmax(attn)

        将mask加到attention的计算结果，并进行softmax。mask的值设置为-100，softmax后就会忽略掉对应的值

        作者通过这种巧妙的循环位移的方式和巧妙设计的掩码模板，从而实现了只需要一次前向过程，就能把所有需要的自注意力值都算出来，而且只需要计算4个窗口，也就是说窗口的数量没有增加，计算复杂度也没有增加，非常高效的完成了这个任务

Transformer Block整体架构

如果先是 window多头自注意力再是 shifted window 多头自注意力的话，就能起到窗口和窗口之间互相通信的目的了，所以在 Swin Transformer里，每次都是先做一次基于窗口的多头自注意力，然后再做一次基于移动窗口的多头自注意力。如下图所示

• 每次输入先进来之后先做一次 Layernorm，然后做窗口的多头自注意力，然后再过 Layernorm 过 MLP，第一个 block 就结束了
• 这个 block 结束以后，紧接着做一次基于移动窗口的多头自注意力，然后再过 MLP 得到输出

        这两个 block 加起来其实才算是 Swin Transformer 一个基本的计算单元，这也就是为什么stage1、2、3、4中的 swin transformer block 层数总是偶数

Block的前向代码   

 def forward(self, x):
        H, W = self.input_resolution
        B, L, C = x.shape
        assert L == H * W, "input feature has wrong size"

        shortcut = x
        x = self.norm1(x)
        x = x.view(B, H, W, C)

        # cyclic shift
        if self.shift_size > 0:
            shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
        else:
            shifted_x = x

        # partition windows
        x_windows = window_partition(shifted_x, self.window_size)  # nW*B, window_size, window_size, C
        x_windows = x_windows.view(-1, self.window_size * self.window_size, C)  # nW*B, window_size*window_size, C

        # W-MSA/SW-MSA
        attn_windows = self.attn(x_windows, mask=self.attn_mask)  # nW*B, window_size*window_size, C

        # merge windows
        attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
        shifted_x = window_reverse(attn_windows, self.window_size, H, W)  # B H' W' C

        # reverse cyclic shift
        if self.shift_size > 0:
            x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
        else:
            x = shifted_x
        x = x.view(B, H * W, C)

        # FFN
        x = shortcut + self.drop_path(x)
        x = x + self.drop_path(self.mlp(self.norm2(x)))

return x

整体流程如下

• 先对特征图进行LayerNorm
• 通过self.shift_size决定是否需要对特征图进行shift
• 然后将特征图切成一个个窗口
• 计算Attention，通过self.attn_mask来区分Window Attention还是Shift Window Attention
• 将各个窗口合并回来
• 如果之前有做shift操作，此时进行reverse shift，把之前的shift操作恢复
• 做dropout和残差连接
• 再通过一层LayerNorm+全连接层，以及dropout和残差连接

       

        到此，Swin Transformer整体的故事和结构就已经讲完了，主要的研究动机就是想要有一个层级式的 Transformer，为了这个层级式，所以介绍了 Patch Merging 的操作，从而能像卷积神经网络一样把 Transformer 分成几个阶段，为了减少计算复杂度，争取能做视觉里密集预测的任务，所以又提出了基于窗口和移动窗口的自注意力方式，也就是连在一起的两个Transformer block，最后把这些部分加在一起，就是 Swin Transformer 的结构

Swin Transformer的变体

• Swin Tiny: C = 96, layer numbers = {2, 2, 6, 2}
• Swin Small: C = 96, layer numbers ={2, 2, 18, 2}
• Swin Base: C = 128, layer numbers ={2, 2, 18, 2}
• Swin Large: C = 192, layer numbers ={2, 2, 18, 2}

        Swin Tiny的计算复杂度跟 ResNet-50 差不多，Swin Small 的复杂度跟 ResNet-101 是差不多的，这样主要是想去做一个比较公平的对比

        这里其实就跟残差网络就非常像了，残差网络也是分成了四个 stage，每个 stage 有不同数量的残差块

实验

分类上的实验

两种预训练的方式：不论是用ImageNet-1K去做预训练，还是用ImageNet-22K去做预训练，最后测试的结果都是在ImageNet-1K的测试集上去做的，结果如下表所示

        上半部分是ImageNet-1K预训练的模型结果，跟之前最好的卷积神经网络做了一下对比。

• RegNet 是之前 facebook 用 NAS 搜出来的模型，EfficientNet 是 google 用NAS 搜出来的模型，这两个都算之前表现非常好的模型了，他们的性能最高会到 84.3
• 对于 ViT 来说，因为它没有用很好的数据增强，而且缺少偏置归纳，所以说它的结果是比较差的，只有70多
• 换上 DeiT 之后，因为用了更好的数据增强和模型蒸馏，所以说 DeiT Base 模型也能取得相当不错的结果，能到83.1
• Swin Base 最高能到84.5，稍微比之前最好的卷积神经网络高一点点，就比84.3高了0.2
• 虽然之前表现最好的 EfficientNet 的模型是在 600*600 的图片上做的，而 Swin Base 是在 384*384 的图片上做的，所以说 EfficientNet 有一些优势，但是从模型的参数和计算的 FLOPs 上来说 EfficientNet 只有66M，而且只用了 37G 的 FLOPs，但是 Swin Transformer 用了 88M 的模型参数，而且用了 47G 的 FLOPs，所以总体而言是伯仲之间

        下半部分是用 ImageNet-22k 去做预训练，然后再在ImageNet-1k上微调最后得到的结果

• 一旦使用了更大规模的数据集， ViT 的性能也就已经上来了， ViT large得到 85.2 的准确度
•  Swin Large 更高，能到87.3，这个是在不使用JFT-300M，就是特别大规模数据集上得到的结果，所以还是相当高的 

目标检测

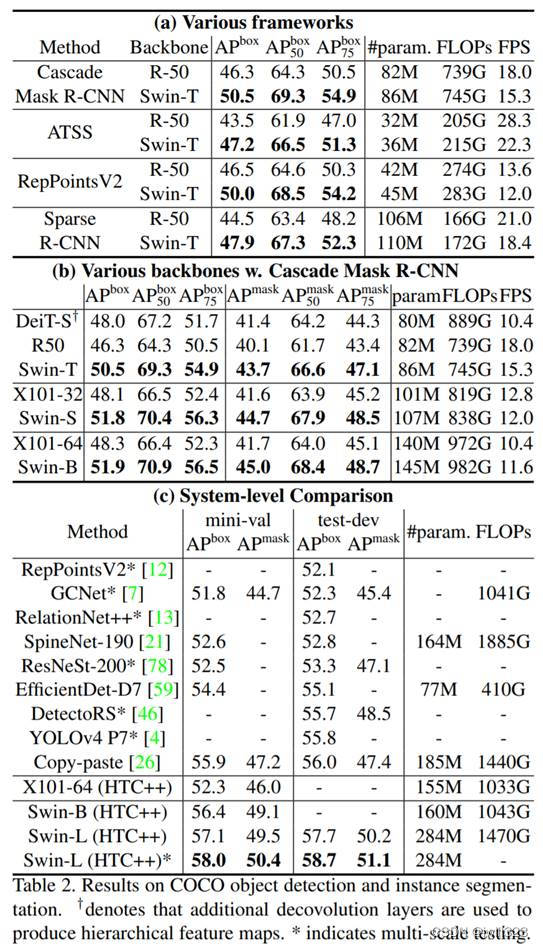
在 COCO 数据集上训练并且进行测试的，结果如下图所示

        表2（a）中测试了在不同的算法框架下，Swin Transformer 到底比卷积神经网络要好多少，主要是想证明 Swin Transformer 是可以当做一个通用的骨干网络来使用的，所以用了 Mask R-CNN、ATSS、RepPointsV2 和SparseR-CNN，在这些算法里，过去的骨干网络选用的都是 ResNet-50，现在替换成了 Swin Tiny

• Swin Tiny 的参数量和 FLOPs 跟 ResNet-50 是比较一致的，所以他们之间的比较是相对比较公平的
• Swin Tiny 对 ResNet-50 是全方位的碾压，在四个算法上都超过了它，而且超过的幅度也是比较大的

        选定了Cascade Mask R-CNN 这个算法，然后换更多的不同的骨干网络，比如 DeiT-S、ResNet-50 和 ResNet-101，也分了几组，结果如上图中表2（b）所示。

•         可以看出，在相似的模型参数和相似的 Flops 之下，Swin Transformer 都是比之前的骨干网络要表现好的

        如上图中的表2（c）所示，就是系统层面的比较，追求的不是公平比较，什么方法都可以上，可以使用更多的数据，可以使用更多的数据增强，甚至可以在测试的使用 test time augmentation（TTA）的方式

•         可以看到，之前最好的方法 Copy-paste 在 COCO Validation Set上的结果是55.9，在 Test Set 上的结果是56，Swin Transformer--Swin Large 的结果分别能达到58和58.7，都比之前高了两到三个点

语义分割

ADE20K数据集，结果如下图所示

• 一直到 DeepLab V3、ResNet 其实都用的是卷积神经网络，之前的这些方法其实都在44、45左右徘徊
• SETR 、用了 ViT Large，取得了50.3的这个结果
• Swin Transformer Large也取得了53.5的结果，更高了
• 其实作者这里也有标注，就是有两个“+”号的，意思是说这些模型是在ImageNet-22K 数据集上做预训练，所以结果才这么好

消融实验

实验结果如下图所示

        表4主要就是想说一下移动窗口以及相对位置编码到底对 Swin Transformer 有多有用

• 可以看到，如果光分类任务的话，其实不论是移动窗口，还是相对位置编码，相对于基线来说，提升没有特别明显，当然在ImageNet的这个数据集上提升一个点也算是很显著了
• 更大的帮助，主要是出现在下游任务里，就是 COCO 和 ADE20K 这两个数据集上，也就是目标检测和语义分割这两个任务上
• 用了移动窗口和相对位置编码以后，都会比之前大概高了3个点左右，提升是非常显著的。这也是合理的，因为密集型预测任务的特征对位置信息更敏感，而且更需要周围的上下文关系，所以说通过移动窗口提供的窗口和窗口之间的互相通信，以及在每个 Transformer block都做更准确的相对位置编码，肯定是会对这类型的下游任务大有帮助的

点评

        除了作者团队自己在过去半年中刷了那么多的任务，比如说最开始讲的自监督的Swin Transformer，还有 Video Swin Transformer 以及Swin MLP，同时 Swin Transformer 还被别的研究者用到了不同的领域

        所以说，Swin Transformer在视觉领域大杀四方，感觉以后每个任务都逃不了跟 Swin 比一比，而且因为 Swin 这么火，所以说其实很多开源包里都有 Swin 的实现

• 百度的 PaddlePaddle
• 视觉里现在比较火的 pytorch-image-models，就是 Timm 这个代码库里面也是有 Swin 的实现的
• Hugging Face 估计也是有的

        Swin Transformer的影响力远远不止于此。本论文对卷积神经网络，对 Transformer，还有对 MLP 这几种架构深入的理解和分析是可以给更多的研究者带来思考的，从而不仅可以在视觉领域里激发出更好的工作，而且在多模态领域里，相信它也能激发出更多更好的工作