AI入门笔记——感知机

概念：

 

有时候，我们需要分类一些东西，如分别一副图像是不是人脸，分辨一段波形是否为“拍照”，这些数据很多时候有无数变量，即无数维，要通过人脑建模对其进行分辨是非常困难的。因此，才有了感知机模型，以极度精简而粗糙的方式模拟神经网络学习的过程——实际上，就是参数调整的过程。

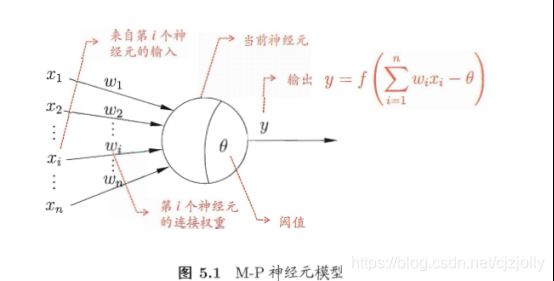
神经细胞可以理解为这样的一个模型：

 

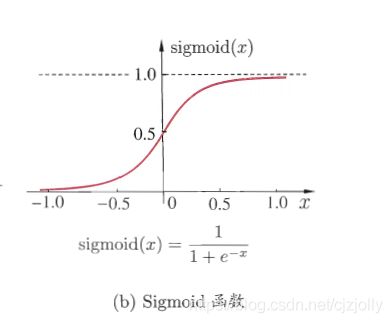
无数的不同强度的“神经脉冲”通过突触输入到“细胞”中，如果累积的强度超过阈值，就从自己的“树突”中进行输出，否则则不输出。神经脉冲的波形可以抽象化为如下Sigmoid函数：

 

这里的“神经脉冲”可以抽象为一系列的输入（X1, X2 …… Xn），而“突触连接强弱程度”可以理解为每个输入对应的权重(W1，W2……Wn)，用于确定其对应的输入信号在被细胞所接收的强弱程度，即(W1*X1，W2*X2……Wn*Xn)，随后求和别输入到Sigmoid中，从而得到[0,1]范围的输出脉冲结果。

 

 

• 应用

现在大家一定很好奇这么个东西有什么用？那现在就用一个简单的例子来展示一下，就是让其自动实现“逻辑与”关系的建立。

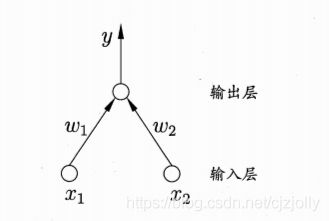
首先我们定义一个模型：

 

这个模型分别有两个输入x1,x2，分别对应两个二进制输入变量，以及对应的权值w1,w2，输出结点有偏移值b = -1，现在我把w1,w2赋予随机数0.537372和-0.359797，此时分别输入[0,0] [0, 1] [1,0] [1,1]作为x1,x2，分别乘以权值w1,w2，求和后输入sigmoid函数，结果得到的脉冲数值分别为：

0.119203

0.086290

0.188066

0.139143

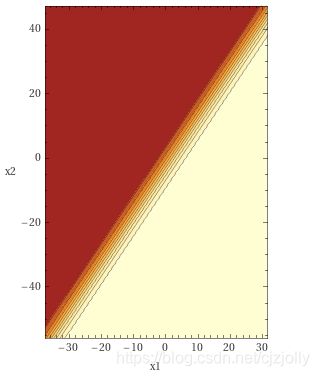
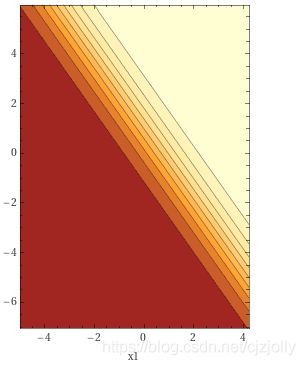
通过图像（颜色越浅值越大），我们也可以发现其分类方式实际有误，所有的输入的输出都在低数值区：

 

这可与预期结果[0, 0, 0, 1]差距深远，怎么办呢？

其实不难发现，基于sigmoid输出值和输入值的关系，我们可以通过调整权重的大小，来缩小脉冲输出和期望输出之间的差距。就像y=kx通过提高k值提高每个x对应y值的大小，而我们现在就是为了寻找合适的k值。

但因为激发函数Sigmoid不是y=kx，所以现在，我们要把误差作为指导，去通过夹逼方式修改对x1,x2两个脉冲的强弱接受度——即权重，来接近我们的期望输出，现在我们可以设脉冲输出为Yout，我们期望的输出为Ys，e为学习率——即夹逼过程的步进速率，我们可以得到dW = e * (Ys - Yout) * X1，即得到本次W1的更新量dW，此时通过W1 = W1 + dW，即完成了W1的一次步进更新，当dW接近或等于0时，代表输出Yout和预期Ys已经非常接近，即W1已经找到合适的权值使得实际输出与目标输出符合了。

 

迭代200次后，权值W1,W2被更新为1.460147，1.031295，可以从函数sigmoid(1.460147*x1+1.031295*x2-1)图像中发现，我们实现了与关系的分类，只有x1 = 1，x2 = 1在高亮度区域上：

 

• 总结

为何这么简单的问题要用如此复杂的方式解决？其实只是为了通过一个简单的例子说明，感知机是一种可以让机器自动根据输入输出对找到线性关系的方式，从而减轻人类负担的一种数学方法，也是BP神经网络等可以找到非线性关系的数学方法的基础。

 

 

 

 

实现代码

package com.cjz.lab.AILab;

import java.util.Random;



public class SensorMachine {
	
	private static int input[][] = {{0, 0}, {0, 1}, {1, 0}, {1, 1}};
	private static double standardOutput[] = {0, 0, 0, 1};
	private static Random random = new Random(100000);  //主要是对权值采取的是随机产生的方法
	private static float etta = 0.02f; //学习率
	
	public static void main(String args[]) {
		Layer inputLayer = new Layer(2, 2);
		Layer outputLayer = new Layer(2, 1);
		
		for(int count = 0; count < 8000; count ++) {
			System.out.println(String.format("weight[0] = %f, weight[1] = %f", outputLayer.mCell[0].mWeight[0], outputLayer.mCell[0].mWeight[1]));
			double inputLayerResult[][] = new double[4][2];
			double outputLayerResult[] = new double[4];
			//forward
			for(int i = 0; i < input.length; i++) {
				inputLayer.input(new double[] {input[i][0], input[i][1]});
				outputLayer.input(inputLayer);
				inputLayerResult[i][0] = inputLayer.mCell[0].result;
				inputLayerResult[i][1] = inputLayer.mCell[1].result;
				outputLayerResult[i] = outputLayer.mCell[0].result;
				//System.out.println("rr:" + String.format("%.6f", outputLayer.mCell[0].result));  //得出结果
			}
			//traning
			for(int i = 0; i < standardOutput.length; i++) {
				outputLayer.mCell[0].mWeight[0] += etta * (standardOutput[i] - outputLayerResult[i]) * input[i][0];
				outputLayer.mCell[0].mWeight[1] += etta * (standardOutput[i] - outputLayerResult[i]) * input[i][1];
				
				//????:
				inputLayer.mCell[0].mWeight[0] += etta * (standardOutput[i] - inputLayerResult[i][0]) * input[i][0];
				inputLayer.mCell[0].mWeight[1] += etta * (standardOutput[i] - inputLayerResult[i][0]) * input[i][0];
				
				inputLayer.mCell[1].mWeight[0] += etta * (standardOutput[i] - inputLayerResult[i][1]) * input[i][0];
				inputLayer.mCell[1].mWeight[1] += etta * (standardOutput[i] - inputLayerResult[i][1]) * input[i][0];
			}
		}
		
		for(int i = 0; i < input.length; i++) {
			outputLayer.input(new double[] {input[i][0], input[i][1]});
			System.out.println("rr:" + String.format("%.6f", outputLayer.mCell[0].result));  //得出结果
		}
	}
	
	private static class Layer {
		public int mCellCount;
		public int mInputCount;
		public double mInputVal[];
		public Cell mCell[];
		
		public Layer(int inputCount, int cellCount) {
			this.mInputCount = inputCount;
			this.mCellCount = cellCount;
			this.mCell = new Cell[cellCount];
			for (int i = 0; i < this.mCell.length; i++) {
				this.mCell[i] = new Cell(inputCount);
			}
		}
		
		public Cell getCell(int index) {
			return mCell[index];
		}
		
		public void input (double inputVal[]) {
			mInputVal = inputVal.clone();
			double sum = 0;
			for (int i = 0; i < this.mCellCount; i++) {
				for (int j = 0; j < inputVal.length; j++) {
					sum += inputVal[j] * this.mCell[i].mWeight[j] + this.mCell[i].mBias; 
				}
				this.mCell[i].result = sigmoid(sum);
				sum = 0;
			}
		}
		
		public void input (Layer prevLayer) {
			mInputVal = new double[prevLayer.mCell.length];
			for (int i = 0; i < prevLayer.mCellCount; i++) {
				mInputVal[i] = prevLayer.mCell[i].result;
			}
			double sum = 0;
			for (int i = 0; i < this.mCellCount; i++) {
				for (int j = 0; j < prevLayer.mCellCount; j++) {
					sum += prevLayer.mCell[j].result * this.mCell[i].mWeight[j] + this.mCell[i].mBias; 
				}
				this.mCell[i].result = sigmoid(sum);
				sum = 0;
			}
		}
	}
	
	private static class Cell {
		
		public double mWeight[];
		public double mBias; 
		public double result;
		
		public Cell(int weightCount) {
			mWeight = new double[weightCount];
			//记得赋随机数给他们
			for (int i = 0; i < weightCount; i++) {
				double real = random.nextDouble();    //随机分配着产生0-1之间的值
	            mWeight[i] = random.nextDouble() > 0.5f ? real : -real;
			}
			mBias = -1f;
		}
	}
	
	public static double sigmoid(double x) {
		return 1 / (1 + Math.exp(-x));
	}

}