Distributed physics informed neural network for data-efficient solution to PDE

论文信息

题目：Distributed physics informed neural network for data-efficient solution to partial differential equations

作者：Vikas Dwivedia,∗, Nishant Parasharb, Balaji Srinivasana

基础补充

内容

动机

动机：

• 传统it is a well-known fact that mesh generation is a very difficult task with complex geometries. Furthermore, the discretisation of the PDE itself introduces
  truncation errors, which can be a quite serious problem
• 对于单个PINN在整个域上表示复杂函数很困难

PINN的缺陷：

• PINNs在表示较宽计算域内的急剧局部梯度时不够稳健
• 要求PINN的深度随着PDE阶数的增加而增加，由于众所周知的消失梯度问题，导致学习速率变慢，
  方法：
  受有限体积方法的灵感，考虑将求解域分成多个cell，在每个cell建立一个PINN，不同cell之间加一个连续与可微约束。具体表示：
  考虑下面的一维非定常问题
  $$\begin{array}{c}\frac{\partial }{\partial t}u(x,t)+\mathcal{N}u(x,t)=R(x,t),(x,t)\in \Omega \\ u(x,t)=B(x,t),(x,t)ϵ\partial \Omega \\ u(x,0)=F(x),xϵ\left[x_L,x_R\right]\end{array}$$
  其中，矩形域$\Omega =\left[x_L,x_R\right]\mathrm{x}[0,T]$，统一将$\Omega$分程不重叠的矩形cell。
  $$\Omega =\bigcup _{i=1}^{N_c}{\Omega }_i$$
  每个cell${\Omega }_i$的边界表示为$\partial {\Omega }_i$，对于矩形区域
  $$\partial {\Omega }_i=\bigcup _{m=1}^4{I}_m^{(i)}$$
  其中，$I_m^{(i)}$表示${\Omega }_i$第$m^{th}$界面
  
  
  第i个cell表示为$M^{(i)}$，每个$M^{(i)}$输出为$f^{(i)}$，对于每个$M^{(i)}$，附加一个额外连续（或光滑）的限制。例如，对于平流问题，解的连续性是充分的。对于扩散问题，解应该是连续可微的。每个神经网络损失:
  $$J=J_{PDE}+J_{BC}+J_{IC}+J_{\text{interface}}$$
  前三个与传统PINN相同，最后一个loss
  $$J_{PDE}=\sum \frac{{\xi }_f^{(i{)}^T{\xi }_f}(i)}{2N_f^{(i)}}$$
  $$J_{BC}=\sum \frac{{\xi }_{bc}^{(j)}{\xi }_{bc}^{(j)}}{2N_{bc}^{(j)}}+\sum \frac{{\xi }_{bc}^{(k{)}^T}{\xi }_{bc}^{(k)}}{2N_{bc}^{(k)}}$$
  $$J_{IC}=\sum \frac{{\xi }_{ic}^{(l)}{\xi }_{ic}^{(l)}}{2N_{ic}^{(l)}}$$
  其中，${\xi }_f^{(i)}={\left(\frac{\partial f^{(i)}}{\partial t}+\mathcal{L}{f}^{(i)}-R^{(i)}\right)}_{{\Omega }_i},{\xi }_{bc}^{(j)}={\left(f^{(j)}-B^{(j)}\right)}_{I_4},{\xi }_{bc}^{(k)}={\left(f^{(k)}-B^{(k)}\right)}_{I_2}，{\xi }_{ic}^{(l)}={\left(f^{(l)}-B^{(l)}\right)}_{I_1}$

$i=\left[1,2,\dots ,N_c\right],j=\left[1,\left(1+N{B}_x\right),\dots ,\left(1+\left(N{B}_t-1\right)N{B}_x\right)\right],k=\left[N{B}_x,2N{B}_x,\dots ,N{B}_t\times N{B}_x\right]，l=\left[1,2,\dots ,N{B}_x\right]$
最后一项$J_{\text{interface}}$作为连续性损失和可微性损失
$J_{\text{interface}}=J_{C_x^0}+J_{C_t^0}+J_{C_2}$
$J_{C_x^0},J_{C_t^0}$对应x,t的连续损失，$J_{C_x^1}$对应着微分损失，

$$J_{C_x^0}=\sum \frac{{\xi }_{C_x^0}^{(i{)}^T{\xi }_{C_x^0}}}{2N_{C^0}^{(i)}}$$
$$\begin{array}{rl}{J}_{C_t^0}& =\sum \frac{{\xi }_{C_t^0}^{(i{)}^T{\xi }_{C_t^0}}}{2N_{C^0}^{(i)}}\\ J_{C_x^1}& =\sum \frac{{\xi }_{C_x^1}^{(i{)}^T{\xi }_{C_x^1}}}{2N_{C_x^1}^{(i)}},\end{array}$$

其中

实验

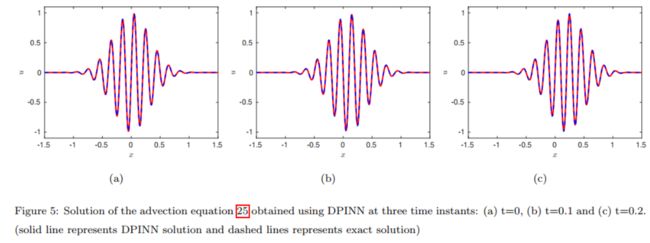
Advection equation

PINN对于这种类型的复杂表示，我们需要在梯度较大的区域中使用大量的训练数据，然而，这些信息是我们先天不知道的，传统PINN的代价函数作为一个正则化器，但仅在全局意义上。因此，该算法很难在较宽的计算范围内捕获这些明显的局部变化，然而，使用更深层次的网络可能会限制训练速度，因为一个众所周知的问题是梯度消失。DPINN在每个cell上采相同数量的点，比起传统PINN随机采点更能获取更多信息，每个cell上使用更简单的MLP

Burgers’ equation

结论

在本文中，我们提出了DPINN -一个数据高效的分布式版本的PINN，以解决线性和非线性偏微分方程。该算法通过改进网络结构和学习算法，提高了PINN的性能。DPINN通过将计算域划分为更小的子域，结合了一种类似于有限体积方法的分治型策略(称为单元)，并在每个单元中构建PINN。这种划分将可能需要非常深的PINN的困难问题分解为更小的子问题，这些子问题可以通过各种最小大小的局部PINN来解决。接口上附加的物理约束充当自然的网络正则化器，提高了网络的表示能力。DPINN本身的代价函数将单个的局部PINN解stitches起来，使得DPINN比原始PINN更具数据效率。

不足

不懂

可借鉴地方